Содержание
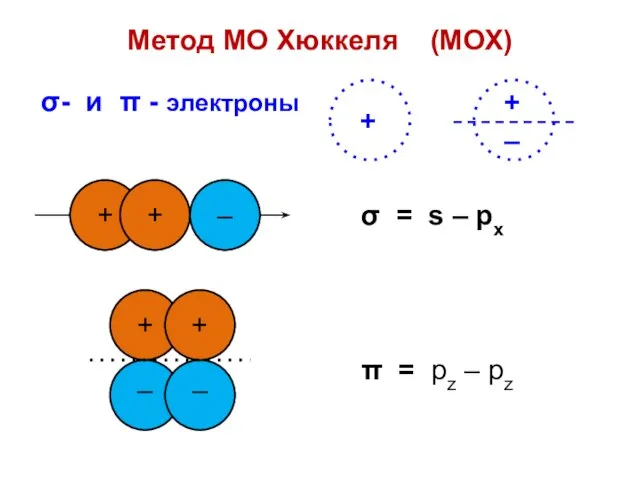
- 2. σ- и π - электроны Метод МО Хюккеля (МОХ)
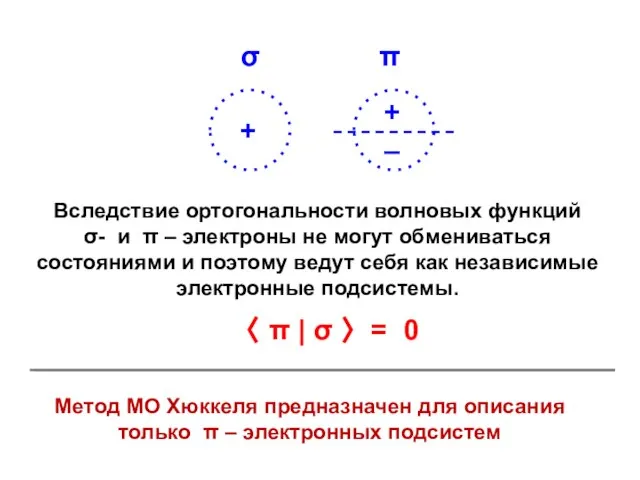
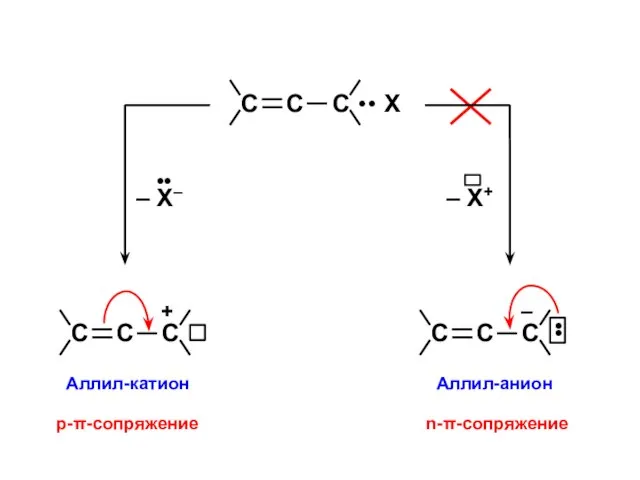
- 3. σ π Вследствие ортогональности волновых функций σ- и π – электроны не могут обмениваться состояниями и
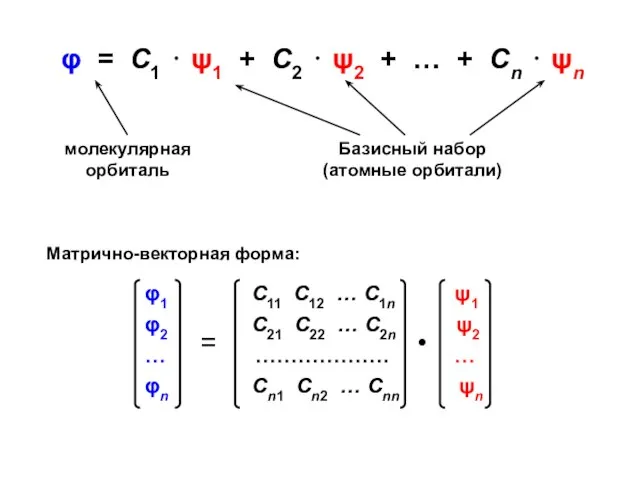
- 5. φ = С1 ⋅ ψ1 + С2 ⋅ ψ2 + … + Сn ⋅ ψn
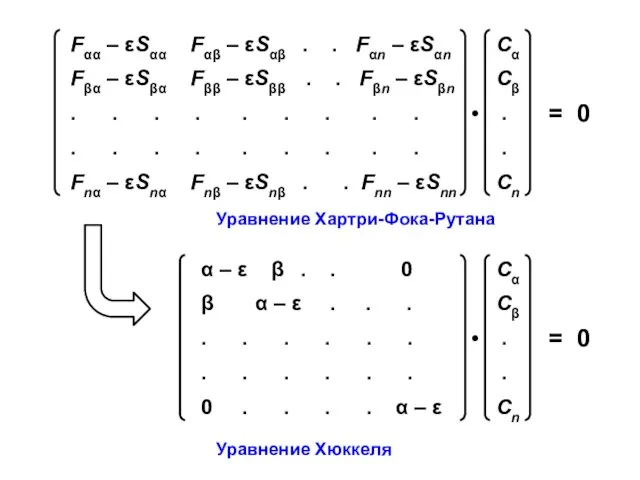
- 6. Уравнения Хартри-Фока-Рутана Fμν — матричные элементы оператора Фока, характеризующие либо энергию электрона в изолированном атоме с
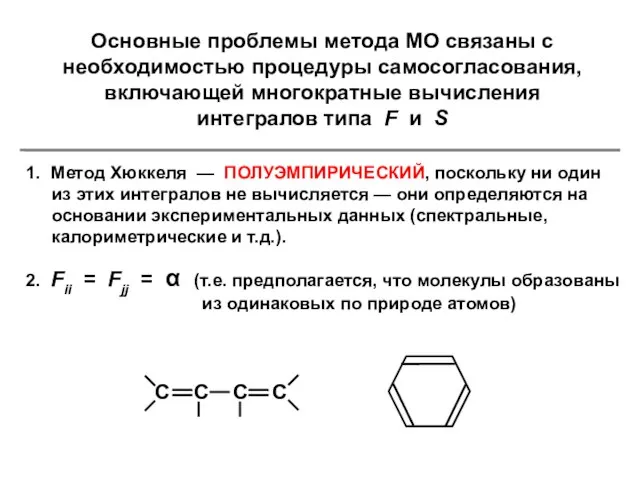
- 7. Основные проблемы метода МО связаны с необходимостью процедуры самосогласования, включающей многократные вычисления интегралов типа F и
- 8. Разделение недиагональных интегралов Fij на два типа (нулевые и ненулевые) осуществляется исключительно на химической основе —
- 9. Уравнение Хартри-Фока-Рутана Уравнение Хюккеля
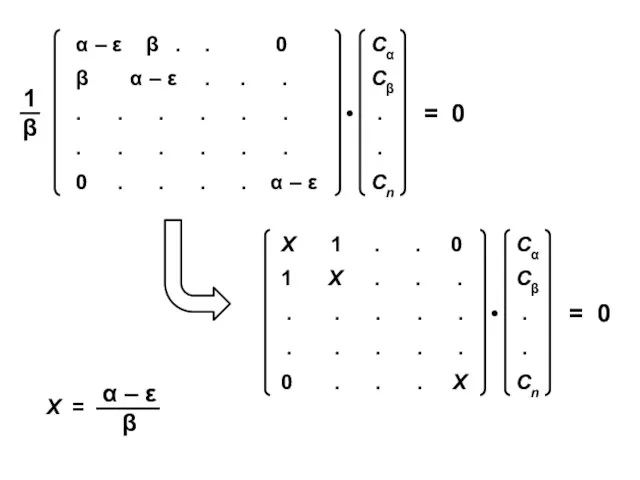
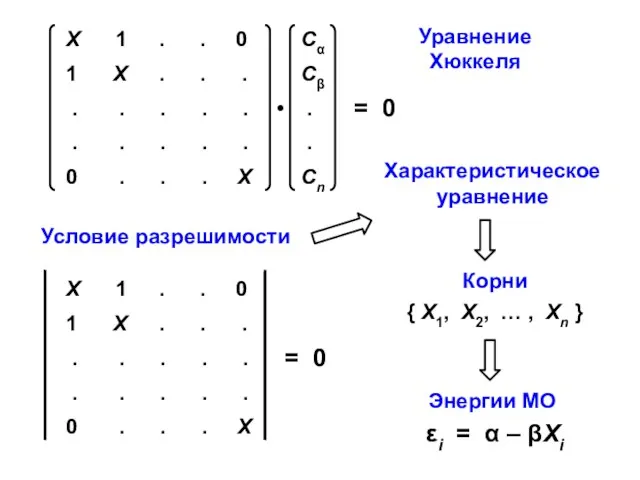
- 11. Уравнение Хюккеля
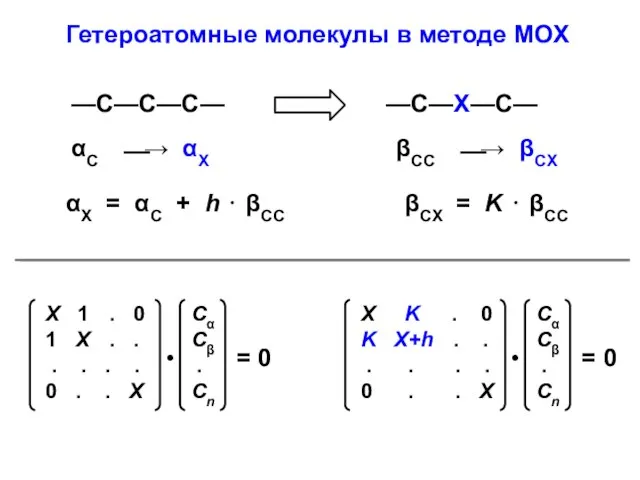
- 12. Гетероатомные молекулы в методе МОХ —С—С—С— αС ⎯→ αX βCC ⎯→ βCX αX = αС +
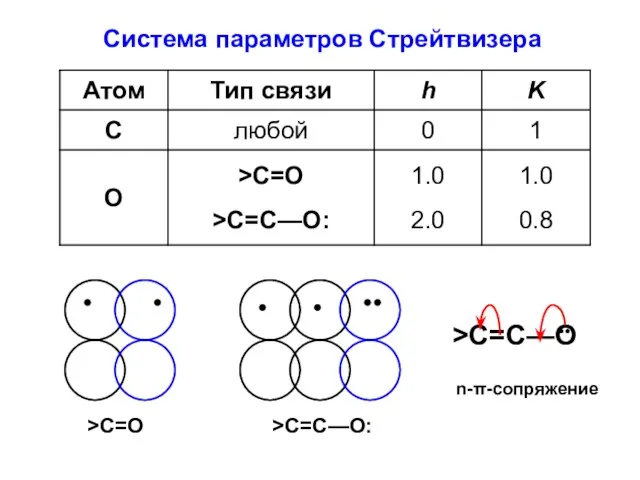
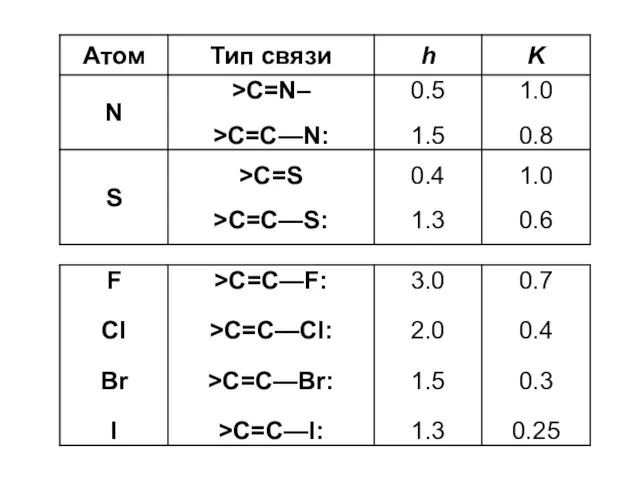
- 13. Система параметров Стрейтвизера
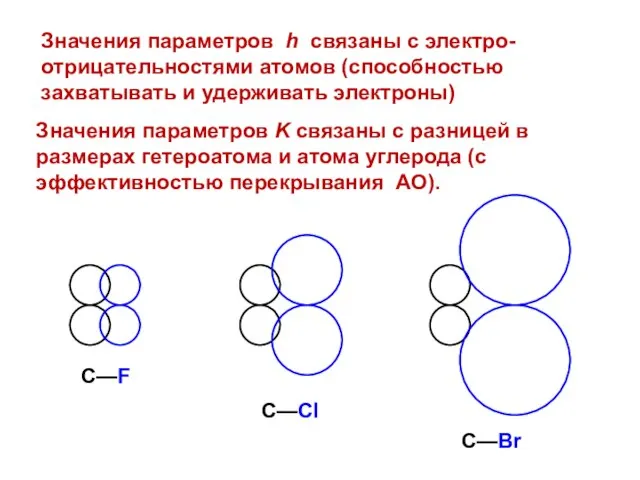
- 15. Значения параметров K связаны с разницей в размерах гетероатома и атома углерода (с эффективностью перекрывания АО).
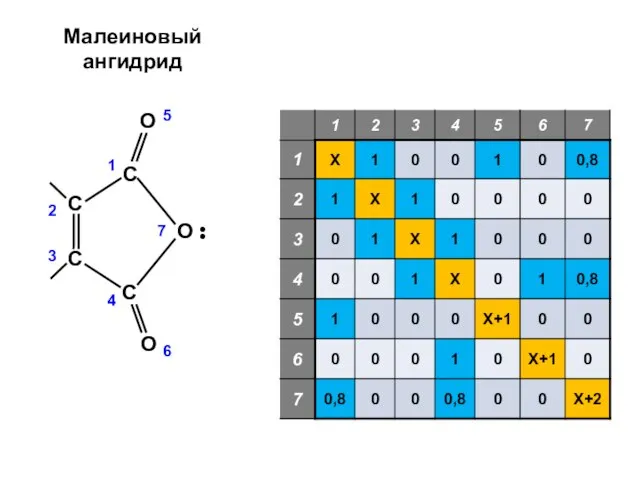
- 16. Малеиновый ангидрид
- 17. Домашнее задание
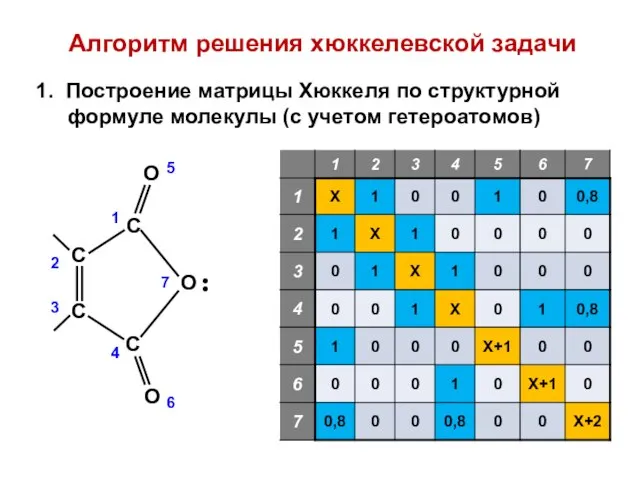
- 18. Алгоритм решения хюккелевской задачи 1. Построение матрицы Хюккеля по структурной формуле молекулы (с учетом гетероатомов)
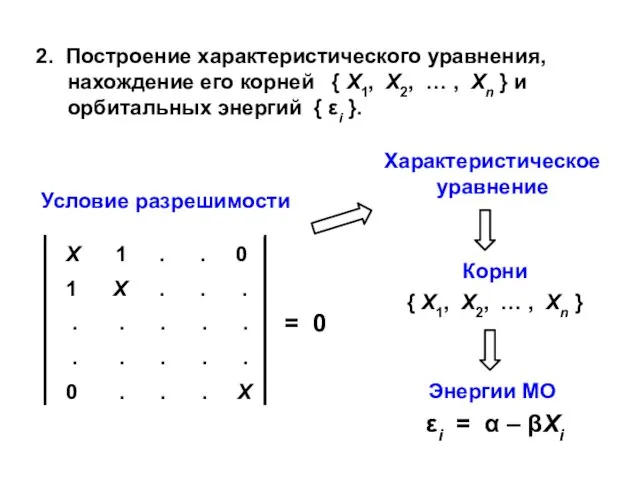
- 19. 2. Построение характеристического уравнения, нахождение его корней { X1, X2, … , Xn } и орбитальных
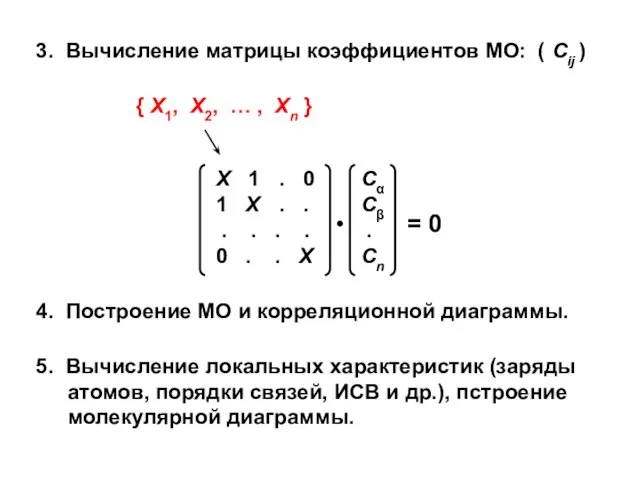
- 20. 3. Вычисление матрицы коэффициентов МО: ( Сij ) 4. Построение МО и корреляционной диаграммы. 5. Вычисление
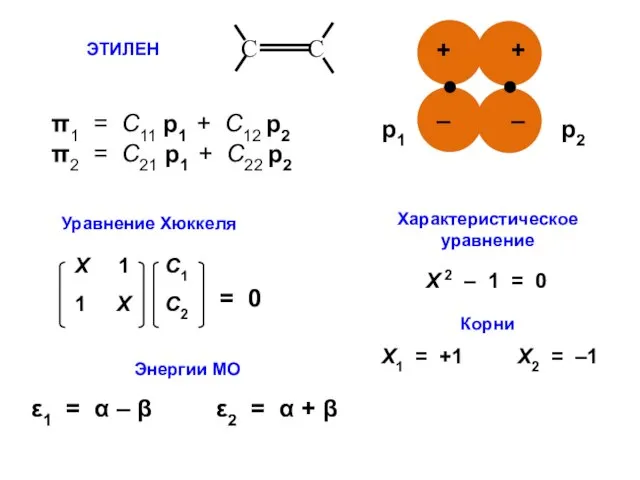
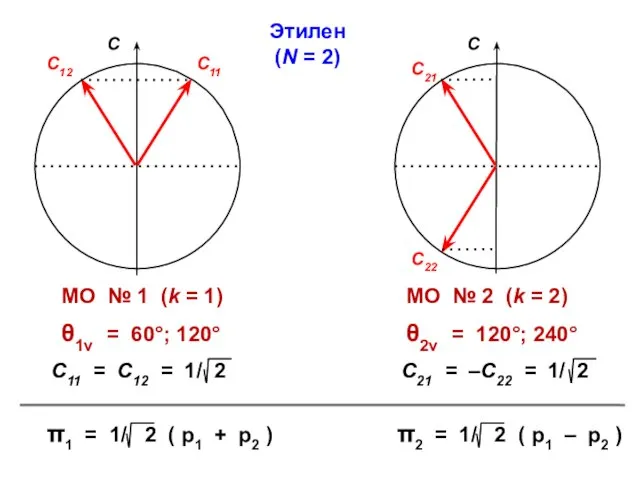
- 21. ЭТИЛЕН π1 = С11 p1 + C12 p2 π2 = С21 p1 + C22 p2 Энергии
- 22. С1 ⋅ Х + С2 = 0 С1 + С2 ⋅ Х = 0
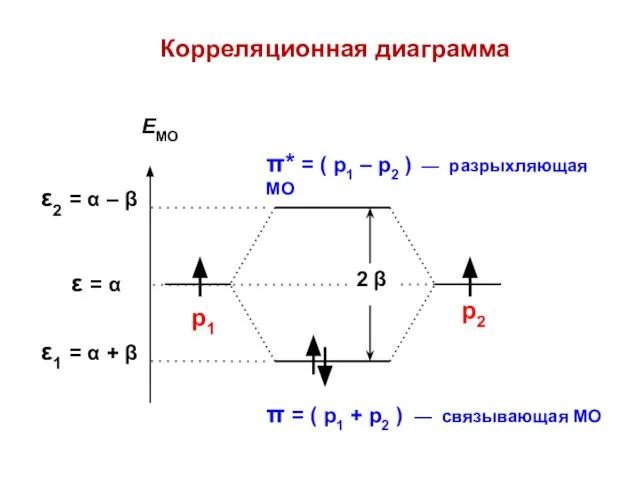
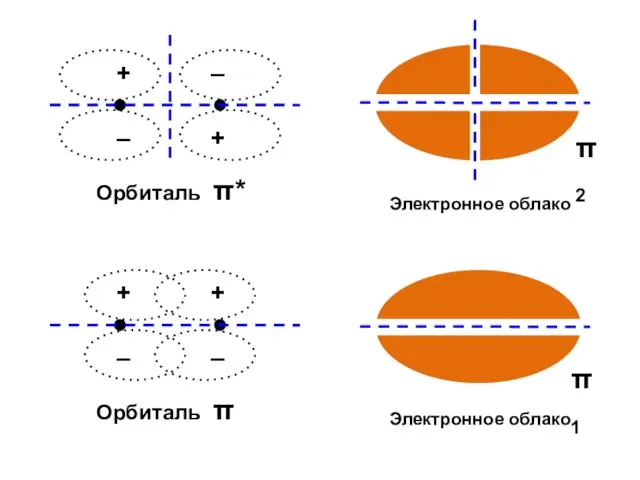
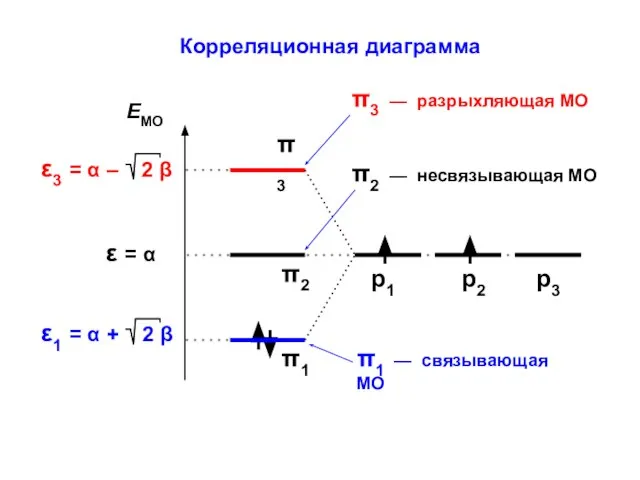
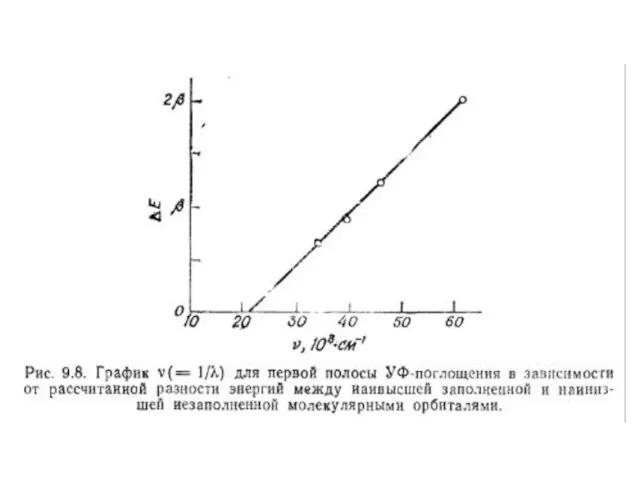
- 23. ε1 = α – β ε2 = α + β МО АО Атомно-молекулярная матрица
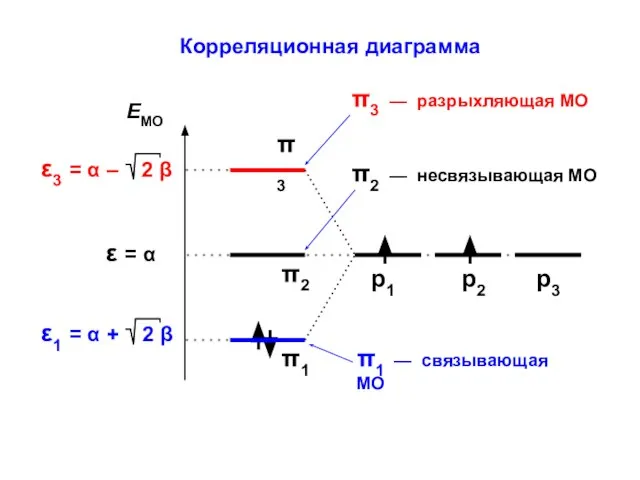
- 24. Корреляционная диаграмма
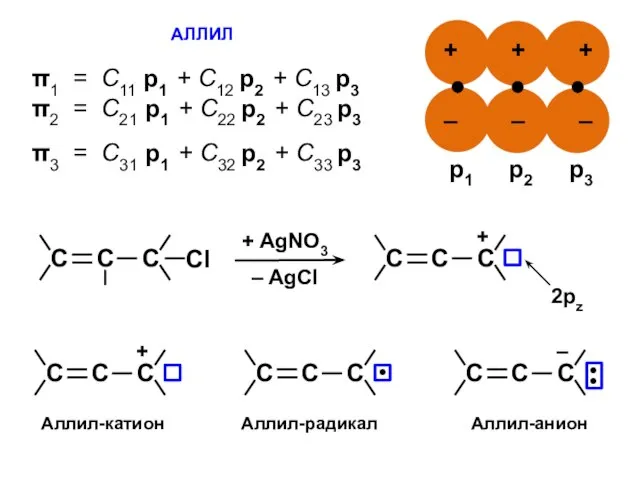
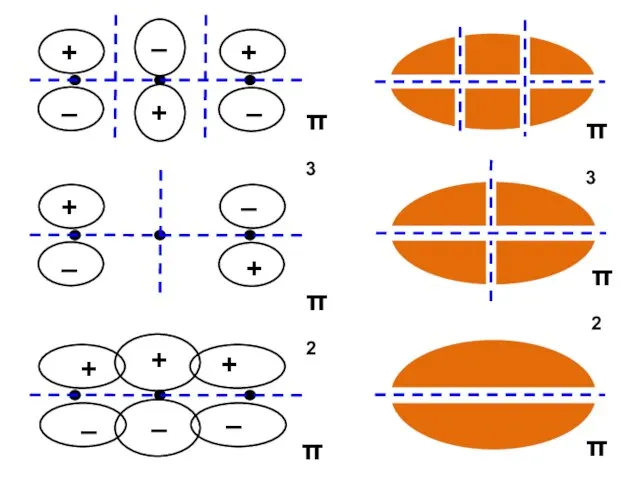
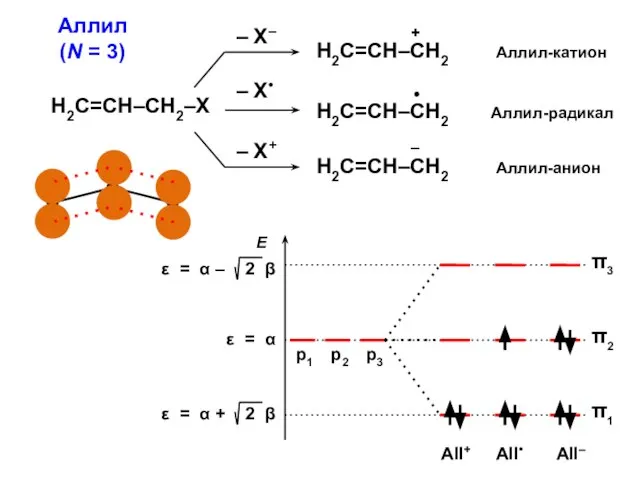
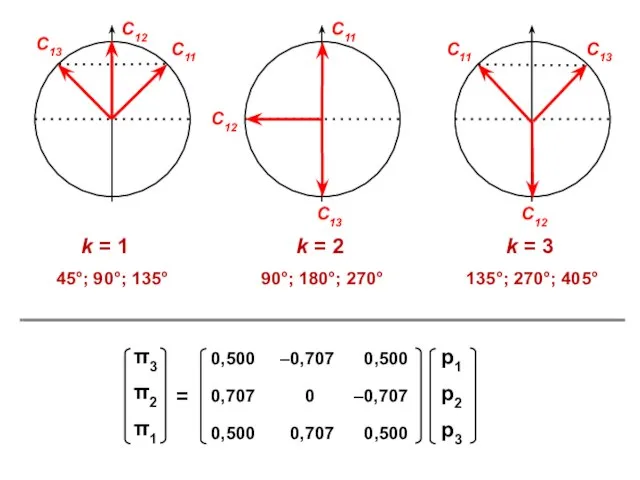
- 26. АЛЛИЛ π1 = С11 p1 + C12 p2 + C13 p3 π2 = С21 p1 +
- 28. С1 ⋅ Х + С2 + 0 = 0 С1 + С2 ⋅ Х + С3
- 30. Корреляционная диаграмма
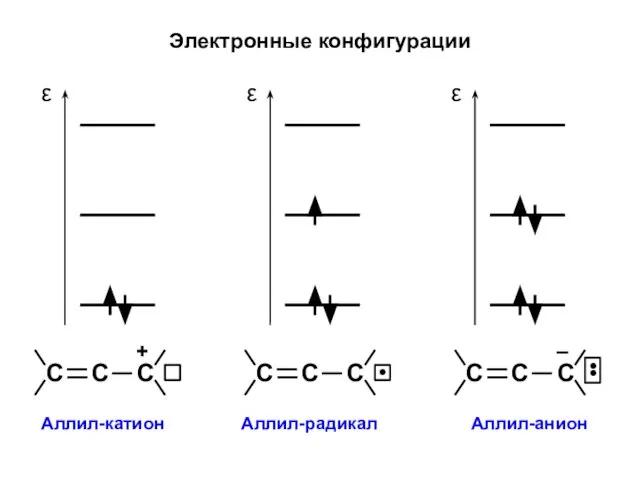
- 31. Электронные конфигурации
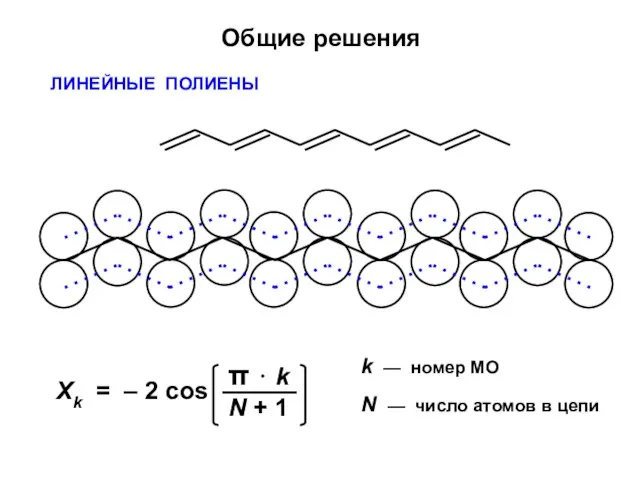
- 34. Общие решения ЛИНЕЙНЫЕ ПОЛИЕНЫ k — номер МО N — число атомов в цепи
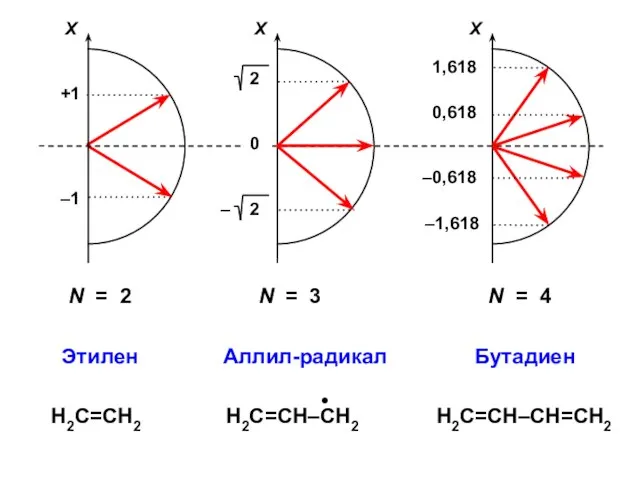
- 35. N = 2 N = 3 N = 4
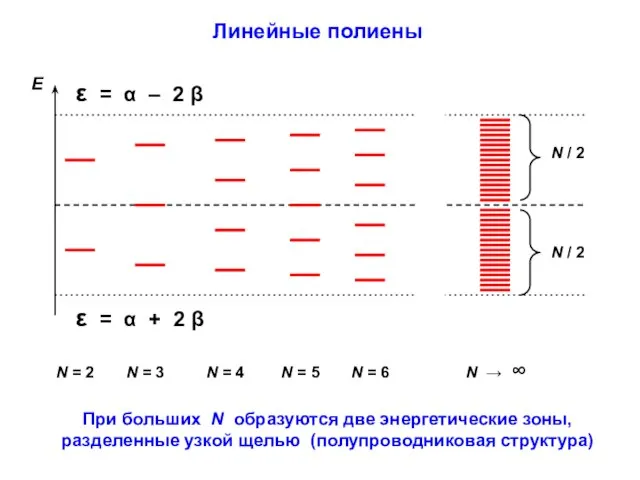
- 36. При больших N образуются две энергетические зоны, разделенные узкой щелью (полупроводниковая структура) Линейные полиены
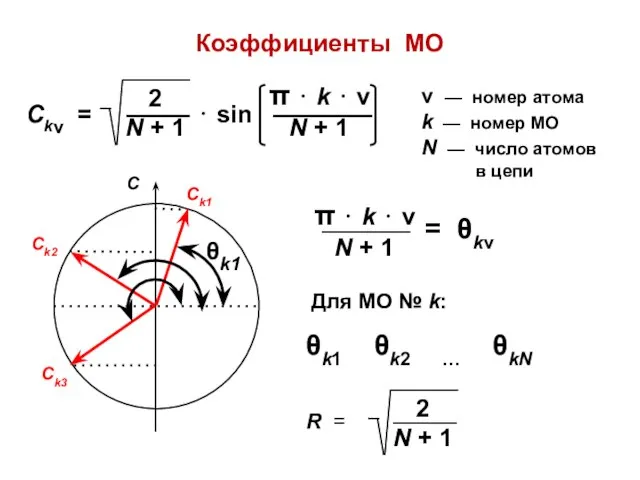
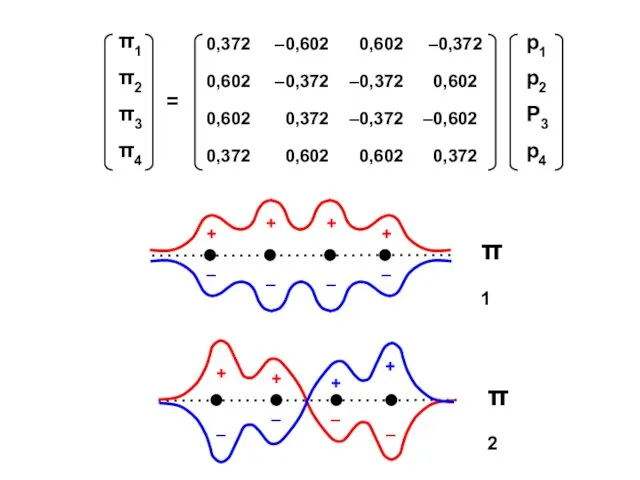
- 37. Коэффициенты МО
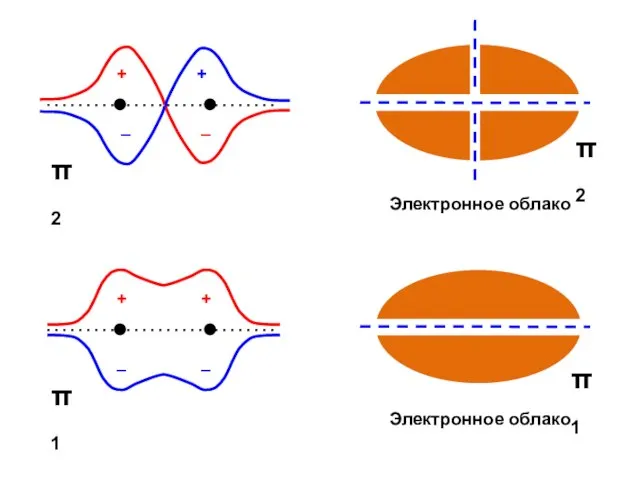
- 38. Этилен N = 2
- 39. Этилен (N = 2)
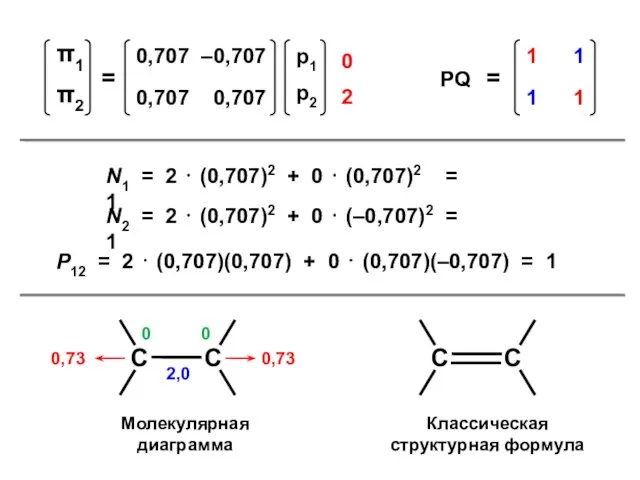
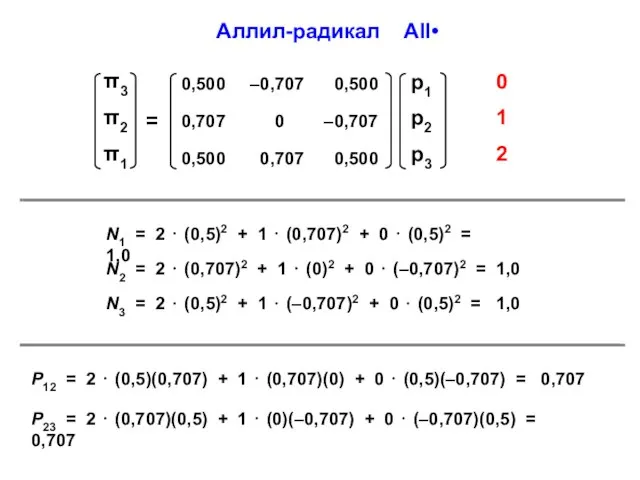
- 41. N1 = 2 ⋅ (0,707)2 + 0 ⋅ (0,707)2 = 1 N2 = 2 ⋅ (0,707)2
- 42. Аллил (N = 3) Н2С=СН–СН2–Х
- 45. Корреляционная диаграмма
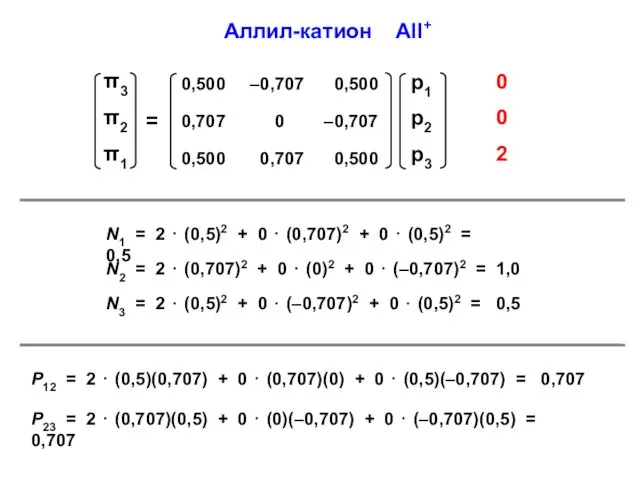
- 46. Аллил-катион All+ N1 = 2 ⋅ (0,5)2 + 0 ⋅ (0,707)2 + 0 ⋅ (0,5)2 =
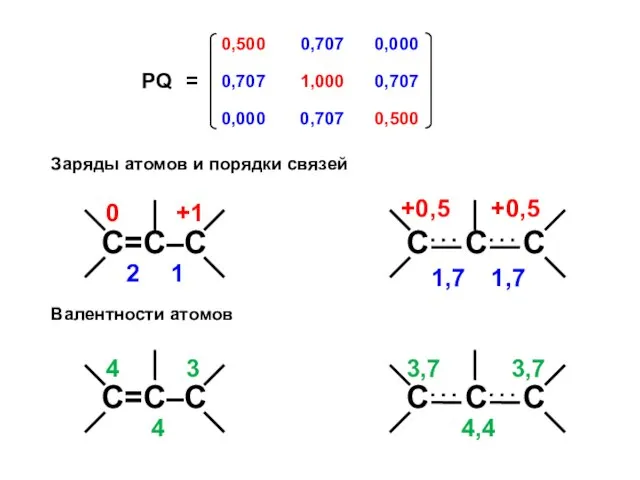
- 47. Заряды атомов и порядки связей Валентности атомов
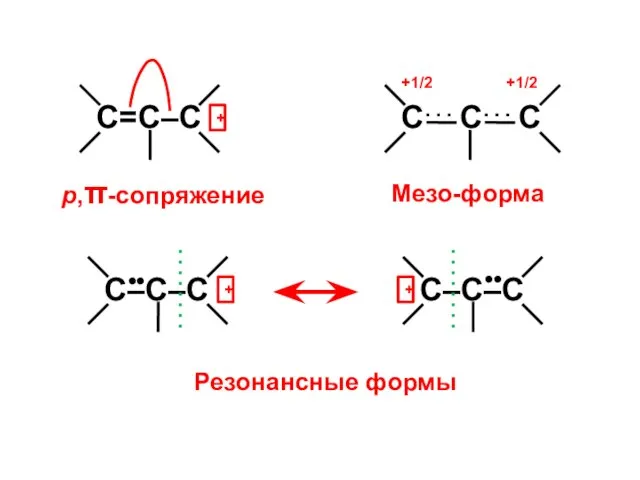
- 48. р,π-сопряжение Мезо-форма +1/2 +1/2
- 49. Аллил-радикал All• N1 = 2 ⋅ (0,5)2 + 1 ⋅ (0,707)2 + 0 ⋅ (0,5)2 =
- 50. Заряды атомов и порядки связей Валентности атомов
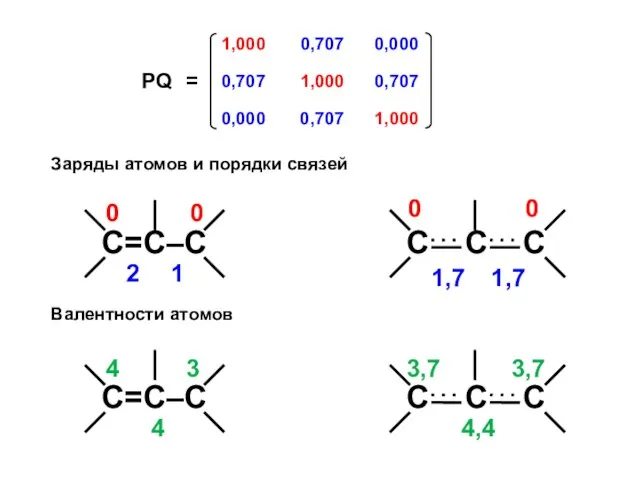
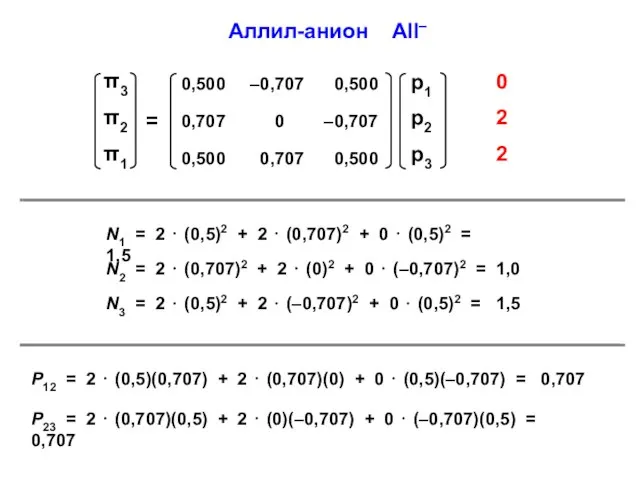
- 51. Аллил-анион All– N1 = 2 ⋅ (0,5)2 + 2 ⋅ (0,707)2 + 0 ⋅ (0,5)2 =
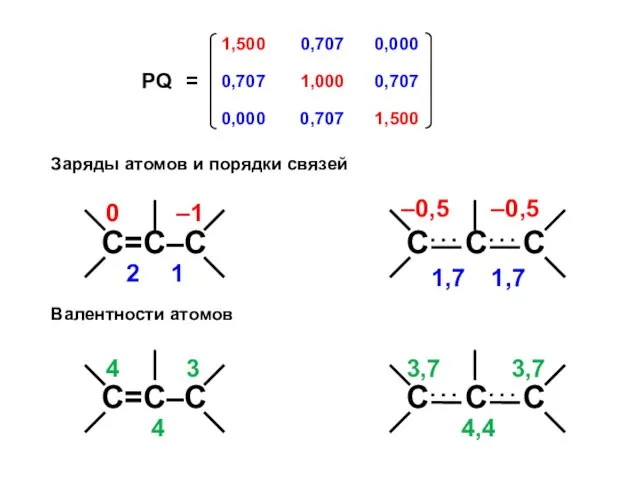
- 52. Заряды атомов и порядки связей Валентности атомов
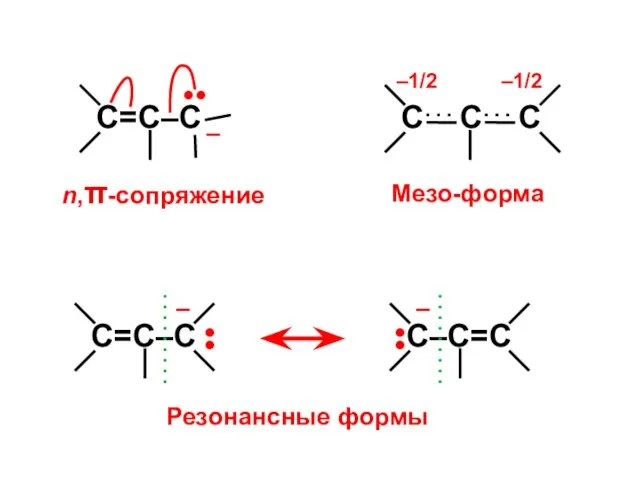
- 53. n,π-сопряжение Мезо-форма •• – –1/2 –1/2
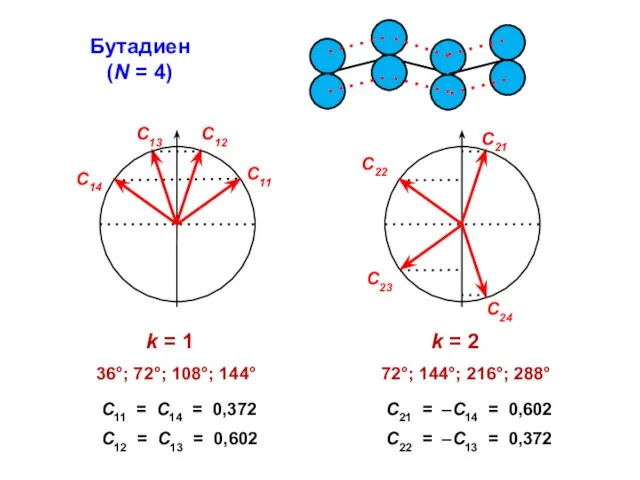
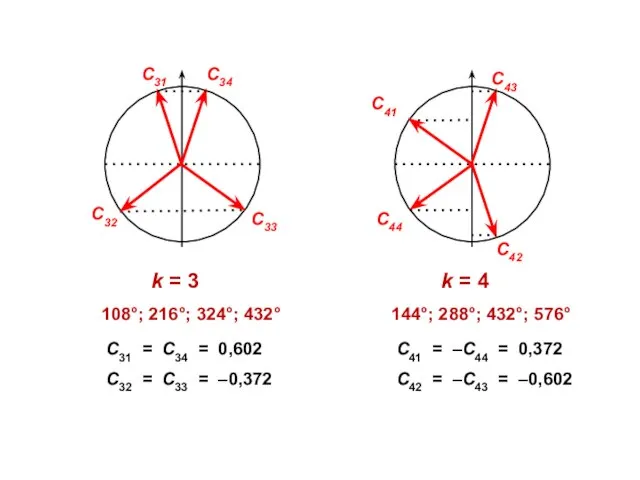
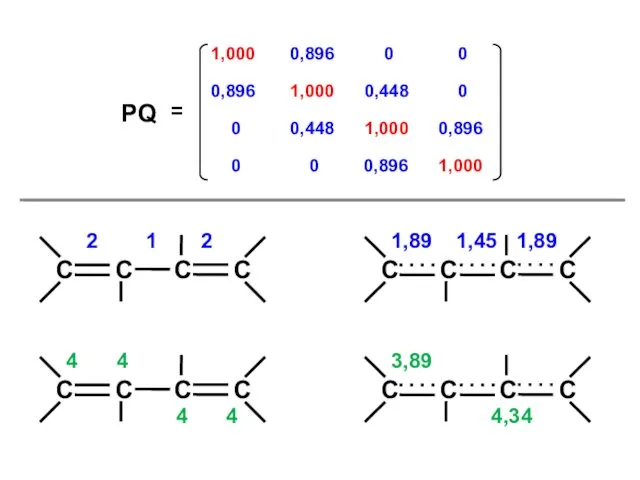
- 54. Бутадиен (N = 4)
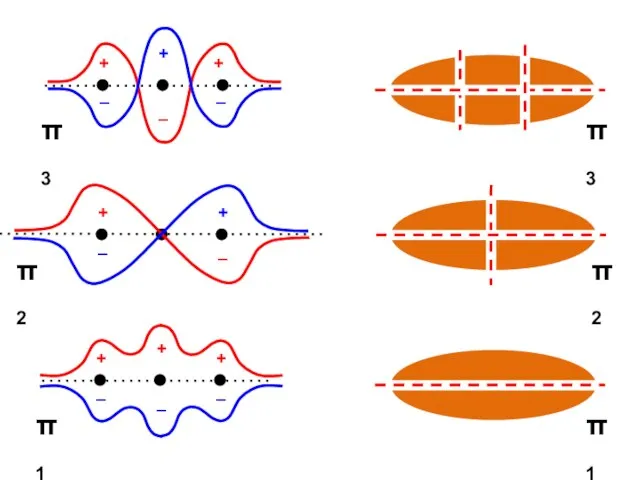
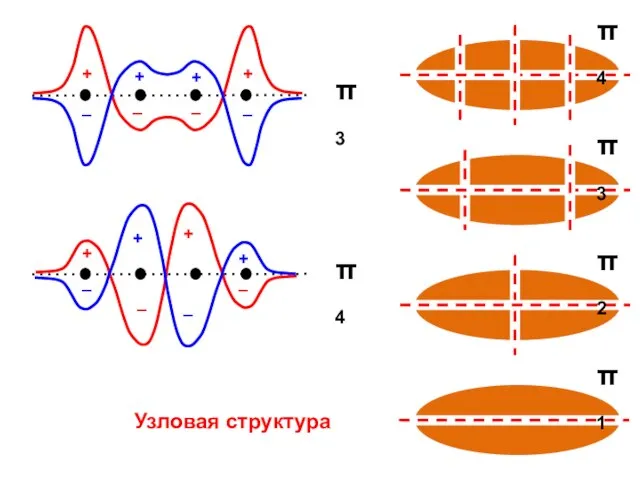
- 57. Узловая структура
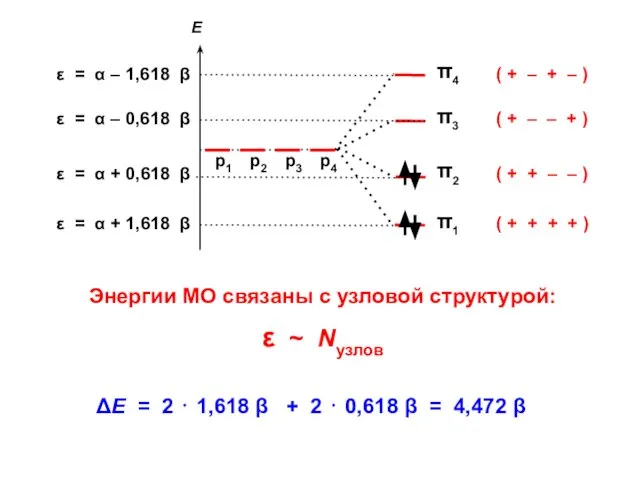
- 58. ( + + + + ) ( + + – – ) ( + – –
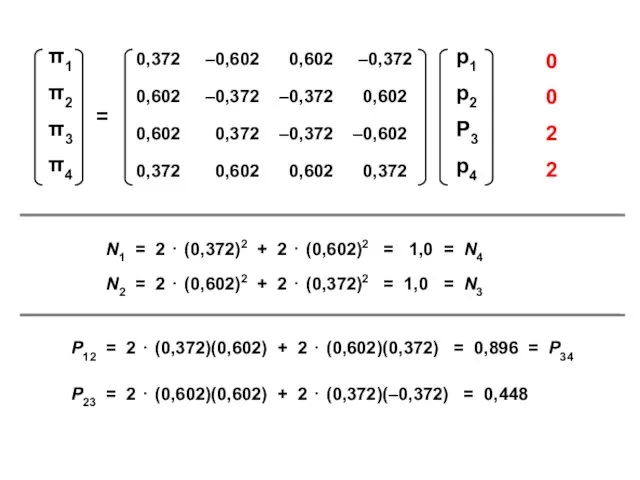
- 59. N1 = 2 ⋅ (0,372)2 + 2 ⋅ (0,602)2 = 1,0 = N4 N2 = 2
- 60. 4 4 4 4 3,89 4,34 2 2 1 1,89 1,89 1,45
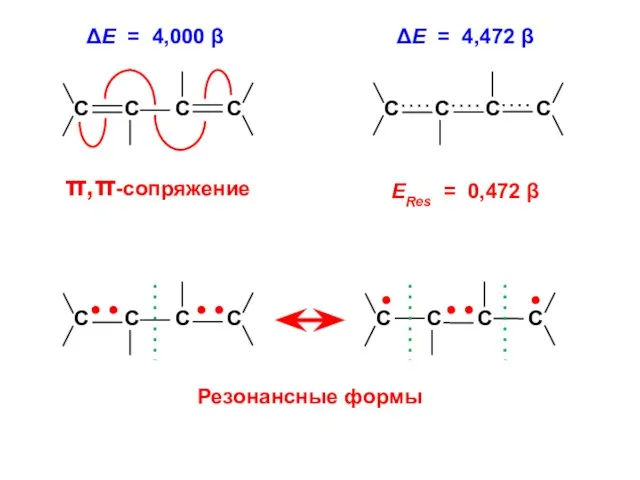
- 61. . С С С С ΔЕ = 4,472 β ΔЕ = 4,000 β ЕRes = 0,472
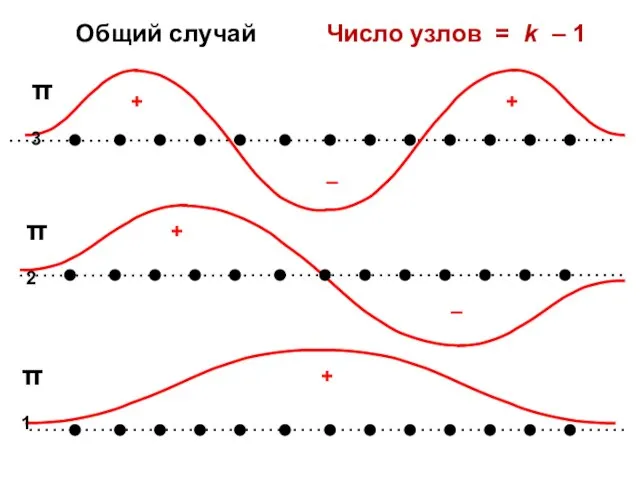
- 62. Общий случай Число узлов = k – 1
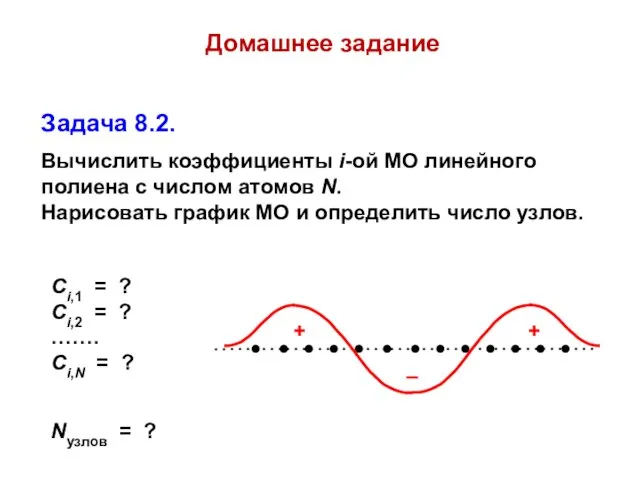
- 63. Домашнее задание Задача 8.2. Вычислить коэффициенты i-ой МО линейного полиена с числом атомов N. Нарисовать график
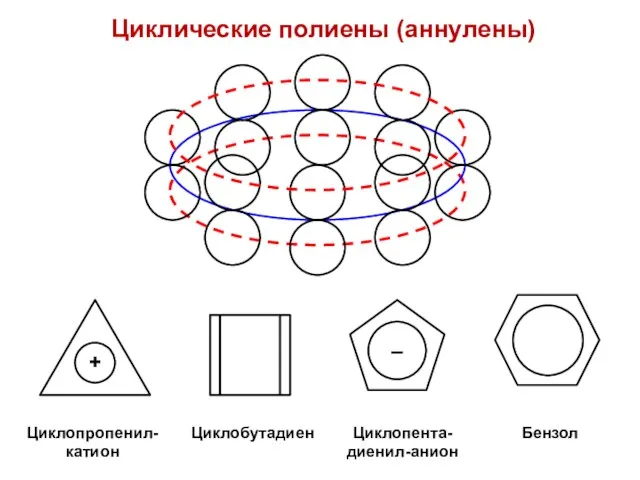
- 64. Циклические полиены (аннулены)
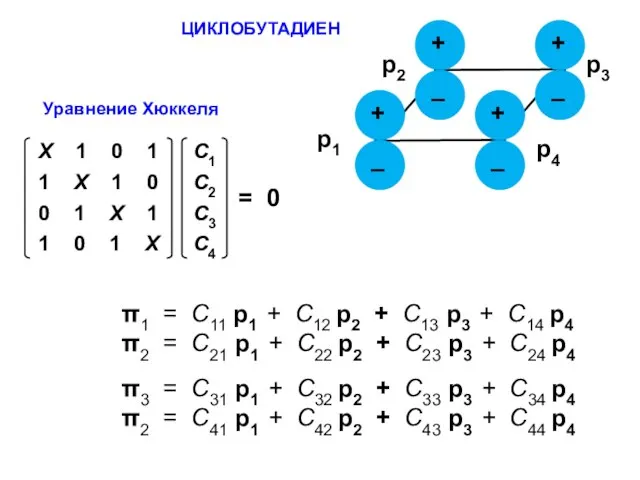
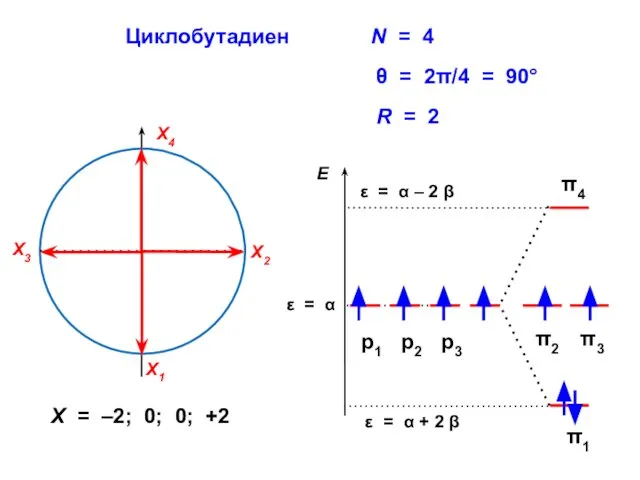
- 65. ЦИКЛОБУТАДИЕН π1 = С11 p1 + C12 p2 + С13 p3 + C14 p4 π2 =
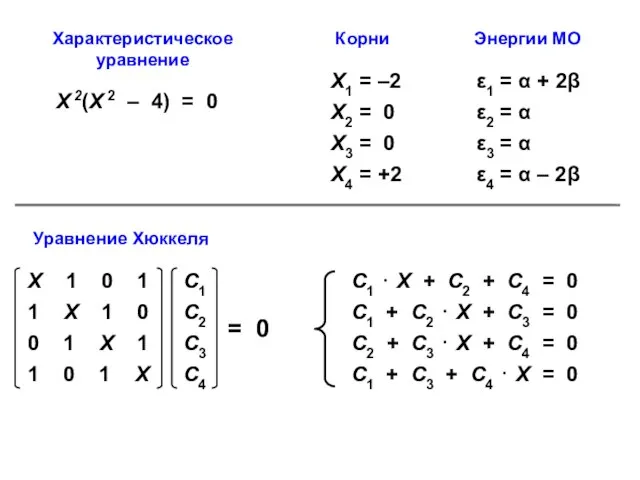
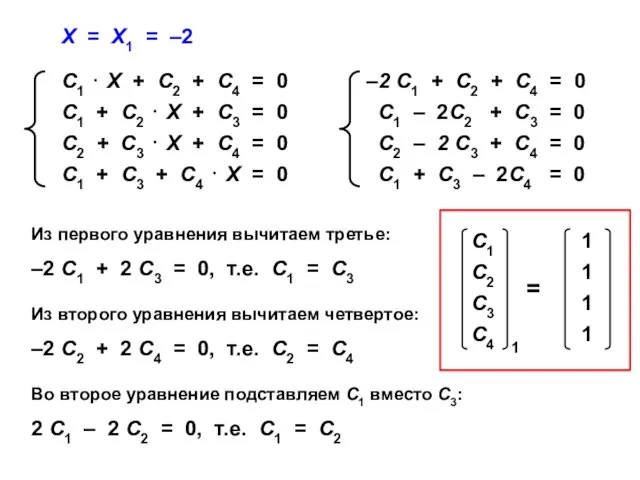
- 67. Х = Х1 = –2 Из первого уравнения вычитаем третье: –2 С1 + 2 С3 =
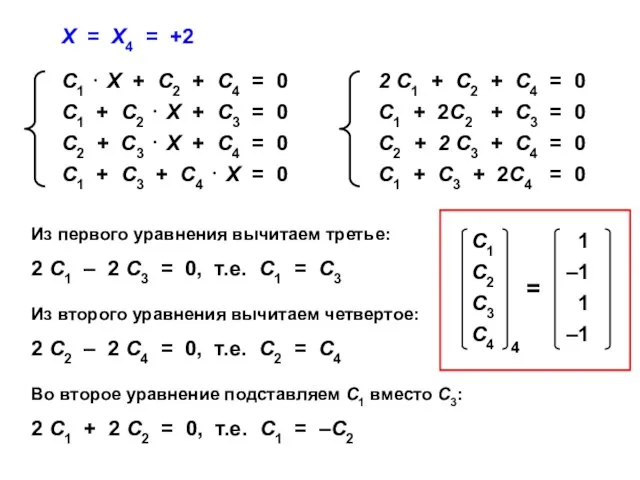
- 68. Х = Х4 = +2 Из первого уравнения вычитаем третье: 2 С1 – 2 С3 =
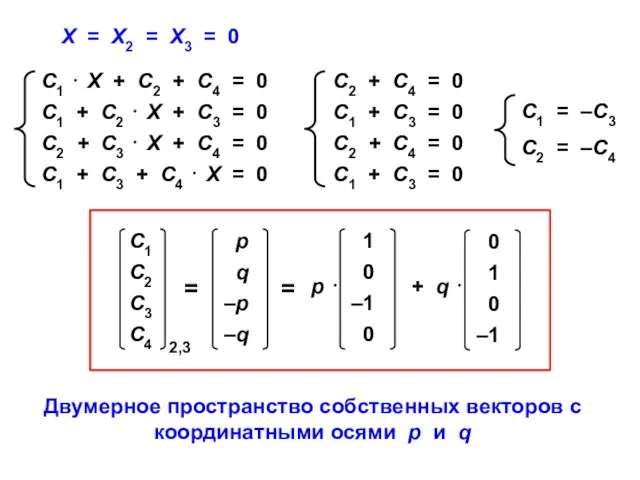
- 69. Х = Х2 = Х3 = 0 Двумерное пространство собственных векторов с координатными осями p и
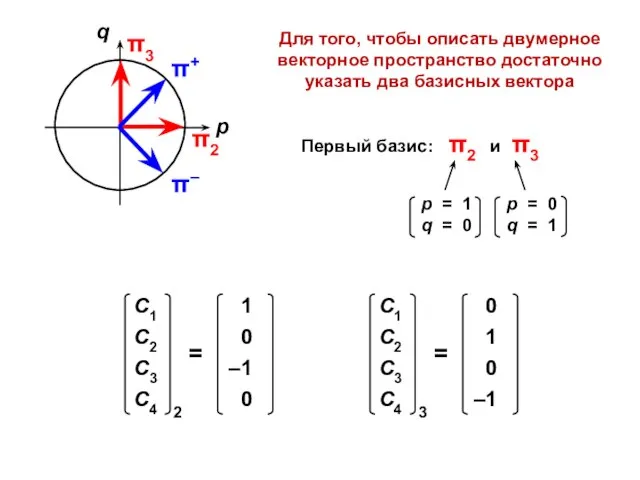
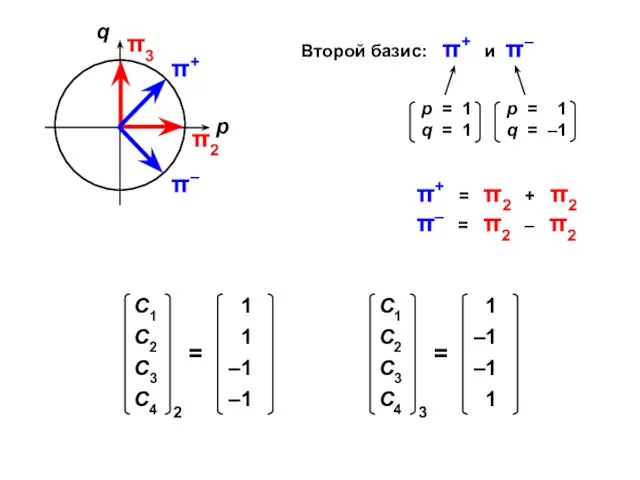
- 70. Для того, чтобы описать двумерное векторное пространство достаточно указать два базисных вектора Первый базис: π2 и
- 71. Второй базис: π+ и π– π+ = π2 + π2 π– = π2 – π2
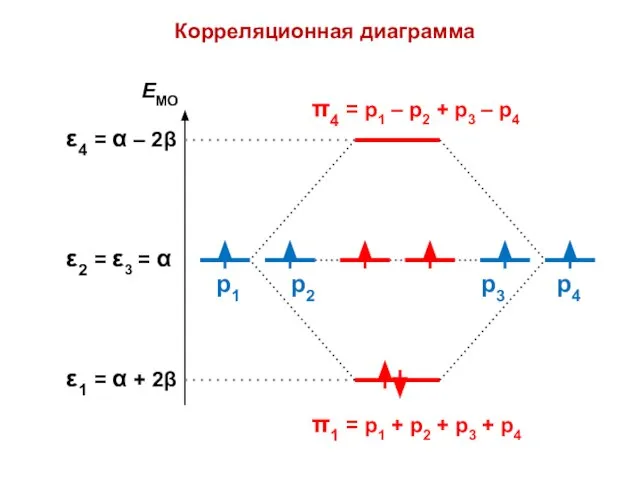
- 72. Корреляционная диаграмма
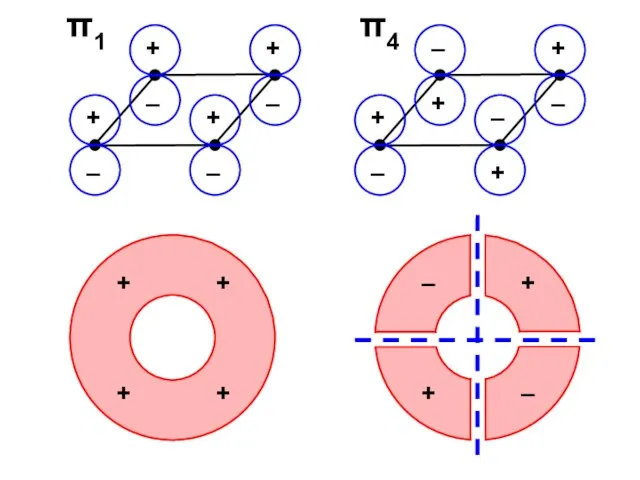
- 73. π1 π4
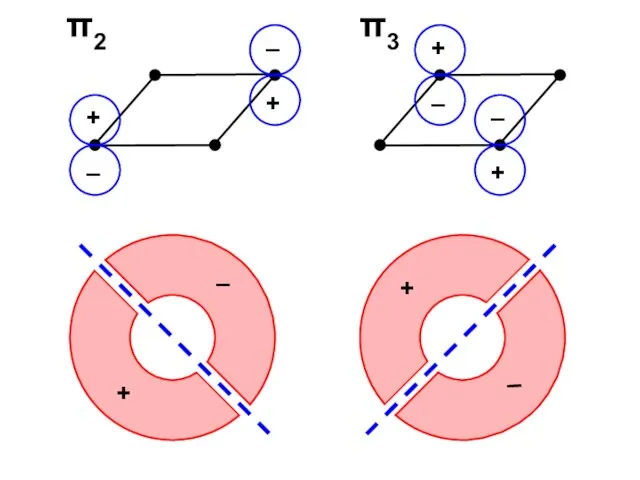
- 74. π2 π3
- 75. π+ π–
- 76. k — номер МО N — число атомов в цикле Орбитальные энергии θ = 2π/N R
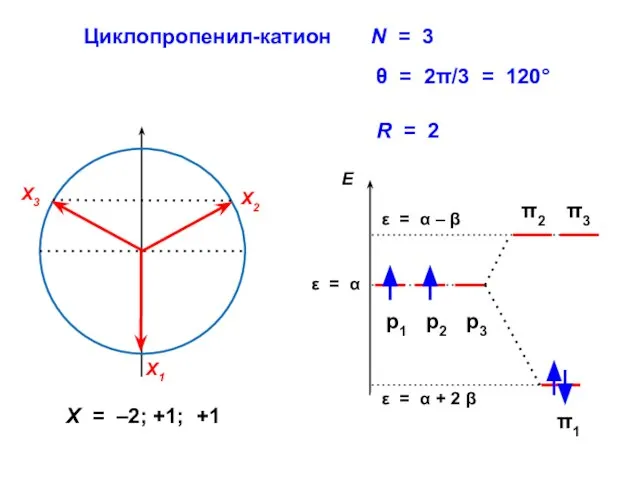
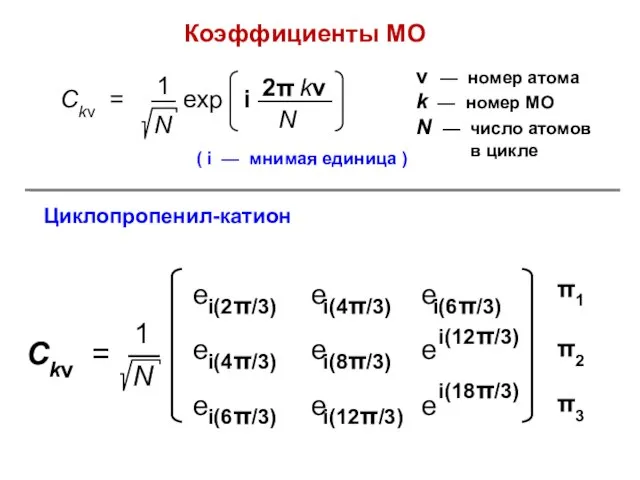
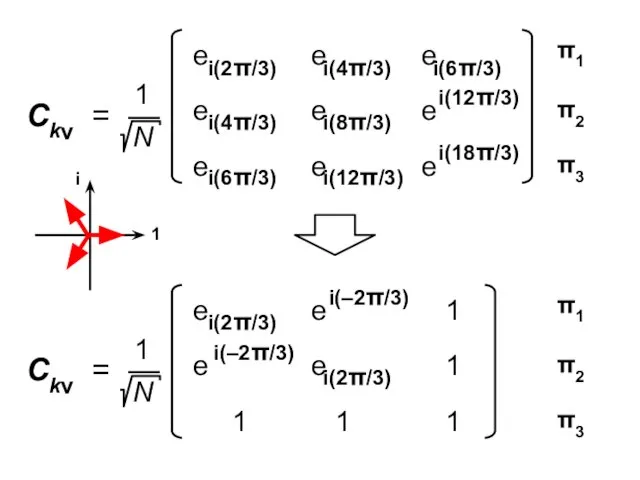
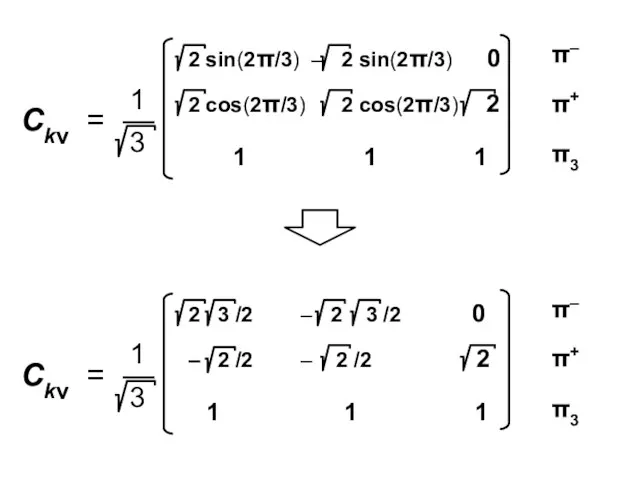
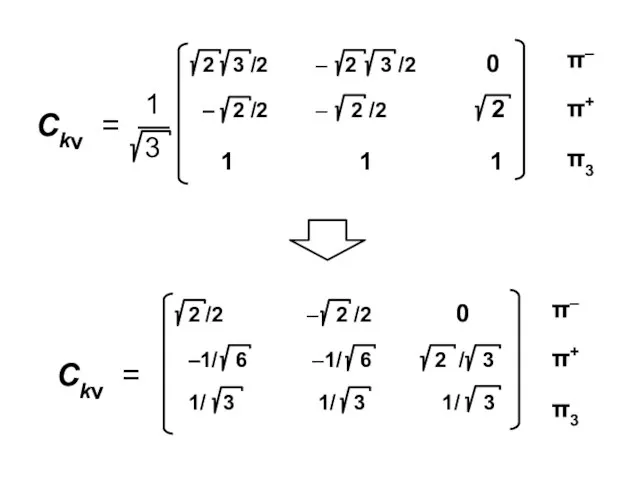
- 77. Циклопропенил-катион R = 2 X = –2; +1; +1
- 78. Циклобутадиен R = 2 X = –2; 0; 0; +2
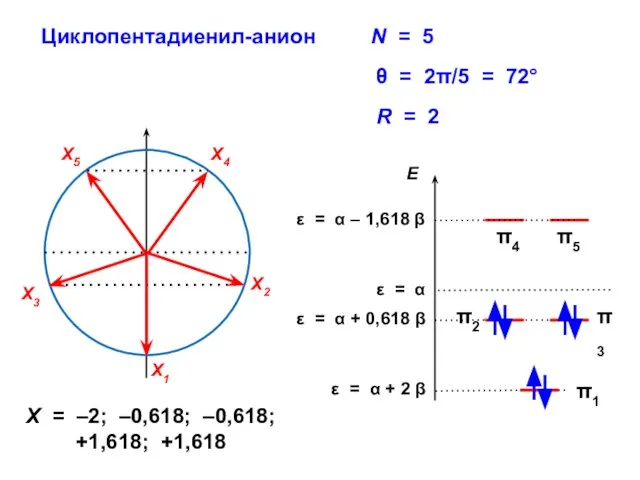
- 79. Циклопентадиенил-анион R = 2 X = –2; –0,618; –0,618; +1,618; +1,618
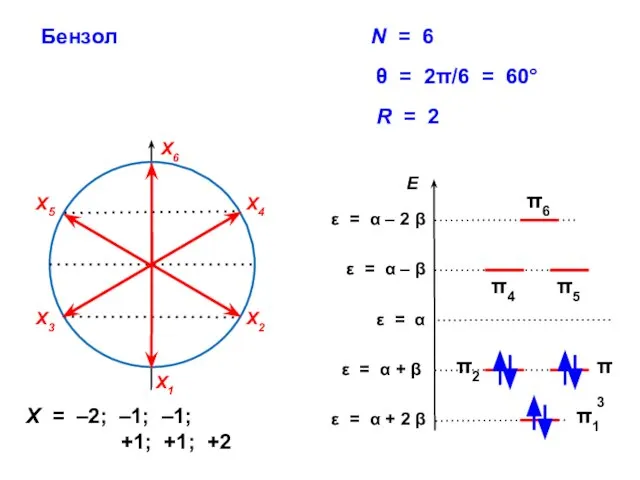
- 80. Бензол R = 2 X = –2; –1; –1; +1; +1; +2
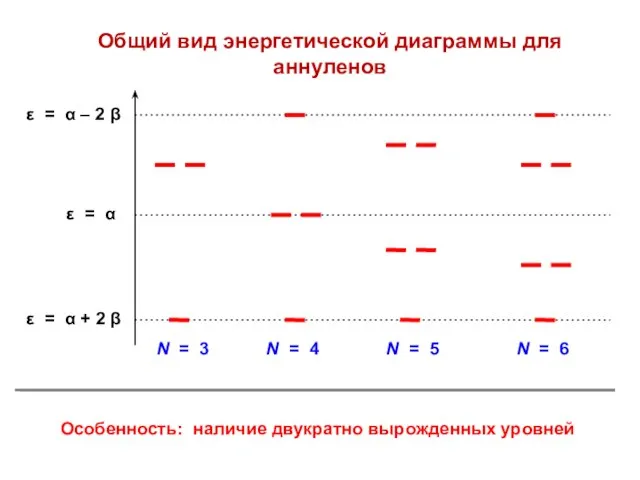
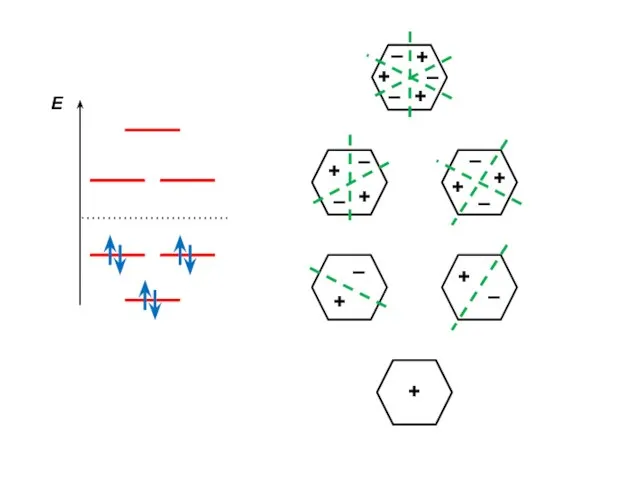
- 81. Общий вид энергетической диаграммы для аннуленов Особенность: наличие двукратно вырожденных уровней
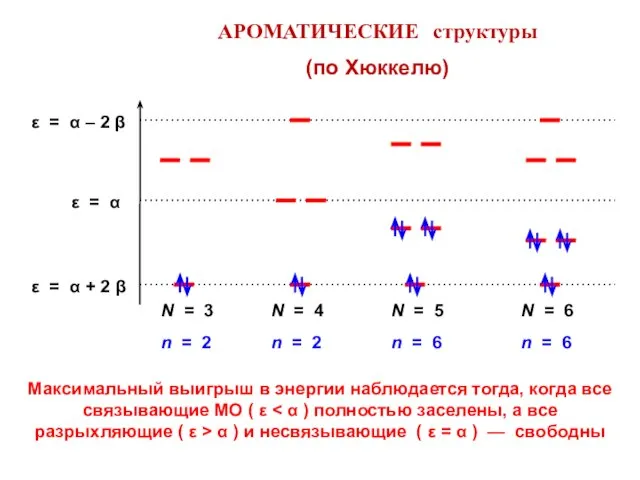
- 82. АРОМАТИЧЕСКИЕ структуры (по Хюккелю) Максимальный выигрыш в энергии наблюдается тогда, когда все связывающие МО ( ε
- 83. Число связывающих МО всегда нечетно и его можно выразить формулой (2k + 1), где k =
- 84. Циклопропенил-катион Циклопентадиенил-анион
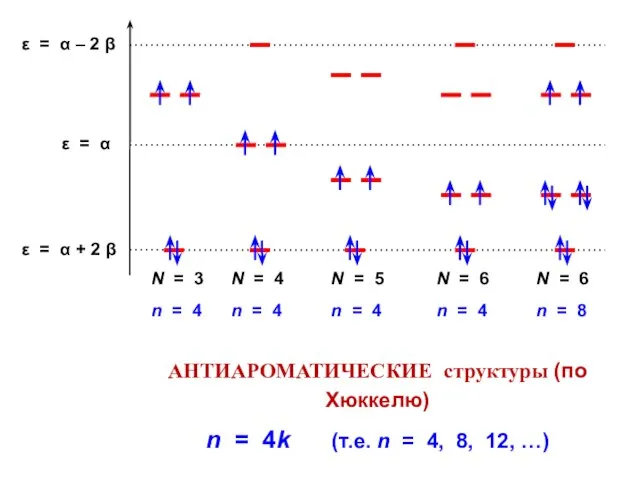
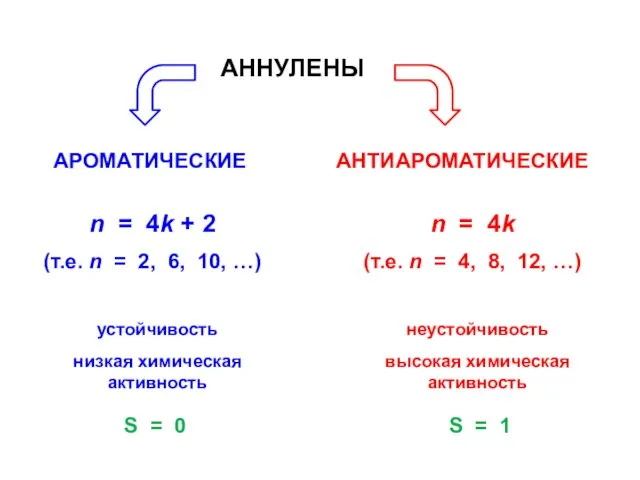
- 85. АНТИАРОМАТИЧЕСКИЕ структуры (по Хюккелю) n = 4k (т.е. n = 4, 8, 12, …)
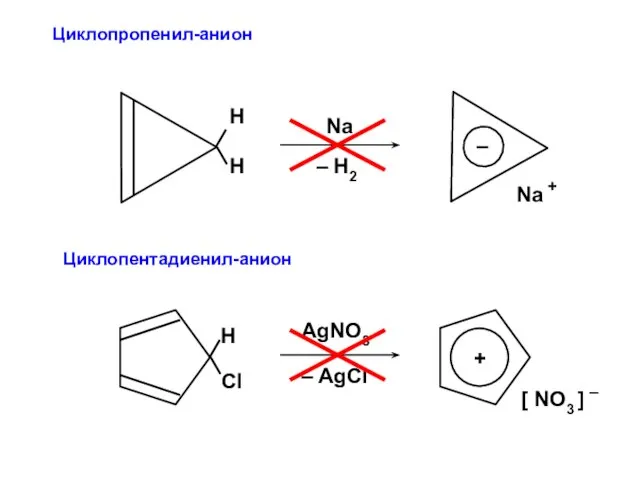
- 86. Циклопропенил-анион Циклопентадиенил-анион
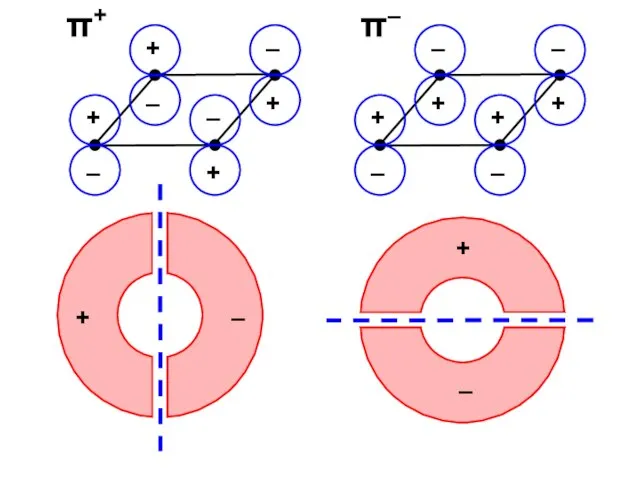
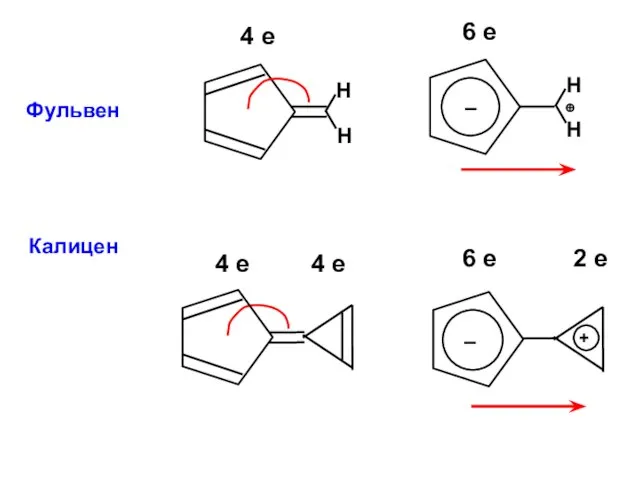
- 87. Фульвен 4 е
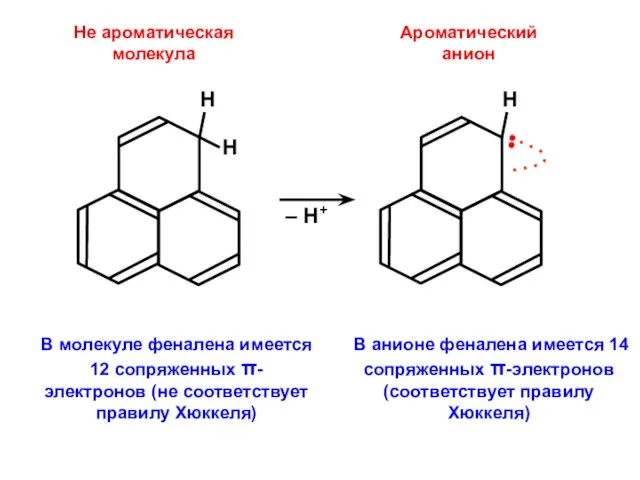
- 88. Не ароматическая молекула В анионе феналена имеется 14 сопряженных π-электронов (соответствует правилу Хюккеля) В молекуле феналена
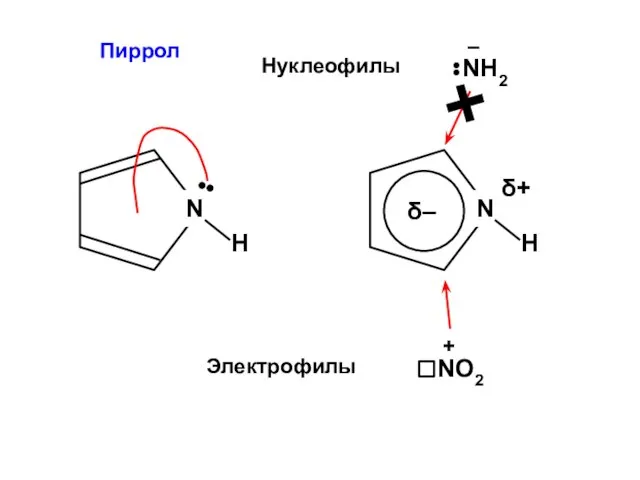
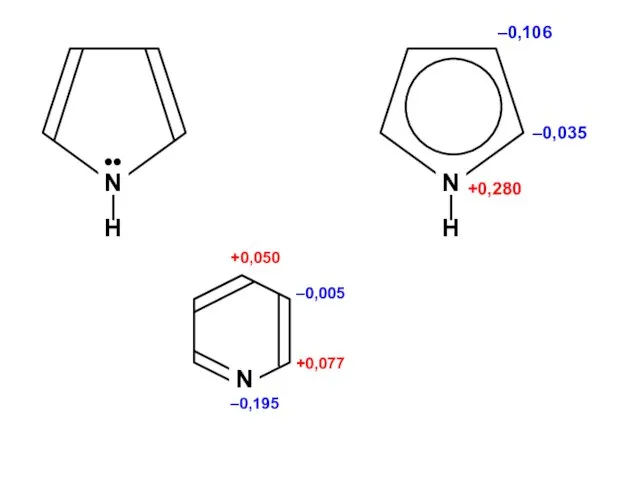
- 89. Пиррол N H ••
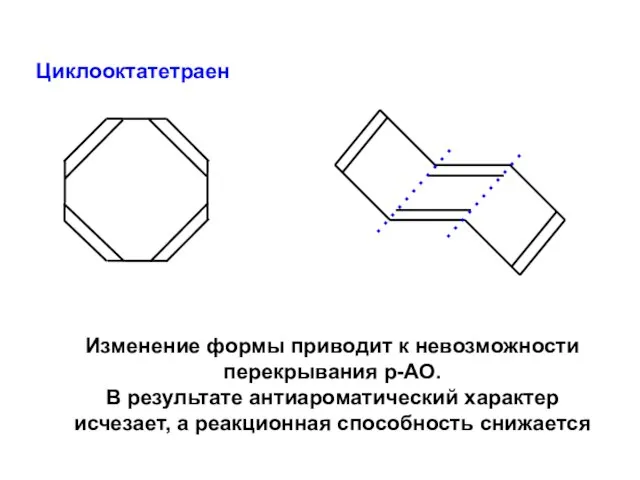
- 90. Циклооктатетраен Изменение формы приводит к невозможности перекрывания р-АО. В результате антиароматический характер исчезает, а реакционная способность
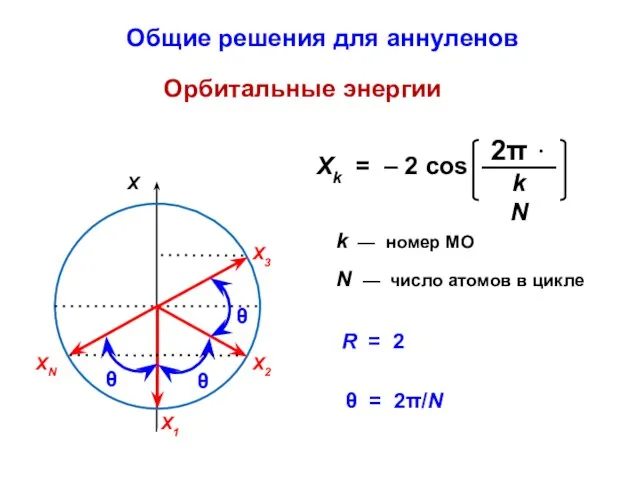
- 91. АННУЛЕНЫ n = 4k + 2 (т.е. n = 2, 6, 10, …) устойчивость низкая химическая
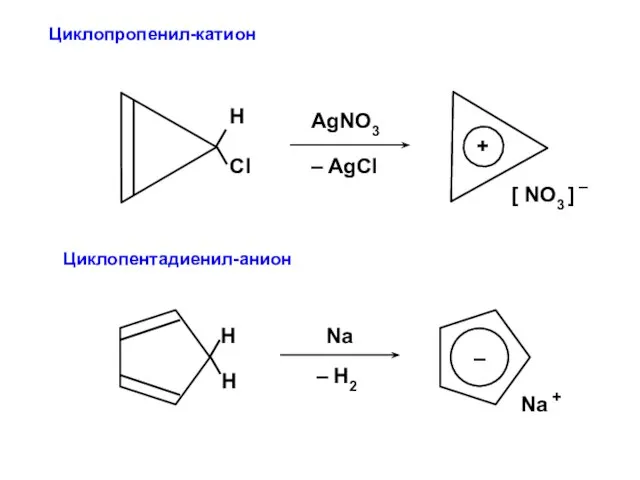
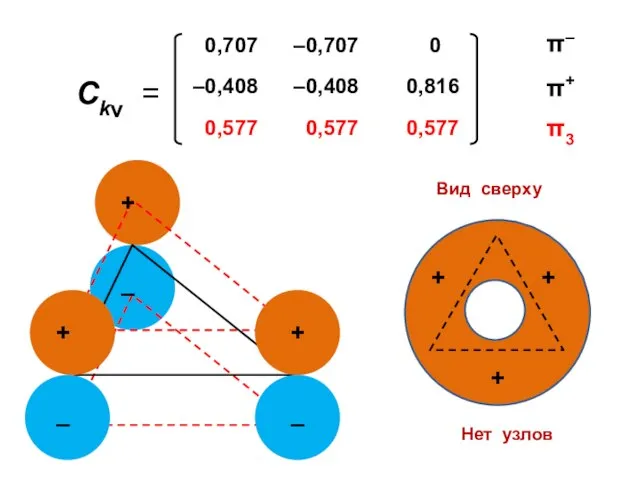
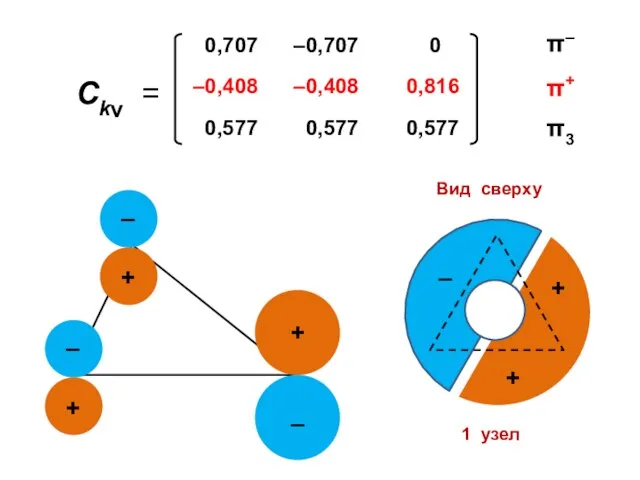
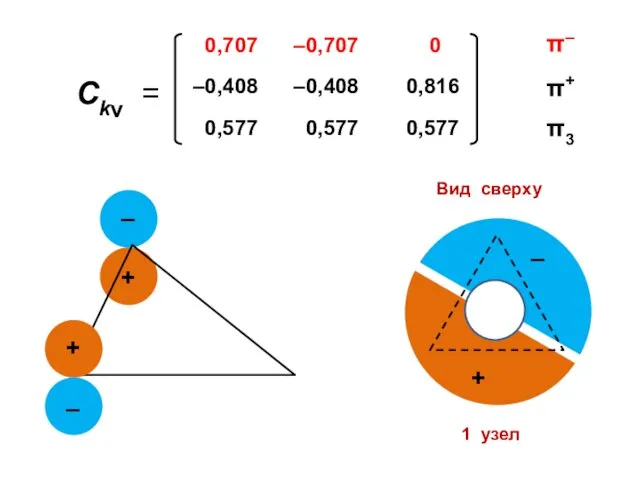
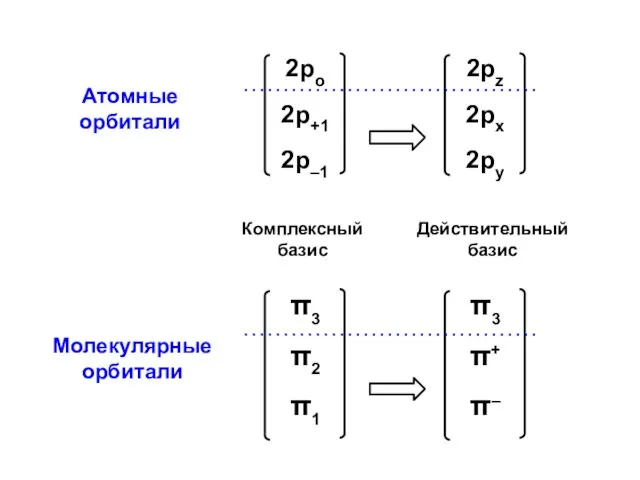
- 92. Коэффициенты МО ( i — мнимая единица ) ν — номер атома k — номер МО
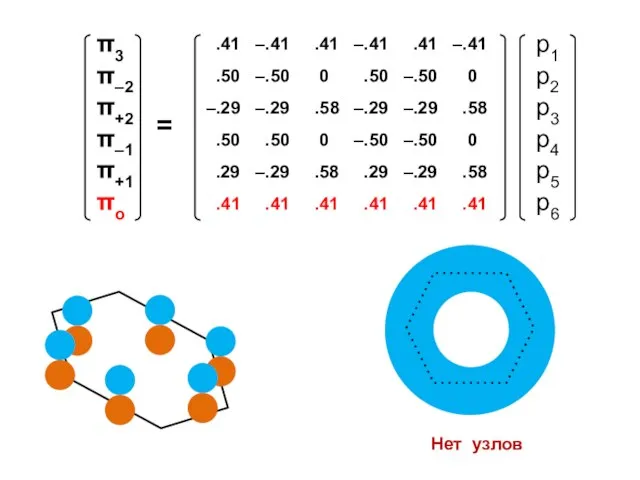
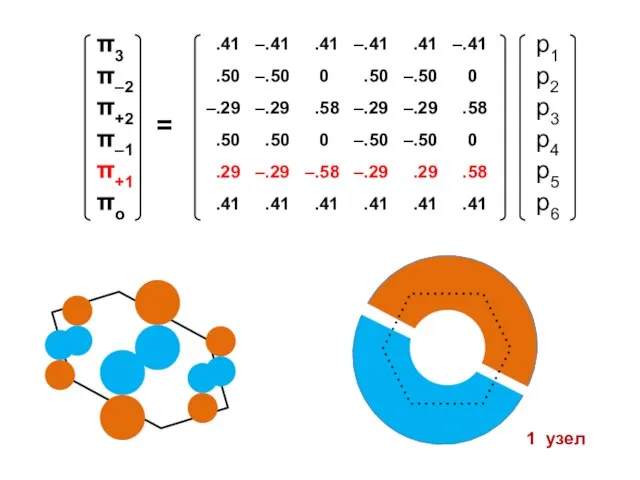
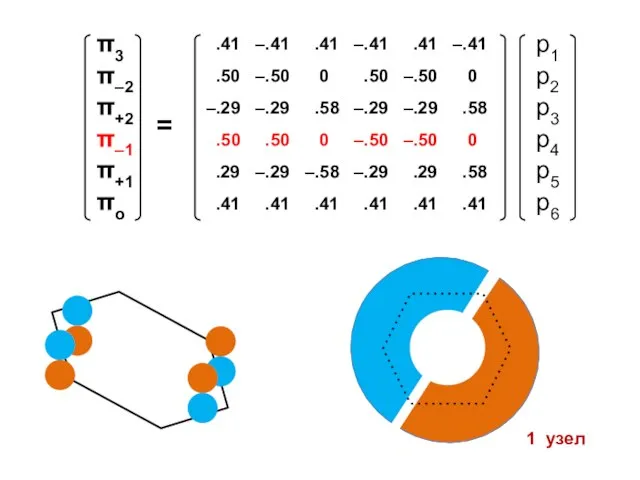
- 100. Атомные орбитали Молекулярные орбитали
- 101. Процедура преобразования к действительному базису возможна для любого аннулена
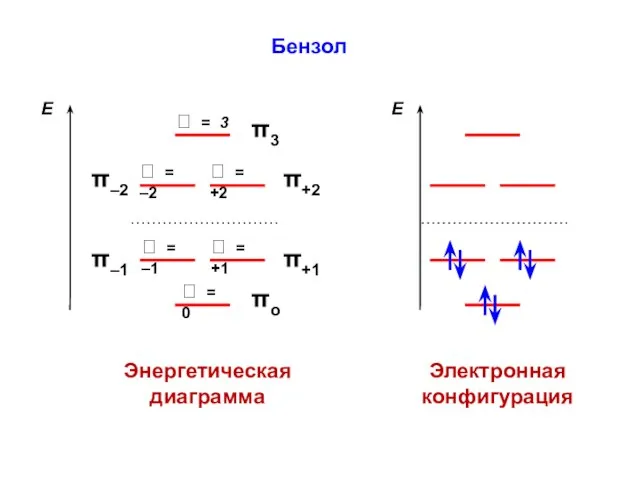
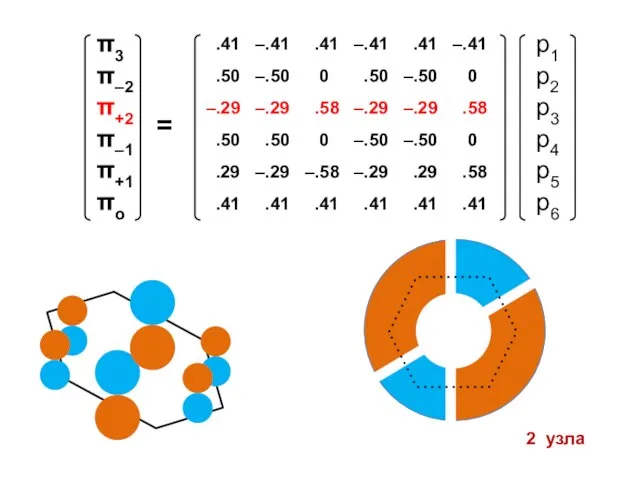
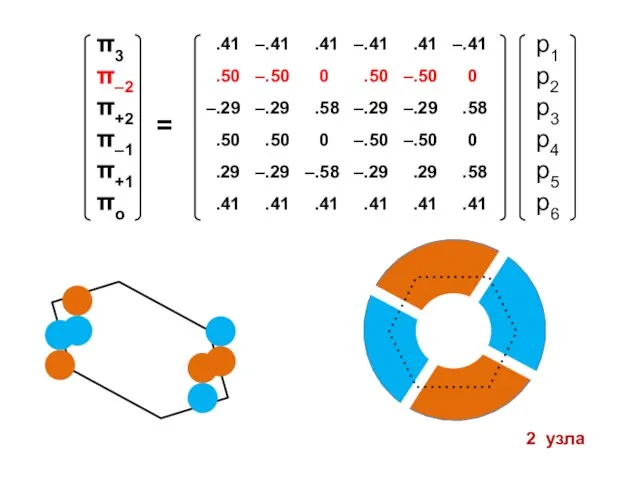
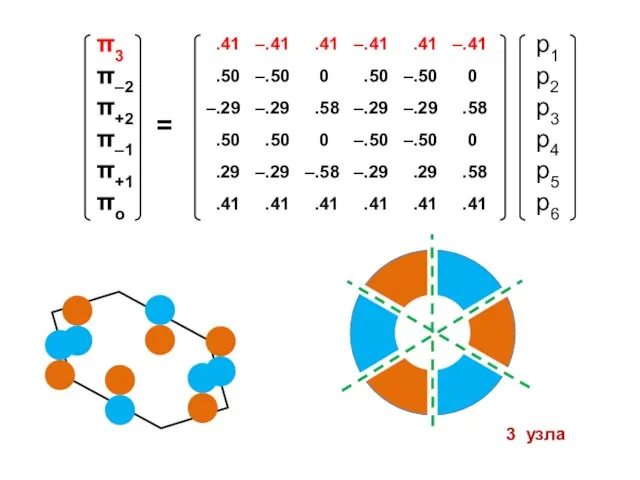
- 102. Бензол Энергетическая диаграмма Электронная конфигурация
- 105. 1 узел
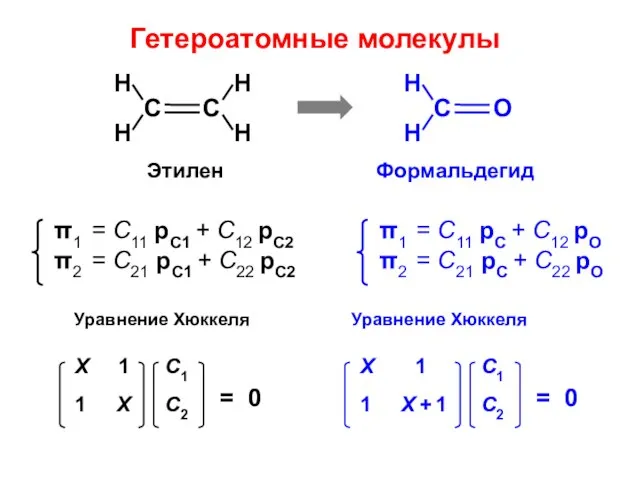
- 110. Гетероатомные молекулы
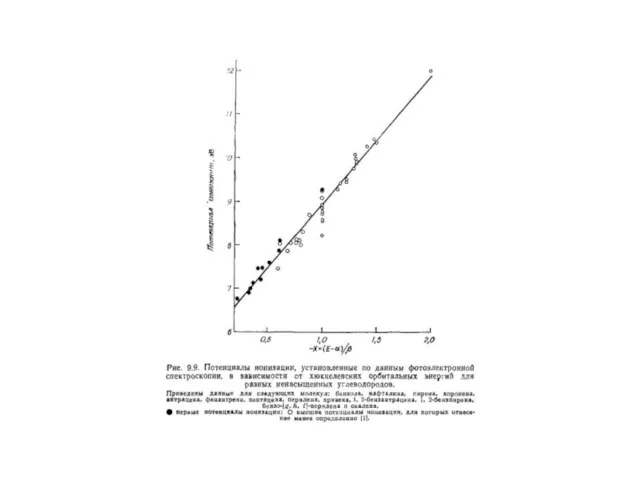
- 111. Х1 = +1 Х2 = –1 Х 2 + Х – 1 = 0 Х1 =
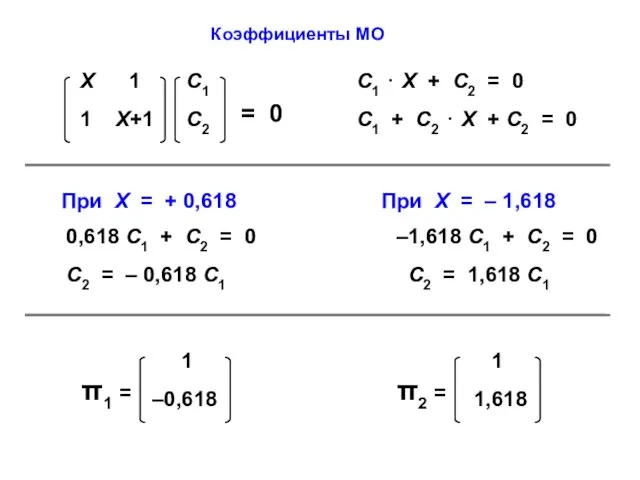
- 112. Коэффициенты МО С1 ⋅ Х + С2 = 0 С1 + С2 ⋅ Х + С2
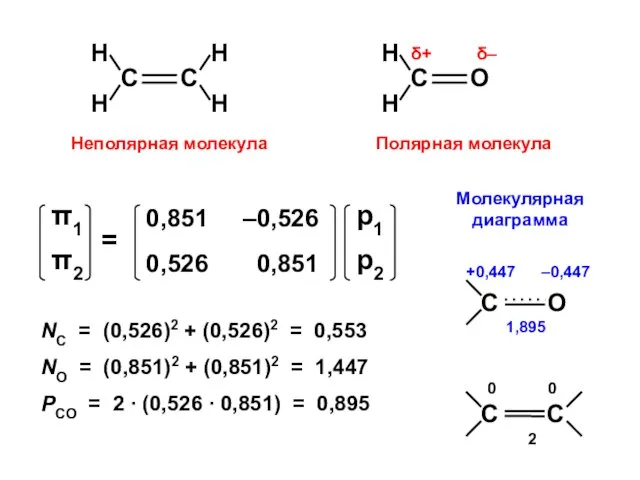
- 113. Атомно-молекулярная матрица этилен формальдегид
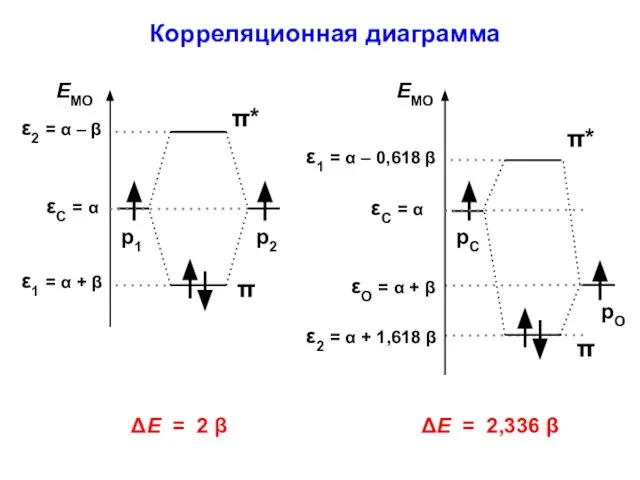
- 114. ΔЕ = 2 β Корреляционная диаграмма рО ΔЕ = 2,336 β
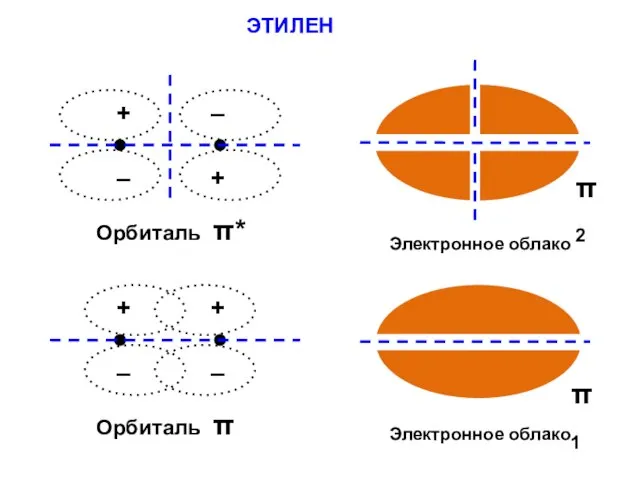
- 115. ЭТИЛЕН
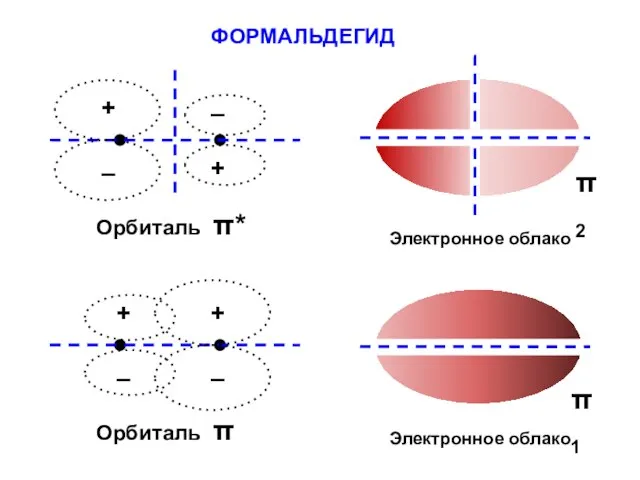
- 116. ФОРМАЛЬДЕГИД
- 117. NC = (0,526)2 + (0,526)2 = 0,553 NO = (0,851)2 + (0,851)2 = 1,447 PCO =
- 118. δ+ δ– δ– δ+
- 119. Det = Х 3 + 2Х 2 – 1,16Х – 2 = 0
- 120. nC1 = 1,035 no = 1 Q = – 0,035 nC2 = 0,983 no = 1
- 121. δ+ δ–
- 123. Корреляционная диаграмма
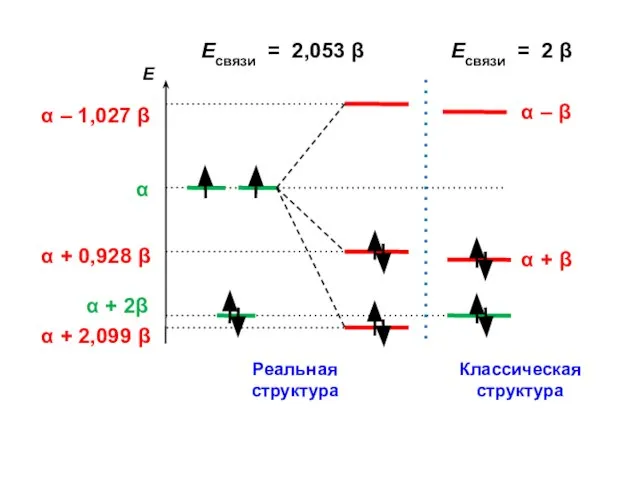
- 124. Есвязи = 2,053 β Есвязи = 2 β
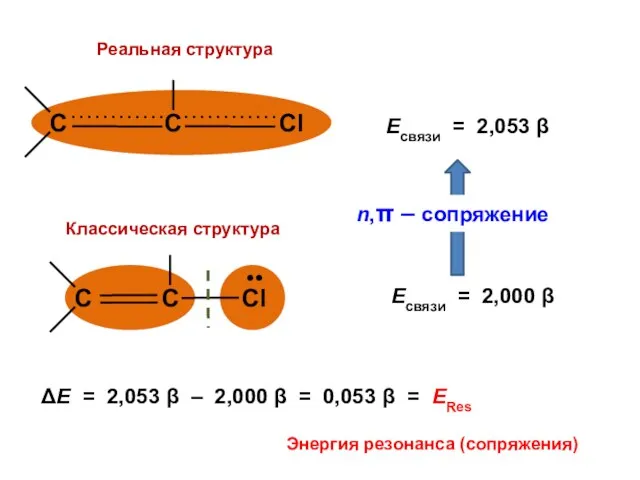
- 125. ΔЕ = 2,053 β – 2,000 β = 0,053 β = ЕRes Энергия резонанса (сопряжения)
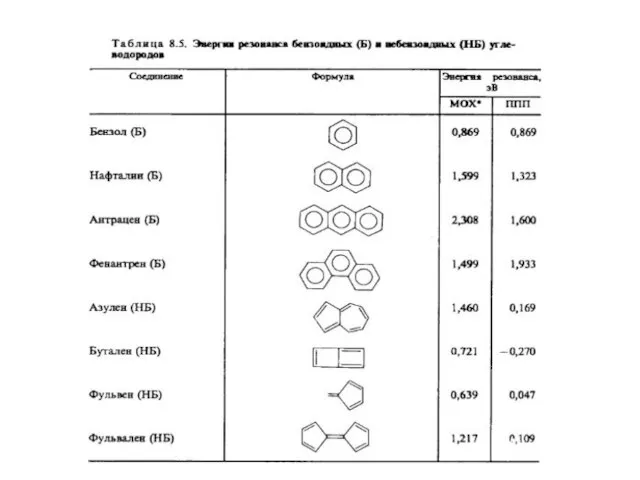
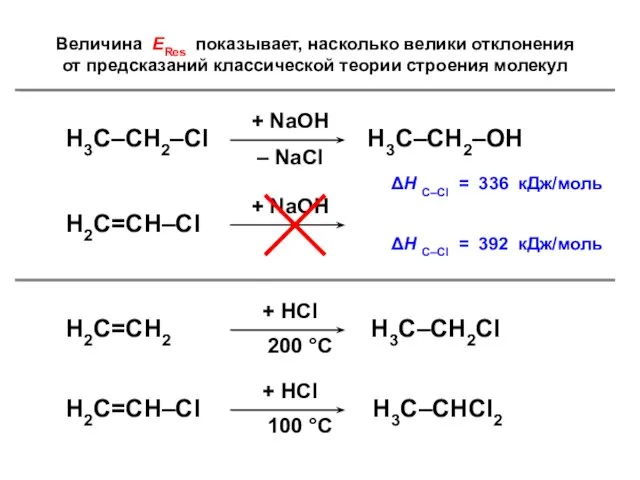
- 127. Величина ЕRes показывает, насколько велики отклонения от предсказаний классической теории строения молекул
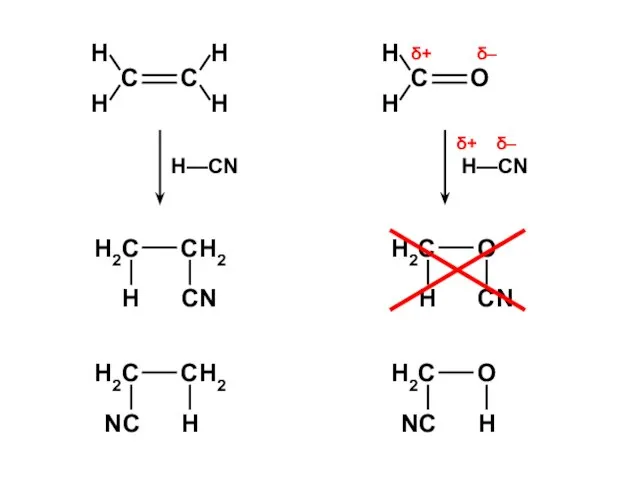
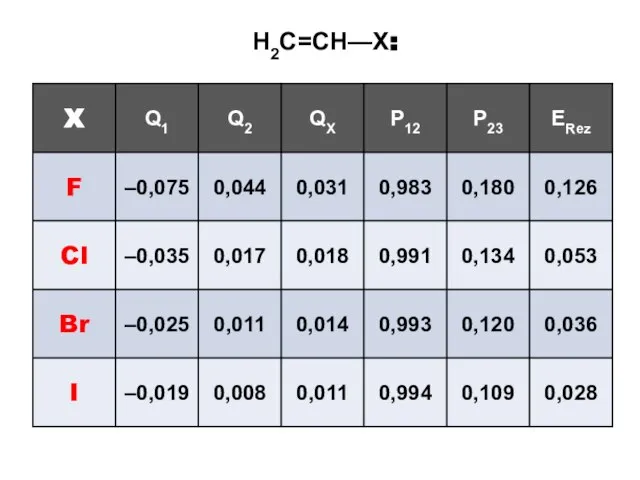
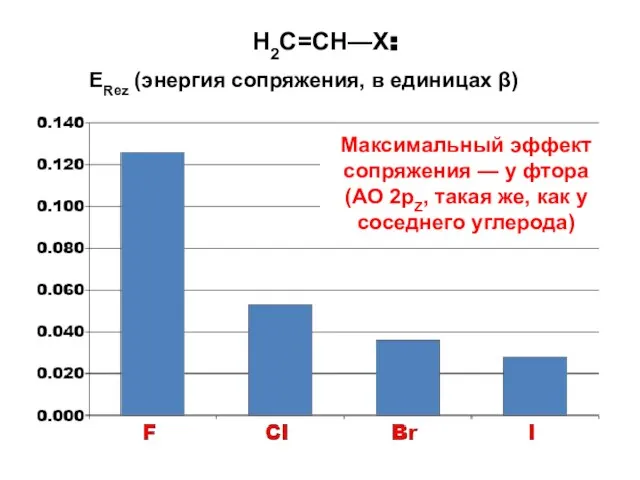
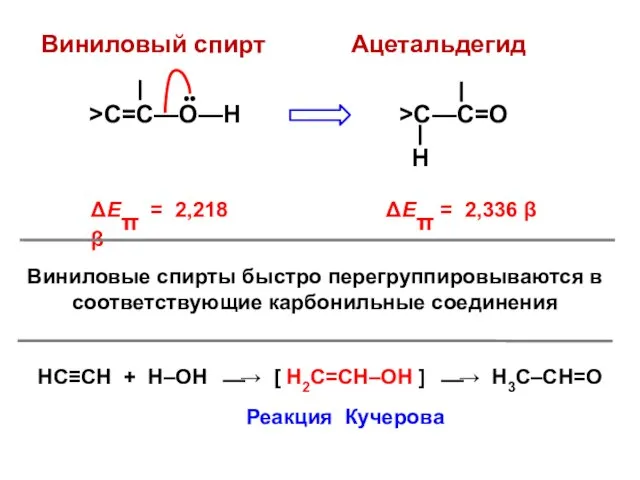
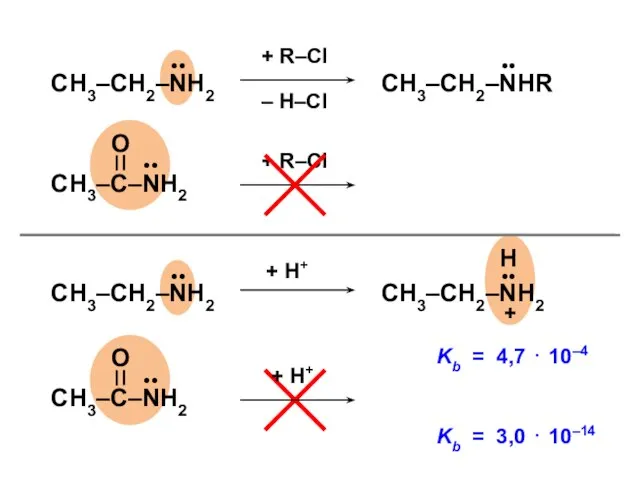
- 128. H2C=CH—X:
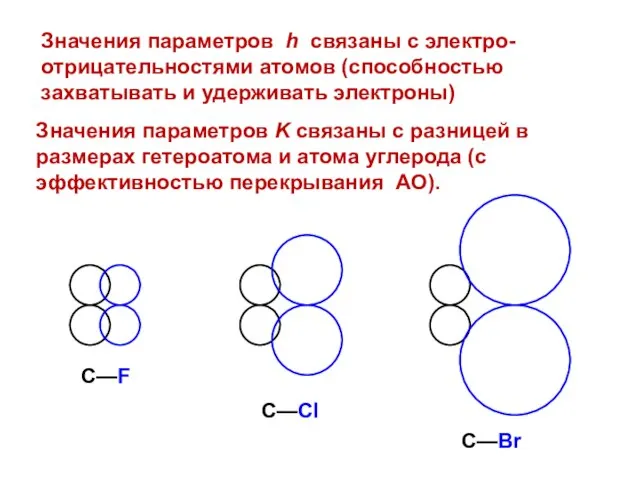
- 129. Значения параметров K связаны с разницей в размерах гетероатома и атома углерода (с эффективностью перекрывания АО).
- 130. H2C=CH—X: ERez (энергия сопряжения, в единицах β) Максимальный эффект сопряжения — у фтора (АО 2pZ, такая
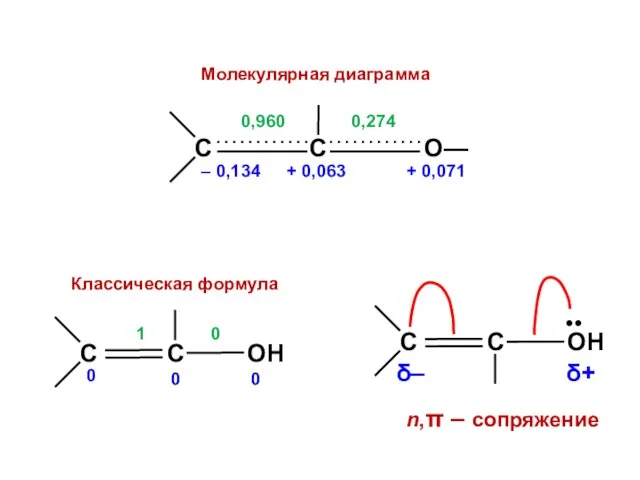
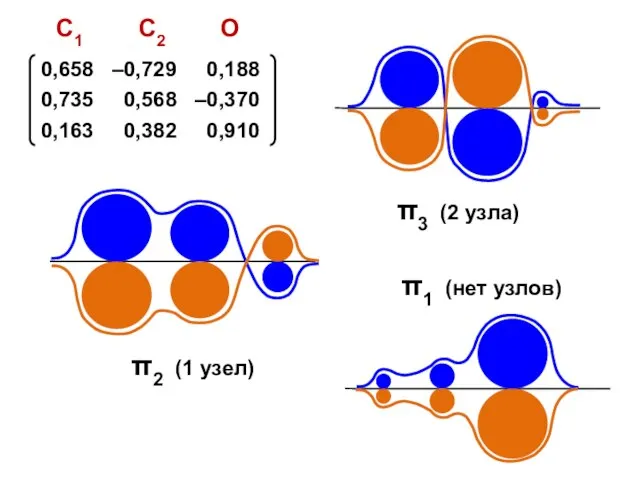
- 131. Виниловый спирт >C=C—О—Н h = 2,0 K = 0,8 Det = Х 3 + 2Х 2
- 132. nC1 = 1,134 no = 1 Q = – 0,134 nC2 = 0,937 no = 1
- 133. δ+ δ–
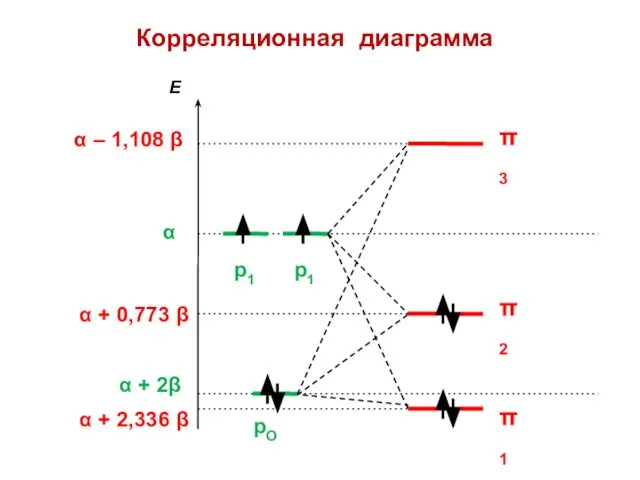
- 135. Корреляционная диаграмма
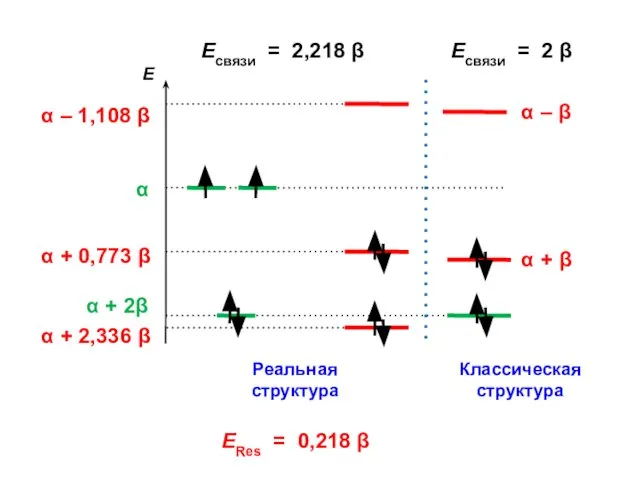
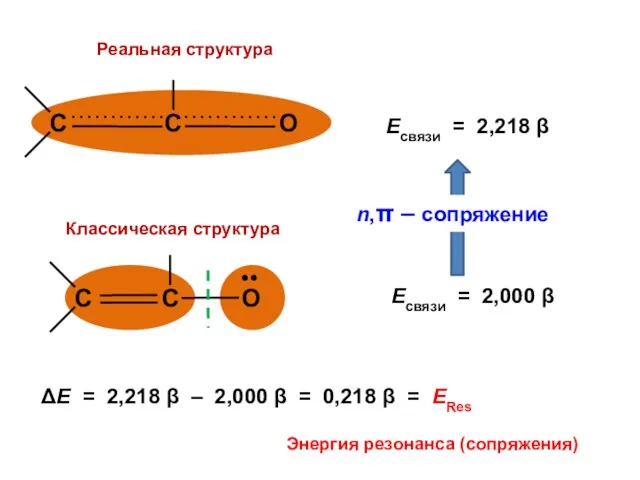
- 136. Есвязи = 2,218 β Есвязи = 2 β ERes = 0,218 β
- 137. ΔЕ = 2,218 β – 2,000 β = 0,218 β = ЕRes Энергия резонанса (сопряжения)
- 138. ΔЕπ = 2,336 β Виниловый спирт >C=C—О—Н •• Ацетальдегид >C—C=О Н ΔЕπ = 2,218 β Виниловые
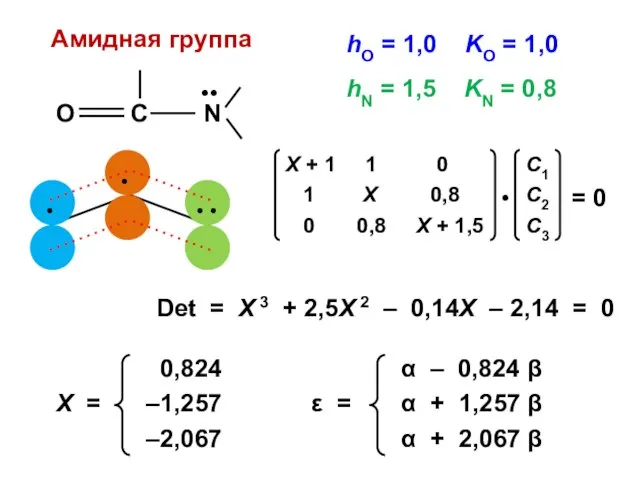
- 139. hO = 1,0 KO = 1,0 Det = Х 3 + 2,5Х 2 – 0,14Х –
- 140. nO = 1,575 no = 1 Q = – 0,575 nC = 0,592 no = 1
- 141. δ+ δ–
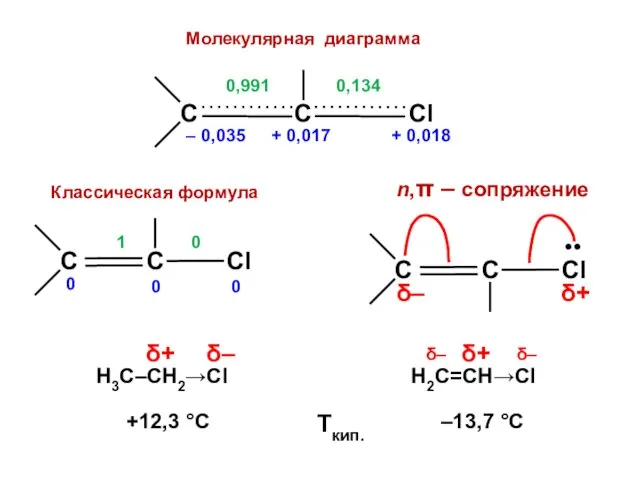
- 143. ΔЕ = 2,642 β – 2,236 β = 0,306 β = ЕRes (для винилхлорида ЕRes =
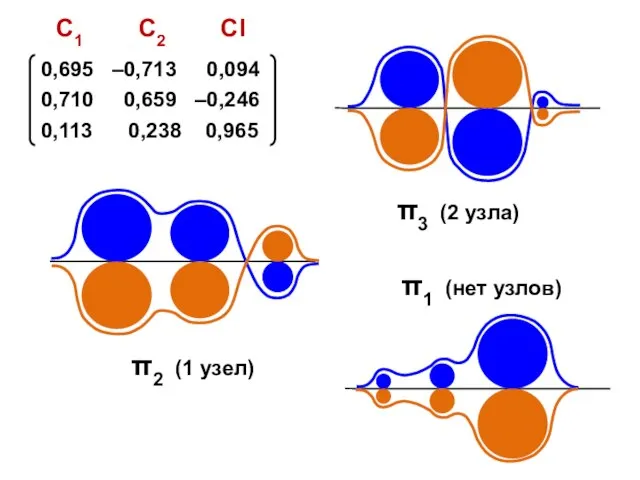
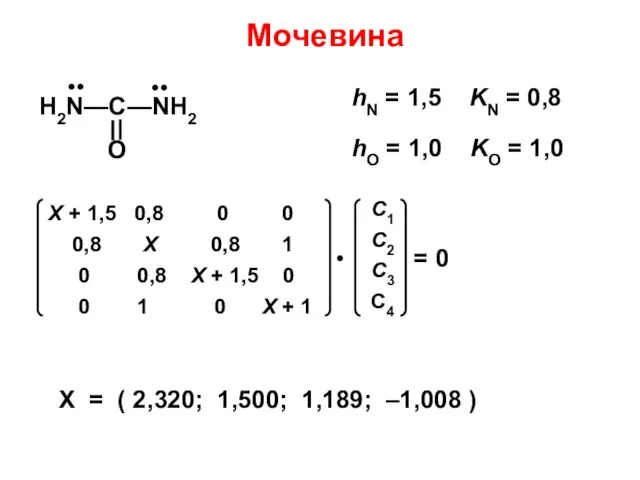
- 145. Мочевина X = ( 2,320; 1,500; 1,189; –1,008 )
- 146. nN1 = 1,860 no = 2 Q = + 0,140 nC = 0,622 no = 1
- 147. •• •• n-π-сопряжение
- 148. Корреляционная диаграмма Eсв. = 3,000 β
- 149. ERez = 0,764 β ( для амидной группы 0,306 β ) Классическая структура
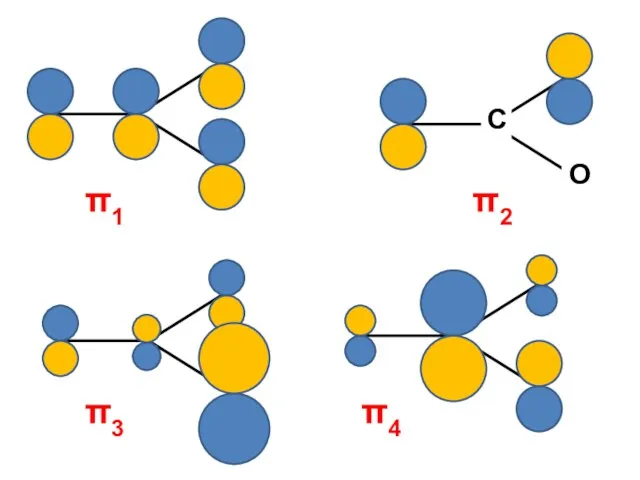
- 150. π1 π2 π3 π4 О С
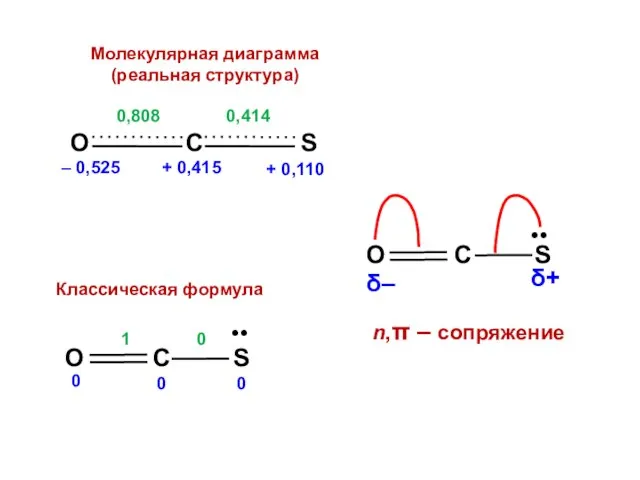
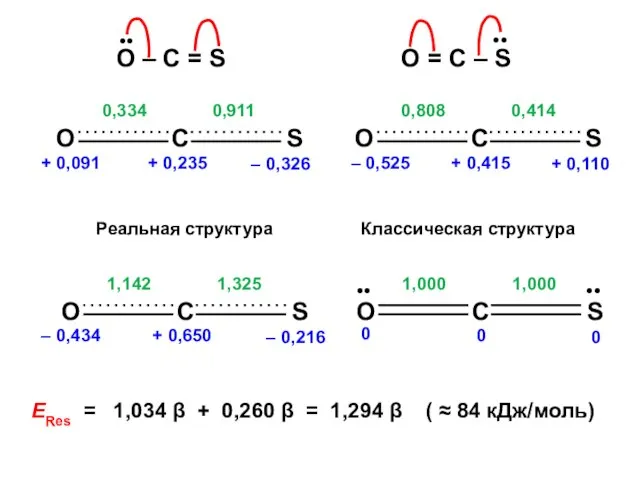
- 151. Сероокись углерода O = С = S
- 152. hO = 2,0 KO = 0,8 Det = Х 3 + 2,4Х 2 – 0,84Х –
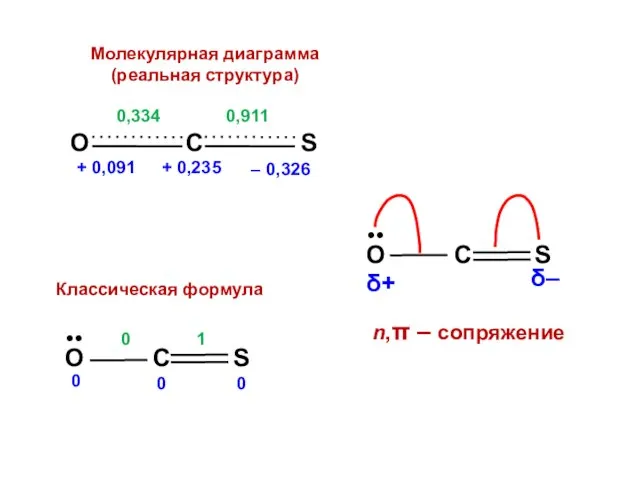
- 153. nO = 1,909 no = 2 Q = + 0,091 nC = 0,765 no = 1
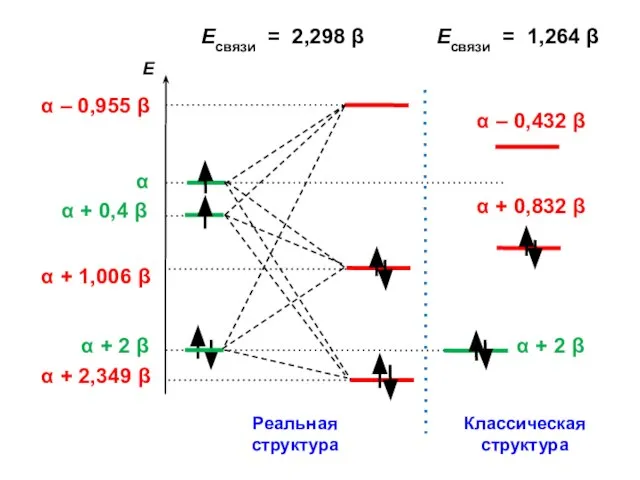
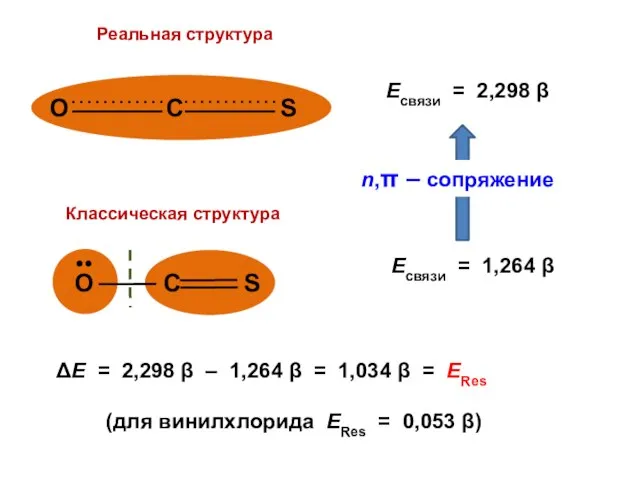
- 155. Есвязи = 2,298 β Есвязи = 1,264 β
- 156. ΔЕ = 2,298 β – 1,264 β = 1,034 β = ЕRes (для винилхлорида ЕRes =
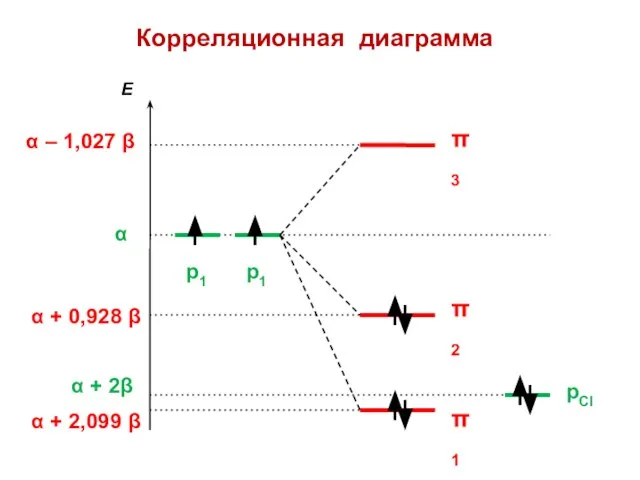
- 157. hO = 1,0 KO = 1,0 Det = Х 3 + 2,3Х 2 – 0,06Х –
- 158. nO = 1,525 no = 1 Q = – 0,525 nC = 0,585 no = 1
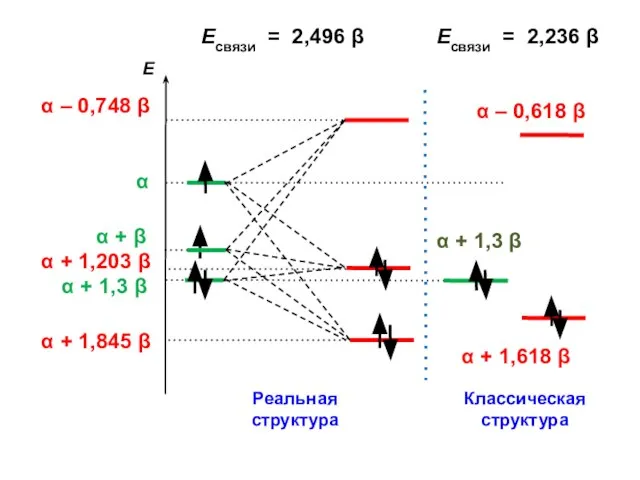
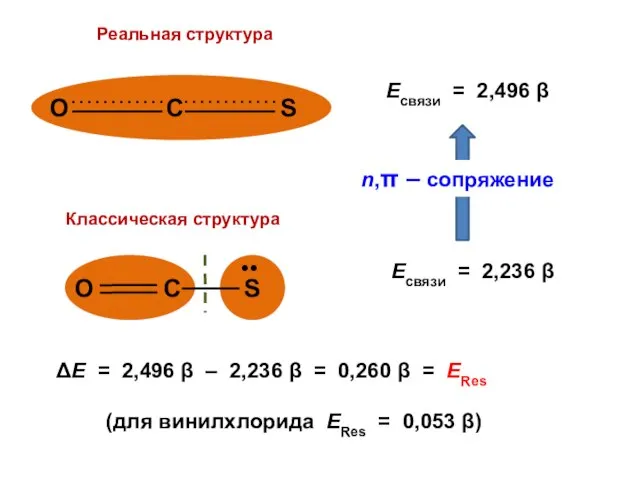
- 160. Есвязи = 2,496 β Есвязи = 2,236 β
- 161. ΔЕ = 2,496 β – 2,236 β = 0,260 β = ЕRes (для винилхлорида ЕRes =
- 162. ЕRes = 1,034 β + 0,260 β = 1,294 β ( ≈ 84 кДж/моль)
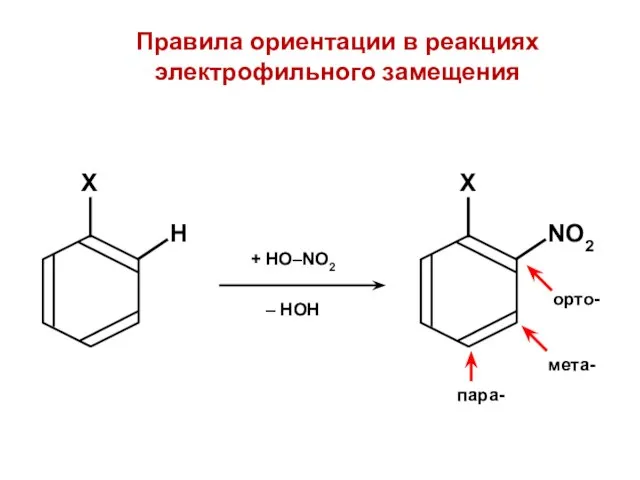
- 163. Правила ориентации в реакциях электрофильного замещения
- 168. ••
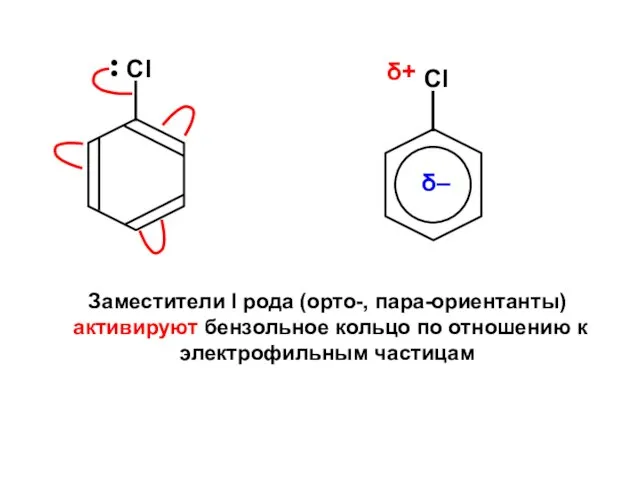
- 169. Заместители I-го рода (орто-, пара-ориентанты) Заместители II-го рода (мета-ориентанты)
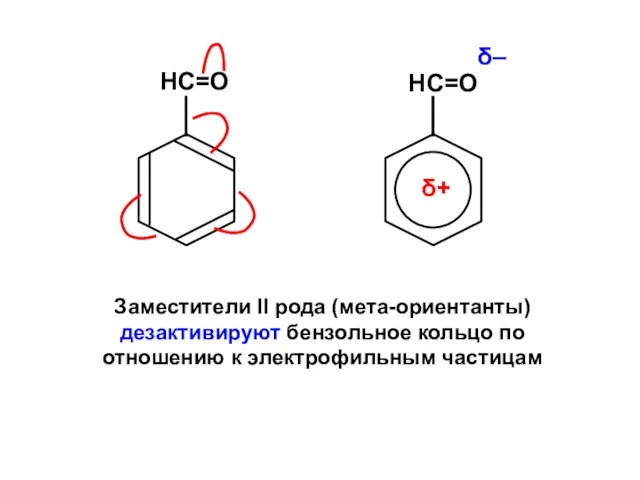
- 170. Заместители I рода (орто-, пара-ориентанты) активируют бензольное кольцо по отношению к электрофильным частицам
- 171. Заместители II рода (мета-ориентанты) дезактивируют бензольное кольцо по отношению к электрофильным частицам
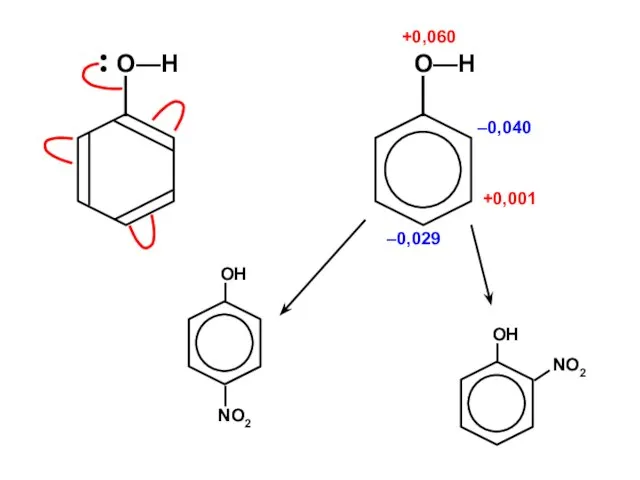
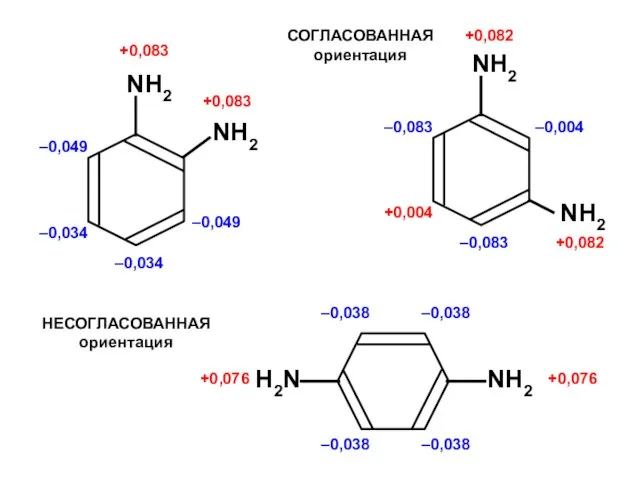
- 172. НЕСОГЛАСОВАННАЯ ориентация СОГЛАСОВАННАЯ ориентация
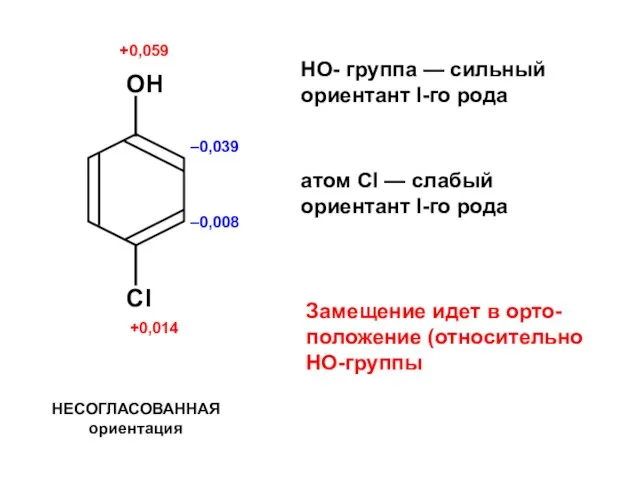
- 173. НЕСОГЛАСОВАННАЯ ориентация Замещение идет в орто-положение (относительно НО-группы
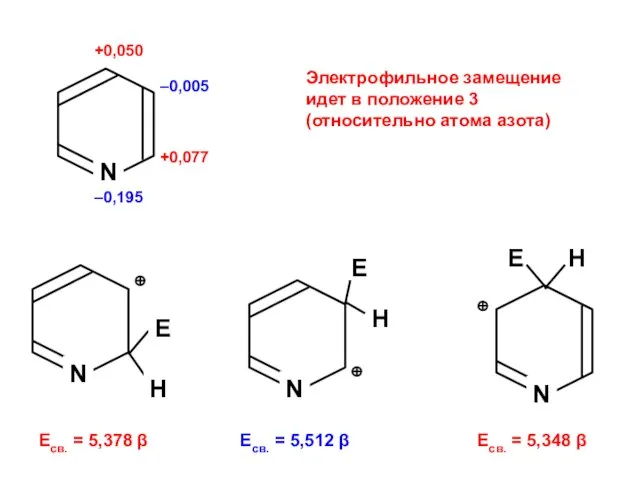
- 174. +0,077 +0,050 –0,195 –0,005 N Электрофильное замещение идет в положение 3 (относительно атома азота) Есв. =
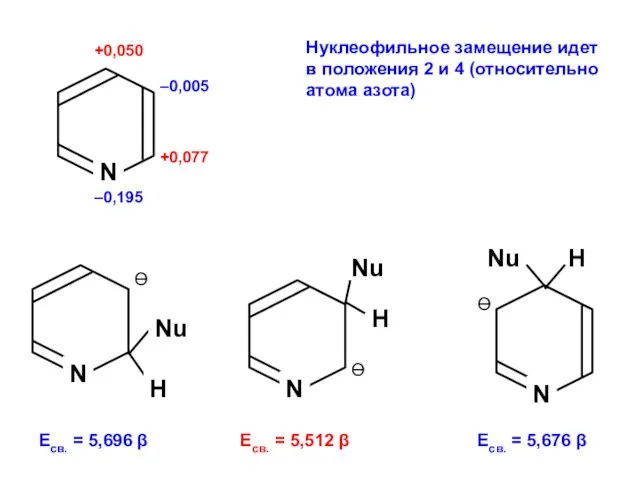
- 175. +0,077 +0,050 –0,195 –0,005 Нуклеофильное замещение идет в положения 2 и 4 (относительно атома азота) N
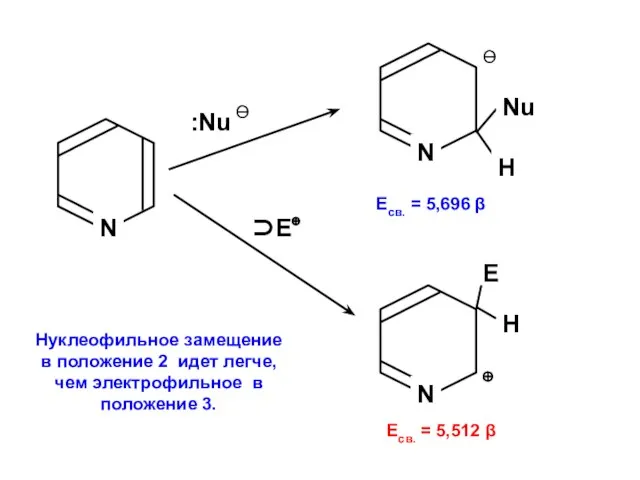
- 176. Нуклеофильное замещение в положение 2 идет легче, чем электрофильное в положение 3.
- 178. Есв. = 4,820 β Есв. = 4,454 β
- 179. Есв. = 4,448 β Есв. = 3,826 β
- 181. Задача 8.3.
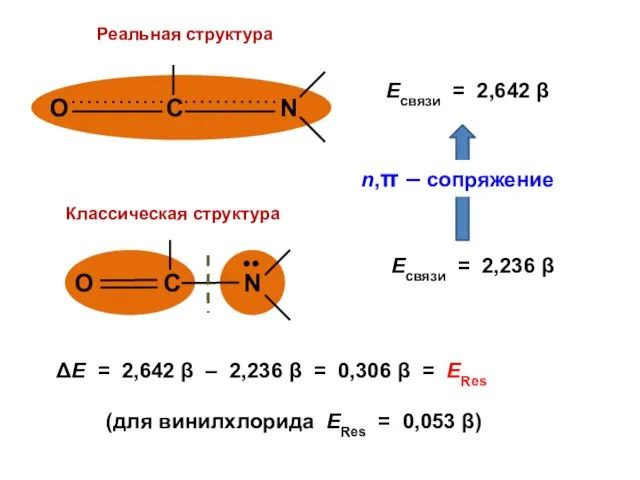
- 182. 1. Составить уравнение Хюккеля с учетом поправок на гетероатомы 2. По очереди подставить в это уравнение
- 183. 3. Решить полученные 4 экземпляра уравнения Хюккеля и из решений (предварительно пронормированных) составить атомно-молекулярную матрицу:
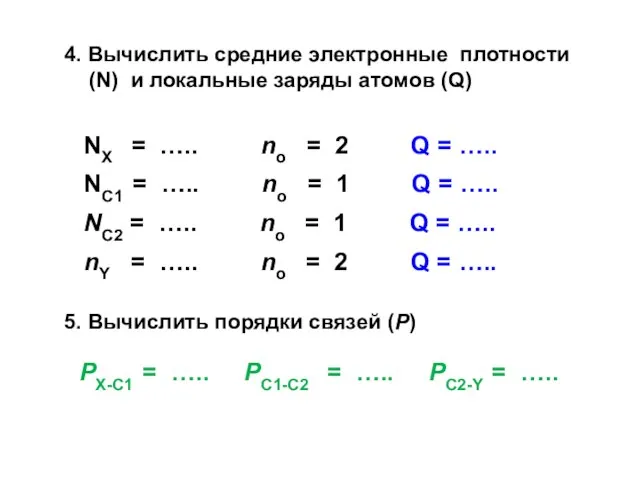
- 184. NX = ….. no = 2 Q = ….. NC1 = ….. no = 1 Q
- 185. 6. Вычислить орбитальные энергии по формуле: εi = α – β ⋅ Xi 7. Построить энергетические
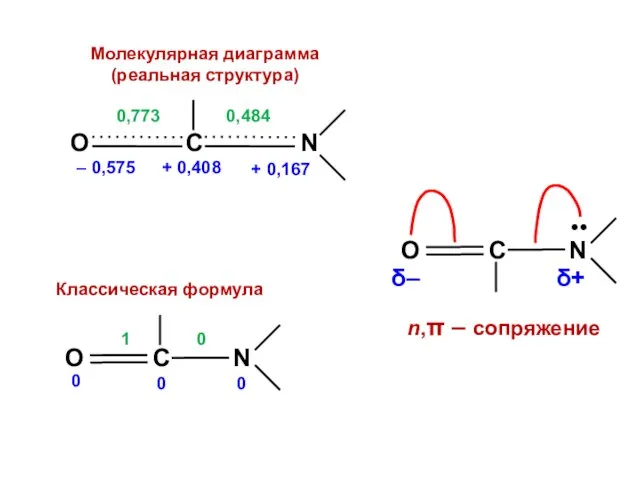
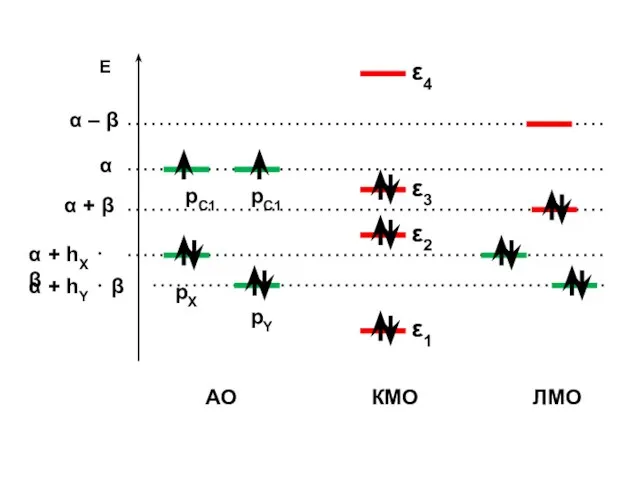
- 186. Е α + hX ⋅ β рС1 рС1 рX рY α α + hY ⋅ β
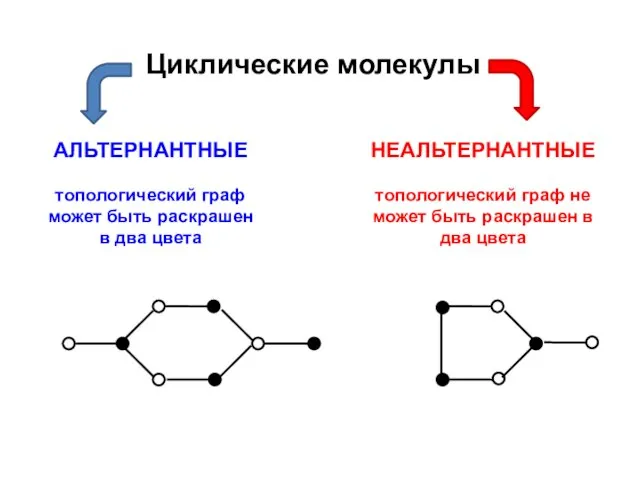
- 187. Циклические молекулы
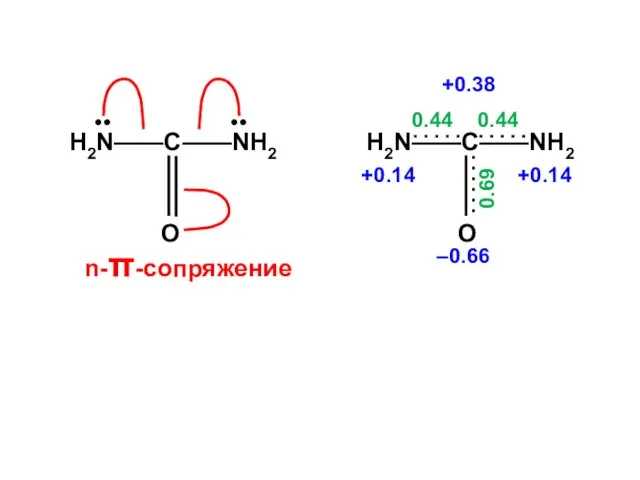
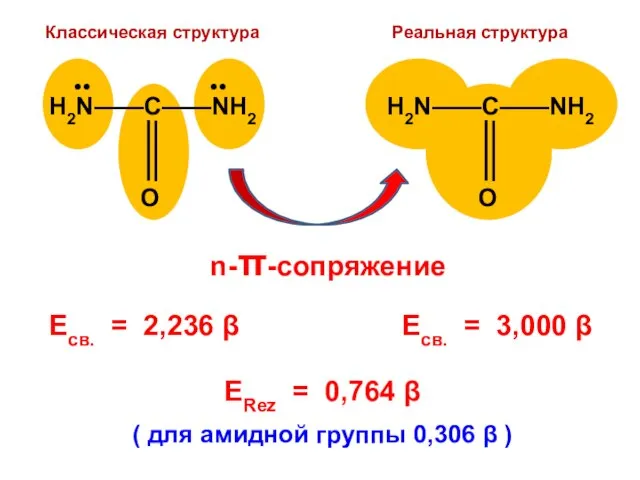
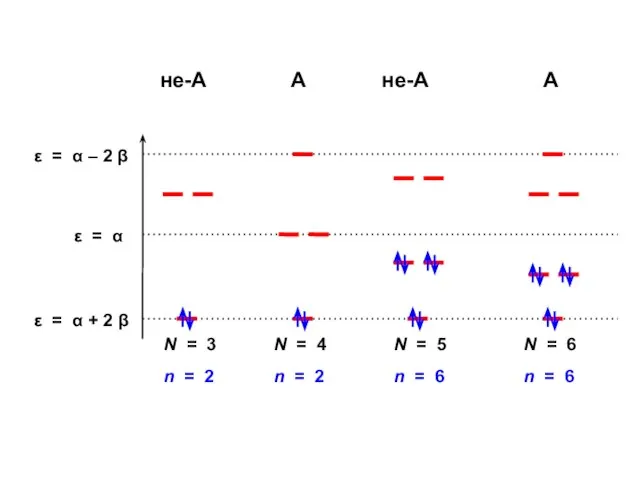
- 188. Для альтернантных молекул всегда имеются дважды вырожденные уровни, которые располагаются симметрично, относительно нулевого уровня с ε
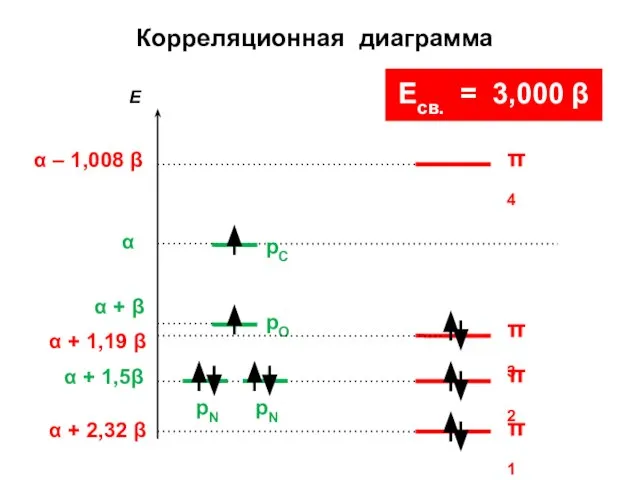
- 189. не-А не-А А А
- 190. Для альтернантных молекул электрические заряды атомов равны нулю; такие молекулы не поляризованы и их дипольный момент
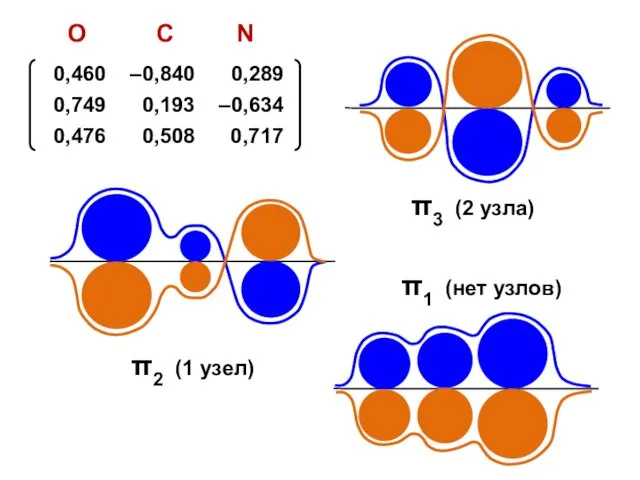
- 191. Для неальтернантных молекул электрические заряды атомов не равны нулю; такие молекулы поляризованы и их дипольный момент
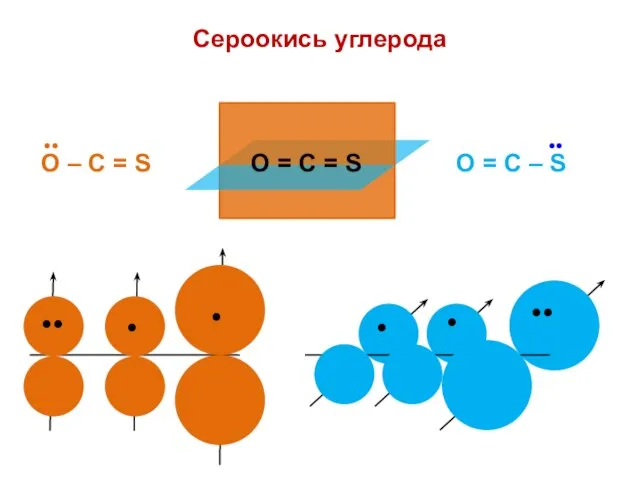
- 196. Скачать презентацию




























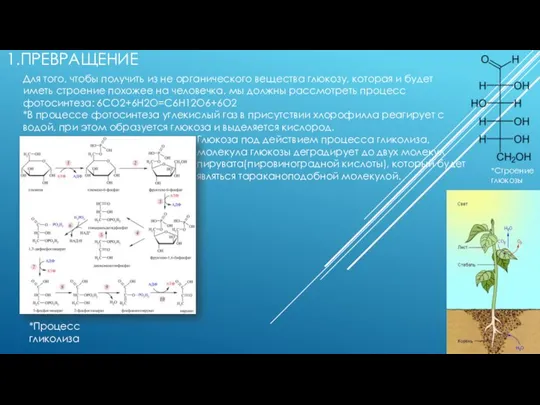 Превращение из не органического вещества в глюкозу
Превращение из не органического вещества в глюкозу Сложные вещества оксиды
Сложные вещества оксиды Стехиометрические законы химии
Стехиометрические законы химии Нефть. Черное золото или черная смерть
Нефть. Черное золото или черная смерть Hydroxidy. Vlastnosti
Hydroxidy. Vlastnosti Презентация на тему Водород
Презентация на тему Водород  Вещества простые и сложные
Вещества простые и сложные Жидкокристаллический эластомер как роторный актуатор
Жидкокристаллический эластомер как роторный актуатор Основы стереохимии
Основы стереохимии Нефть. Состав, свойства, переработка
Нефть. Состав, свойства, переработка Теория химического строения (ТХС). Предпосылки создания
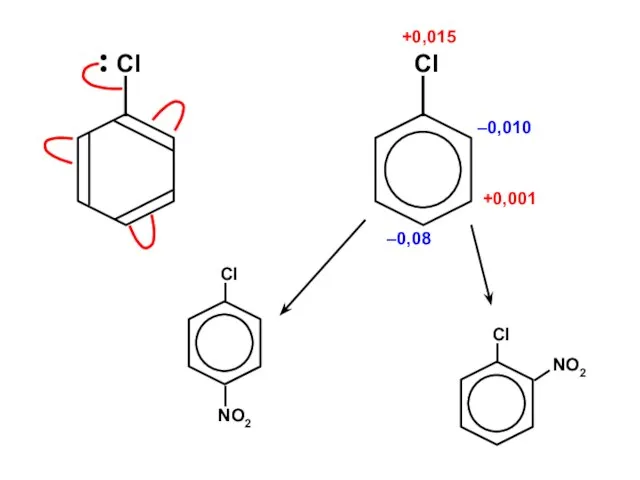
Теория химического строения (ТХС). Предпосылки создания Химическая связь и строение молекул
Химическая связь и строение молекул Кислоты. Общая формула кислот
Кислоты. Общая формула кислот Генетическая связь неорганических соединений
Генетическая связь неорганических соединений Контрольная работа №1
Контрольная работа №1 Комплексные соединения
Комплексные соединения Состав и свойства нефти. Химический состав нефтяной смеси
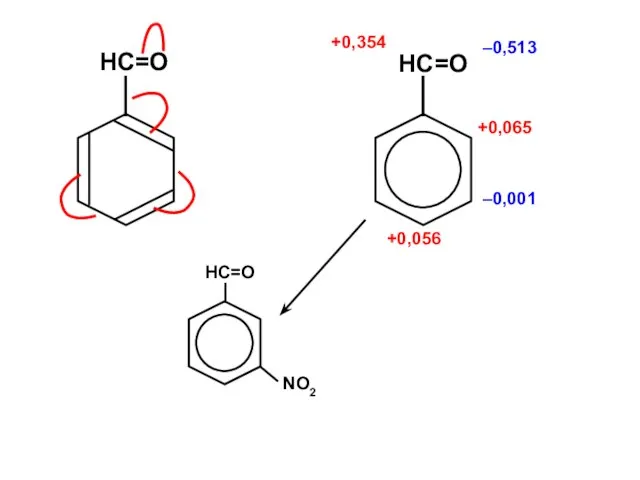
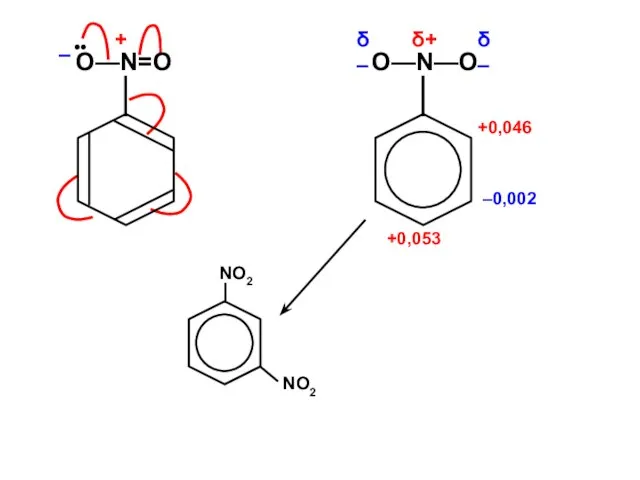
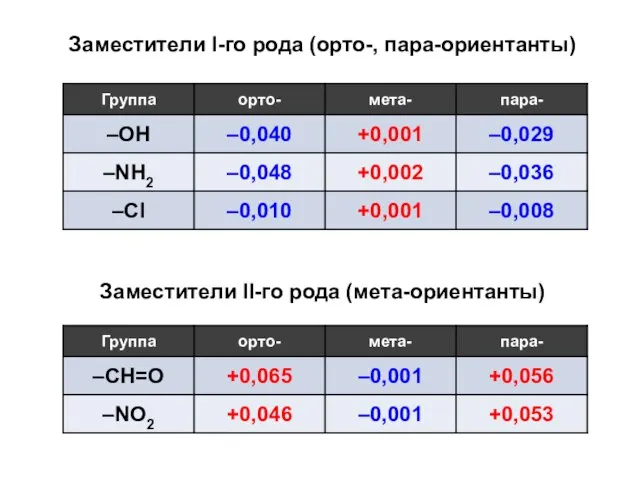
Состав и свойства нефти. Химический состав нефтяной смеси Основания, их состав и название
Основания, их состав и название Бикомпонентные покрытия
Бикомпонентные покрытия Фуллерены
Фуллерены Ароматические углеводороды
Ароматические углеводороды Алканы. Этан - C₂H₆
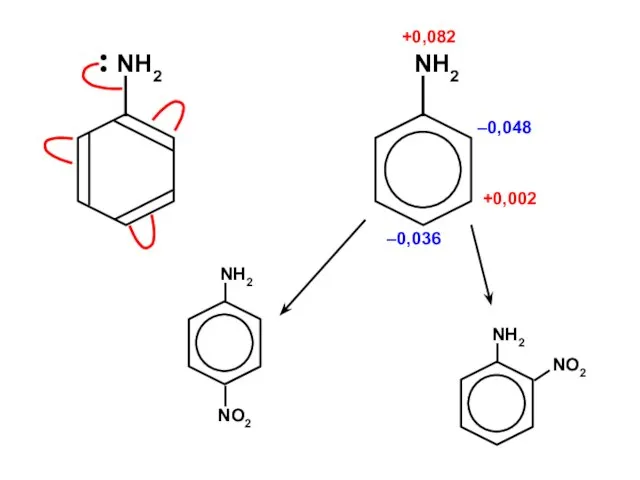
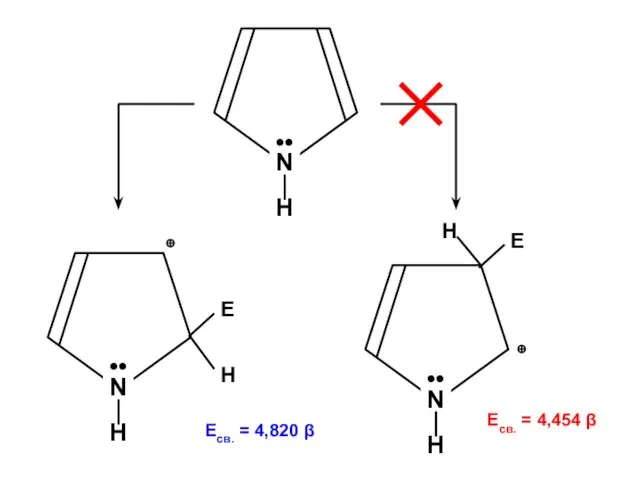
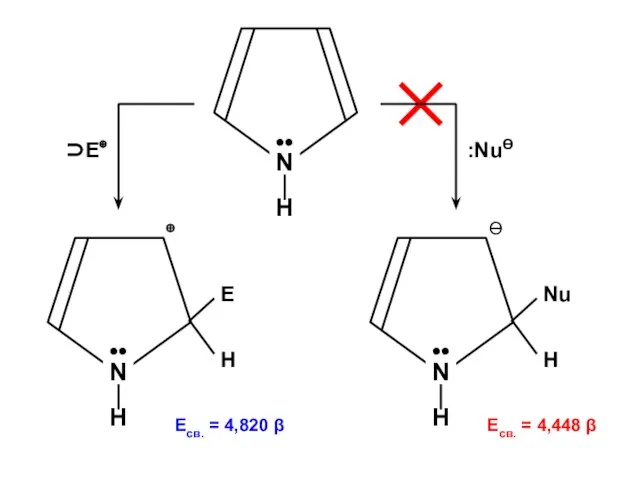
Алканы. Этан - C₂H₆ Галогены
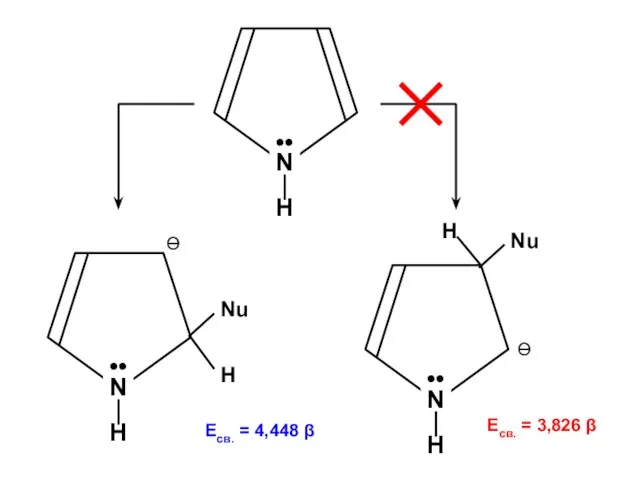
Галогены Химическая лаборатория
Химическая лаборатория ізомери
ізомери Презентация на тему Кристаллические решетки 9 класс
Презентация на тему Кристаллические решетки 9 класс  задачи
задачи Уравнение материального баланса технологического процесса. (Лекция 3)
Уравнение материального баланса технологического процесса. (Лекция 3)