Содержание
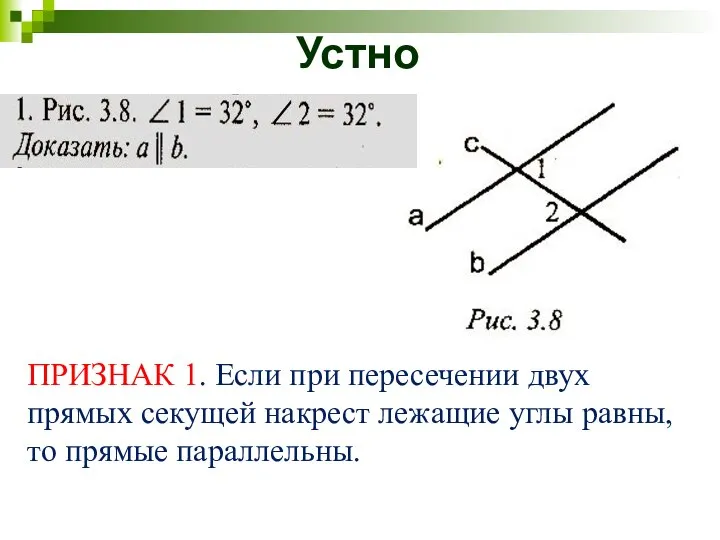
- 2. Устно ПРИЗНАК 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
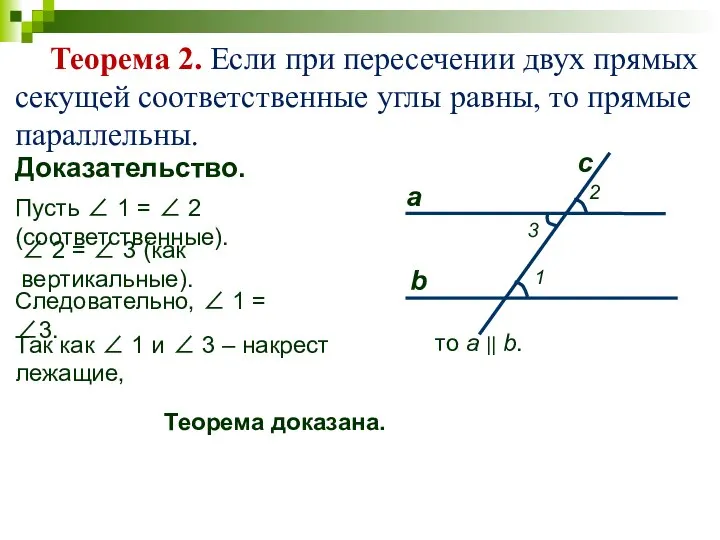
- 3. Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Доказательство. Следовательно,
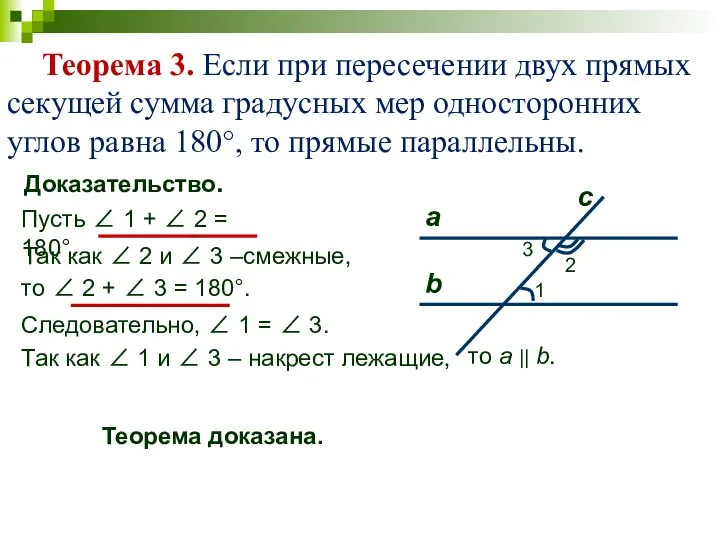
- 4. Теорема 3. Если при пересечении двух прямых секущей сумма градусных мер односторонних углов равна 180°, то
- 5. Признаки параллельности двух прямых Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые
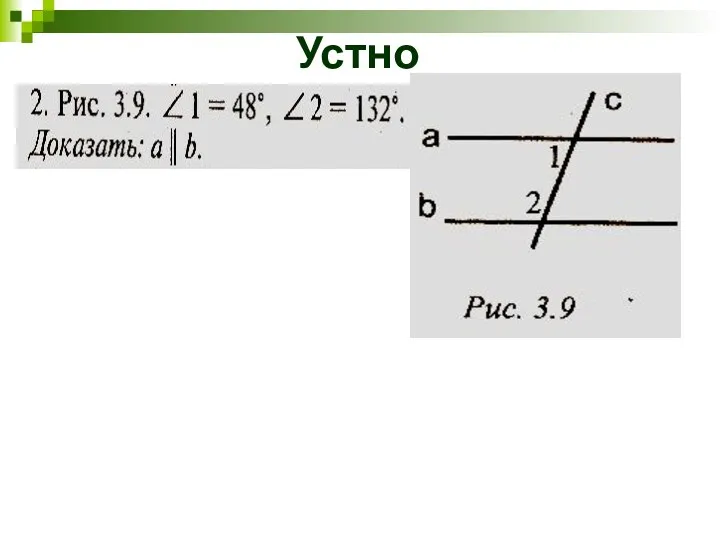
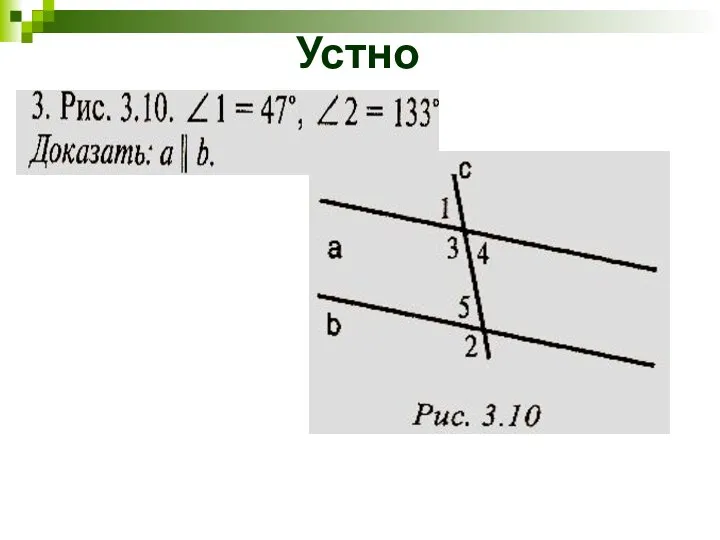
- 6. Устно
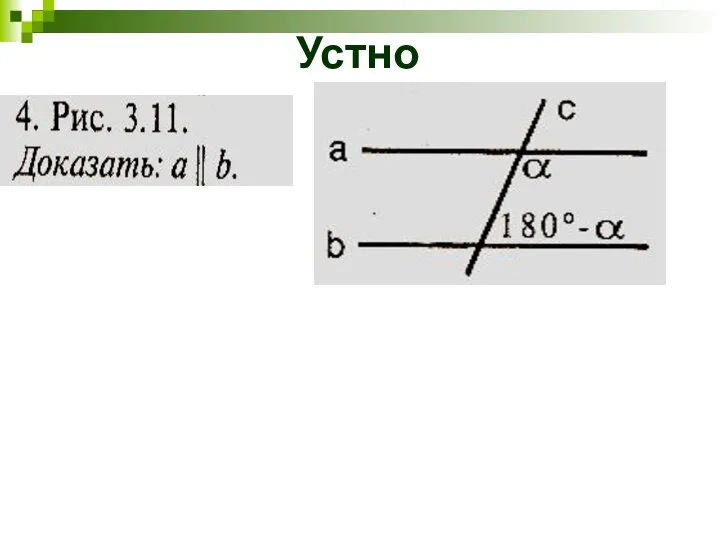
- 7. Устно
- 8. Устно
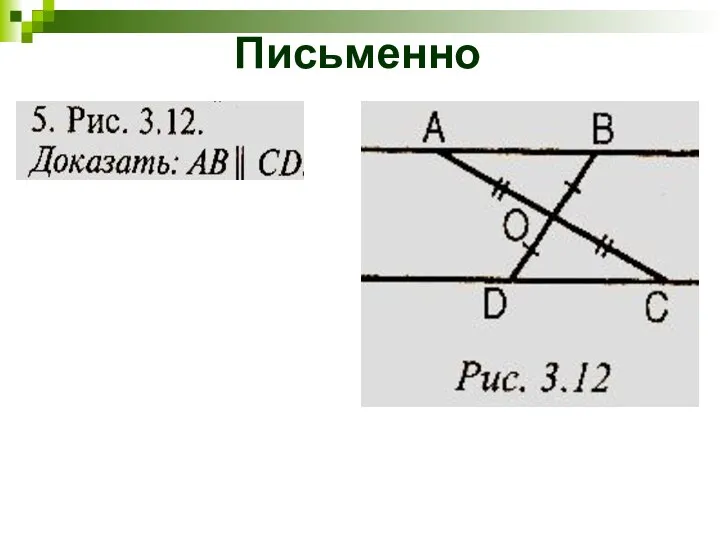
- 9. Письменно
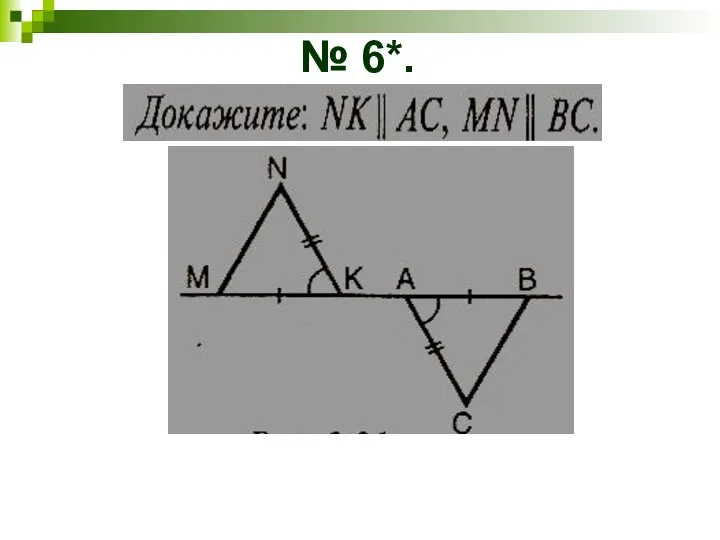
- 10. № 6*.
- 12. Скачать презентацию

 Презентация по математике "Праздник чисел «5 плюс »" -
Презентация по математике "Праздник чисел «5 плюс »" -  Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Старинные меры длины
Старинные меры длины Статистическая проверка гипотез
Статистическая проверка гипотез Сбережение водных ресурсов. Решение задач на сравнение величин
Сбережение водных ресурсов. Решение задач на сравнение величин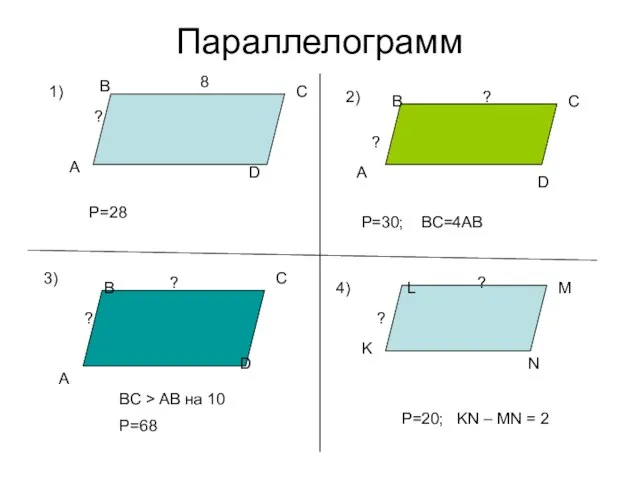 Параллелограмм
Параллелограмм Окружность Аполлония
Окружность Аполлония Формирование и развитие познавательных УУД на уроках математики
Формирование и развитие познавательных УУД на уроках математики Интерактивный плакат Треугольник
Интерактивный плакат Треугольник Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями
Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями Тест по теме Окружность
Тест по теме Окружность Презентация на тему Показательная функция: свойства, график
Презентация на тему Показательная функция: свойства, график  Интерактивный пазл
Интерактивный пазл Маршрутный лист группы
Маршрутный лист группы Credit and exam
Credit and exam Квадратные уравнения. Лекция
Квадратные уравнения. Лекция Система быстрого счёта в уме Якова Трахтенберга. Занятия 3
Система быстрого счёта в уме Якова Трахтенберга. Занятия 3 Скалярное произведение векторов
Скалярное произведение векторов Рациональные и действительные числа. Приближенные выражения
Рациональные и действительные числа. Приближенные выражения Планиметрия. Задачи
Планиметрия. Задачи Задача на внимание. 5 класс
Задача на внимание. 5 класс 3.7. Непрерывность функции
3.7. Непрерывность функции Четырехугольники
Четырехугольники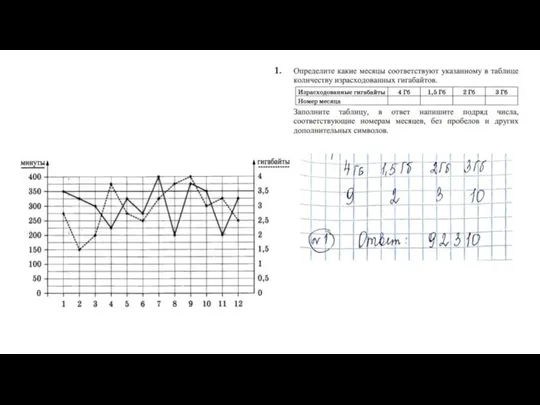 Решение задач
Решение задач Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Презентация на тему Функция у=к/х, её свойства и график
Презентация на тему Функция у=к/х, её свойства и график  Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Рисуем по координатам
Рисуем по координатам