Слайд 2План исследования функции и построения графика
1. Найти область определения D(f) функции f(x).
2.

Найти область значений E(f) (если это возможно вначале, часто E(f) можно указать только по результатам исследования).
3. Исследовать функцию на четность.
4. Исследовать функцию на периодичность.
5. Найти точки пересечения с осью Ox (нули функции) и точки пересечения с осью Oy.
6. Найти промежутки знакопостоянства функции.
7. Исследовать функцию на непрерывность, дать классификацию разрывов.
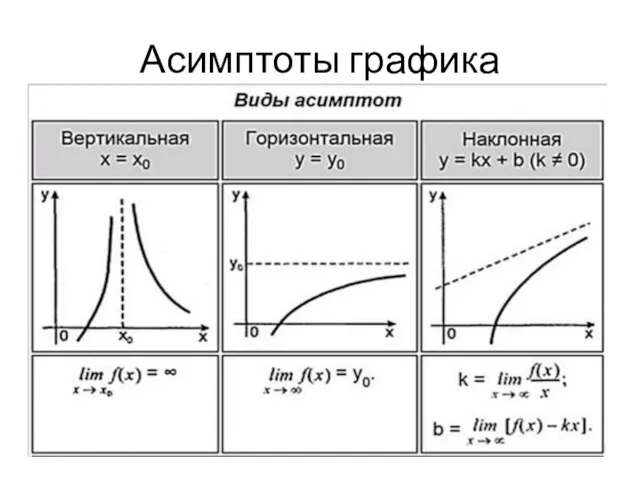
8. Найти асимптоты графика функции (вертикальную, наклонную, горизонтальную).
9. Исследовать функцию на монотонность и экстремум.
10. Исследовать график функции на выпуклость, вогнутость, перегиб.
11. Построить график функции.
Слайд 3Нахождение области определения функции
Обозначение: D(f)
Определение: ООФ – это множество чисел, на

котором задается функция. Если ООФ не указана, то считается, что ООФ состоит из всех значений х, при которых функция определена.
Слайд 4Какие могут быть препятствия для х?

Слайд 5Исследование функции на четность
Условие четности:
f(x)=f(-x); график симметричен относительно ОY.
Условие нечетности:
f(-x)= -

f(x); график симметричен относительно начала координат.
Если эти условия не выполняются, то функция общего вида.
Слайд 6Исследование функции на периодичность

Слайд 7Пересечение с осями координат
Нули функции (пересечение с ОХ)
Решаем уравнение f(х)=0
Пересечение с

ОУ
Находим f(0)
Слайд 8Промежутки знакопостоянства функции
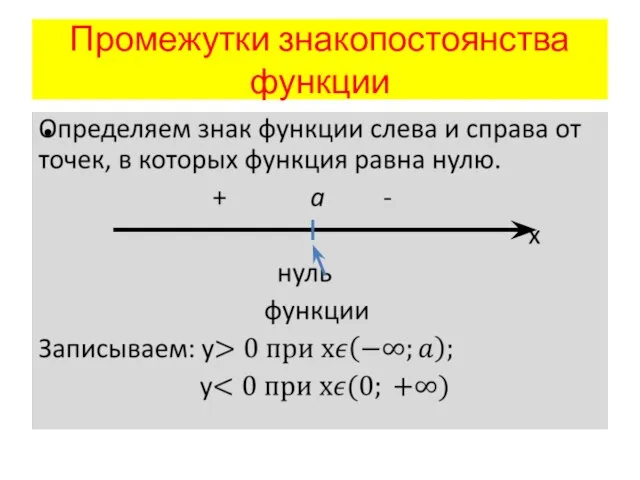
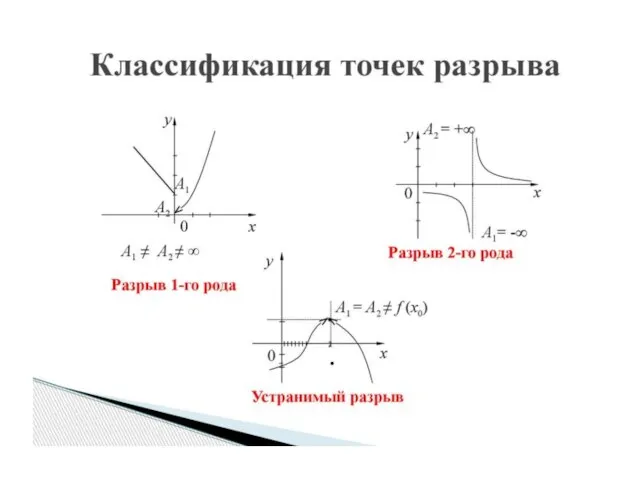
Слайд 9Исследование функции на непрерывность

Слайд 12Функция непрерывна на всей числовой прямой кроме точки х=-1 , в которой
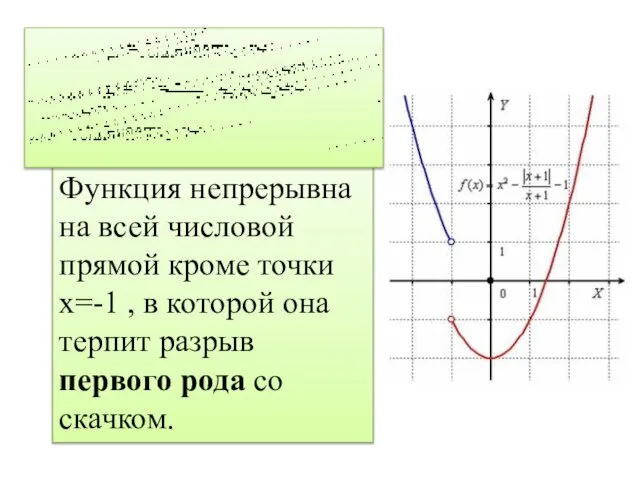
она терпит разрыв первого рода со скачком.
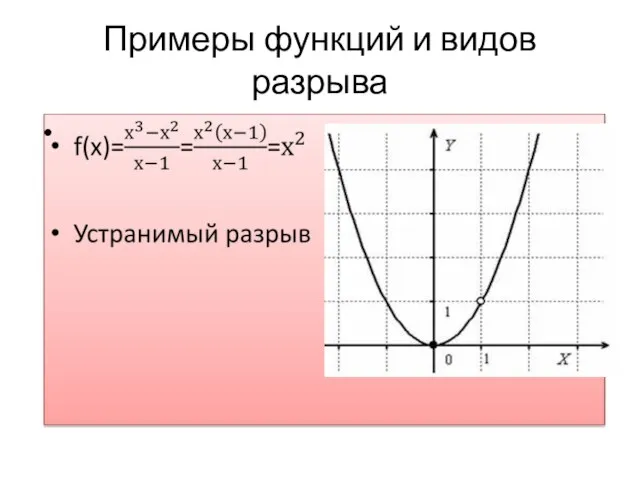
Слайд 13Функция непрерывна на всей числовой прямой, кроме точки х=-1 , в которой
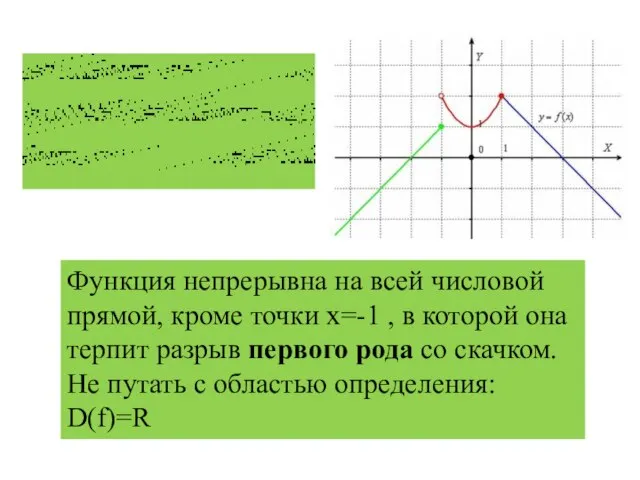
она терпит разрыв первого рода со скачком.
Не путать с областью определения: D(f)=R
Слайд 14Функция непрерывна на всей числовой
прямой кроме точки х=1,
в которой она
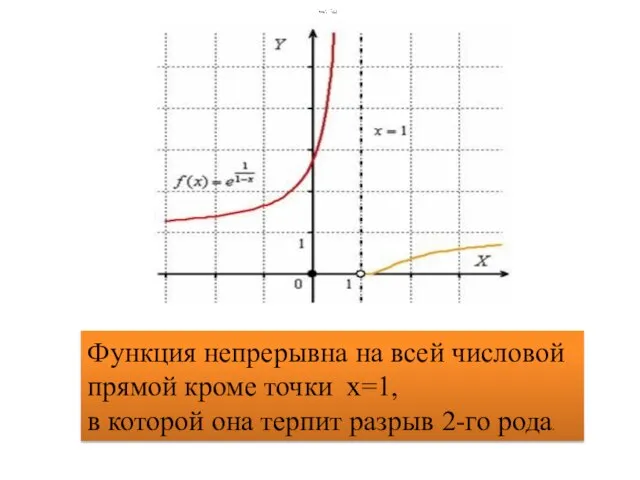
терпит разрыв 2-го рода.
Слайд 16Исследование на монотонность и экстремумы
Найти производную функции.
Приравнять ее к 0.
Справа и слева

от точек, в которых производная равна нулю, определить знак производной.
Найти промежутки возрастания и убывания функции. Если производная положительна, то функция возрастает; если отрицательна, то убывает.
Найти точки экстремума (или точки перегиба)
Найти значение функции в точках экстремума или точках перегиба (для построения графика).
Слайд 17Исследование на выпуклость, вогнутость, перегибы
Необходимо найти вторую производную функции и приравнять ее

к нулю. Если вторая производная больше нуля, то на этом промежутке выпуклость вниз, если меньше – выпуклость вверх. Точка, в которой вторая производная равна нулю, является точкой перегиба. В ней меняется направление выпуклости.
Слайд 18Построение графика
В процессе исследования функции мы получили следующие точки графика:
Точки пересечения с

осями
Точки максимума и минимума
Точки перегиба
Точки разрыва














 Объемы многогранников и тел вращения. Практическая работа
Объемы многогранников и тел вращения. Практическая работа Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Учимся писать цифры
Учимся писать цифры Властивості задачі лінійного програмування
Властивості задачі лінійного програмування Вычитание смешанных чисел
Вычитание смешанных чисел Определенный интеграл. Решение примеров на нахождение первообразных и интегралов
Определенный интеграл. Решение примеров на нахождение первообразных и интегралов Метрологические основы анализа
Метрологические основы анализа Симметрия в Алтайских орнаментах на примере алтайских костюмов
Симметрия в Алтайских орнаментах на примере алтайских костюмов Углы с соответственно параллельными или перпендикулярными сторонами
Углы с соответственно параллельными или перпендикулярными сторонами Математику нельзя изучать, наблюдая, как это делает сосед (задачи)
Математику нельзя изучать, наблюдая, как это делает сосед (задачи)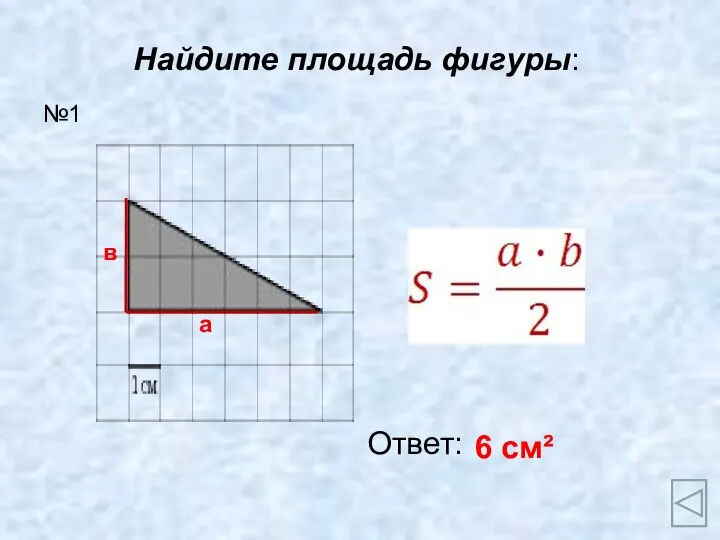 Формулы площадей
Формулы площадей Неполное квадратное уравнение
Неполное квадратное уравнение Применение производной в физике
Применение производной в физике Окружность. Касательная к окружности
Окружность. Касательная к окружности Шаблон презентации по математике
Шаблон презентации по математике Дивергентные математические задачи как средство развития креативности мышления у младших школьников
Дивергентные математические задачи как средство развития креативности мышления у младших школьников Обратная матрица
Обратная матрица Виды треугольников
Виды треугольников Круг, окружность, длина окружности. 6 класс
Круг, окружность, длина окружности. 6 класс Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ
Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ Презентация на тему Средняя линия
Презентация на тему Средняя линия  Домашнее задание . Подготовка к контрольной работе
Домашнее задание . Подготовка к контрольной работе Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Презентация на тему Функция. График функции.
Презентация на тему Функция. График функции.  Первые цифры
Первые цифры Алгоритм вычисления алгебраических выражений
Алгоритм вычисления алгебраических выражений Решение задач и примеров
Решение задач и примеров Марафон по математике. Задание 13
Марафон по математике. Задание 13