Производная и дифференциал функции

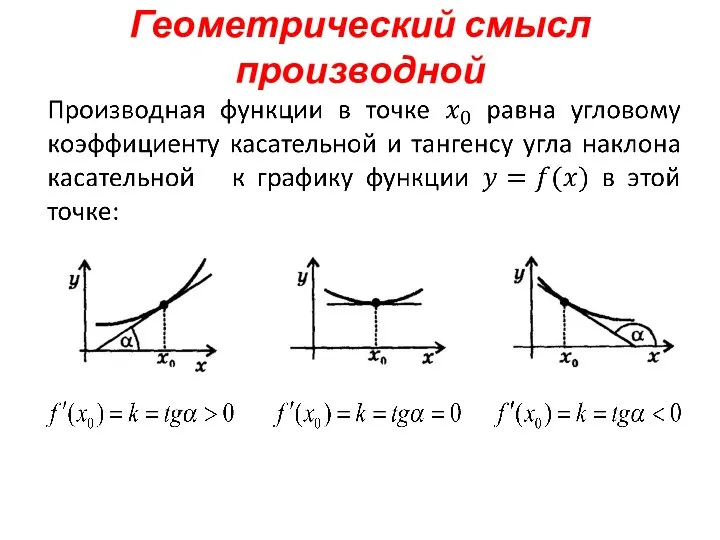
Геометрический смысл производной

Решение:
y’(x)= 2x-1
k= y’ (1)= 2*1-1= 1
k =tgα= 1, значит α=45º

Уравнение касательной

Алгоритм для составления уравнения касательной:
Найти значение функции в точке хₒ
Найти производную функции f’(x)
Найти значение производной функции в точке хₒ
Найденные значения подставляем в уравнение касательной

Решение:
f (хₒ)= (-2)³-3* (-2)+1=-1
f’(x)=3x²-3
f’(хₒ)= f’(-2)= 3* (-2)²-3=9
y= -1+9(x+2)= 9x+17

Механический смысл производной
Механический смысл производной заключается в том, что скорость материальной точки равна производной закона пути движения этой точки:
Скорость – это производная пути по времени.
Ускорение- это производная скорости
a(t)= ν‘ (t)= s‘‘(t)

Таблица производных сложных функций