Содержание
- 2. ТЕОРЕМА Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной
- 3. Доказательство: По условию функция y=f(x) дифференцируема и Тогда Пусть Δy - приращение независимой переменной y, не
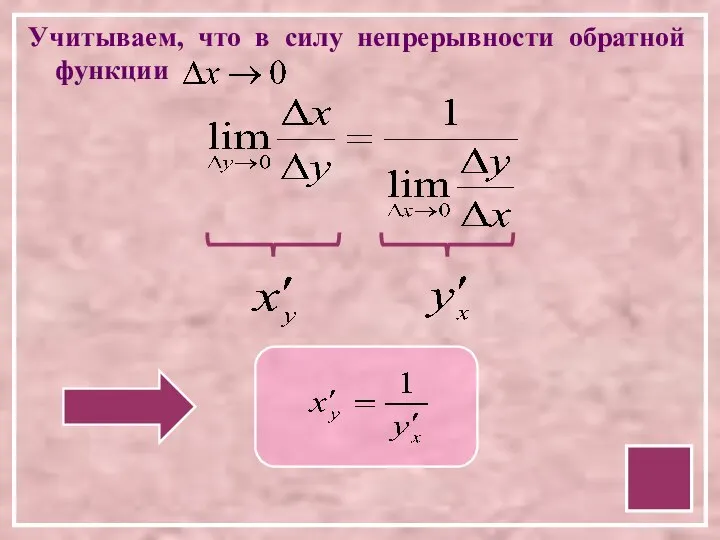
- 4. Учитываем, что в силу непрерывности обратной функции
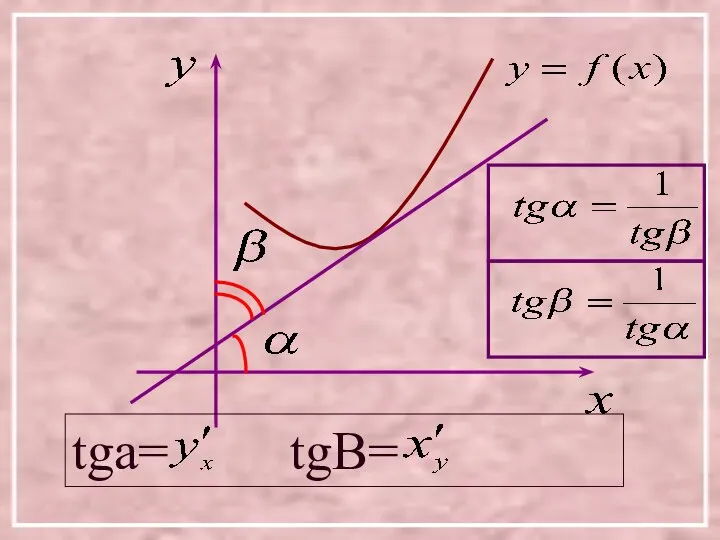
- 5. Эта формула имеет простой геометрический смысл. Если есть тангенс угла наклона касательной к кривой y=f(x) к
- 6. tga= tgB=
- 8. Скачать презентацию



 Построение графика производной методом касательных
Построение графика производной методом касательных Теория статистики. Предмет, задачи, основные категории и понятия статистики
Теория статистики. Предмет, задачи, основные категории и понятия статистики Таблица сложения в пределах 20
Таблица сложения в пределах 20 Сложение десятичных дробей
Сложение десятичных дробей Ментальная арифметика
Ментальная арифметика Площадь параллелограмма
Площадь параллелограмма Неравенства. Решить систему неравенств
Неравенства. Решить систему неравенств Равнобокая трапеция из бумаги. Работа ножницами
Равнобокая трапеция из бумаги. Работа ножницами Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат
Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат Мишка. Тренажёр - раскраска
Мишка. Тренажёр - раскраска Учимся писать цифры
Учимся писать цифры Соотношения между сторонами и углами в прямоугольном треугольнике
Соотношения между сторонами и углами в прямоугольном треугольнике Презентация на тему Цилиндр
Презентация на тему Цилиндр  Одночлен. Умножение
Одночлен. Умножение Векторно-координатный метод нахождения угла между плоскостями
Векторно-координатный метод нахождения угла между плоскостями Решение задач по теме Параллельность прямой и плоскости
Решение задач по теме Параллельность прямой и плоскости Решение практических задач с помощью арифметической прогрессии
Решение практических задач с помощью арифметической прогрессии Параллельные прямые. Свойства и признаки параллельных прямых
Параллельные прямые. Свойства и признаки параллельных прямых Исследование функций и построение графиков
Исследование функций и построение графиков Планиметрия. Обзор методички
Планиметрия. Обзор методички Prezentatsia_2
Prezentatsia_2 Урок математики с элементами театрализации
Урок математики с элементами театрализации Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства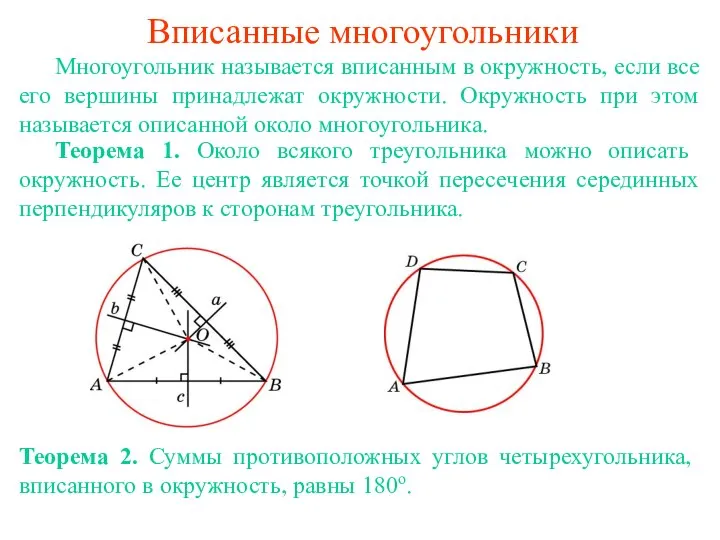 Вписанные и описанные многоугольники
Вписанные и описанные многоугольники множества дистант
множества дистант Домашняя работа. Наурызбай Зарина
Домашняя работа. Наурызбай Зарина Неизвестное делимое
Неизвестное делимое Решение уравнений, содержащих модуль
Решение уравнений, содержащих модуль