Содержание
- 2. Course Title Slide І Математична логіка Ця лекція про: Введення в математичну логіку (продовження) І.4 Рівність
- 3. І.4 Рівність висловлювань Імплікація є найпотрібніша й найцікавіша операція пропозіційної логіки. Імплікація лежить в основі умовних
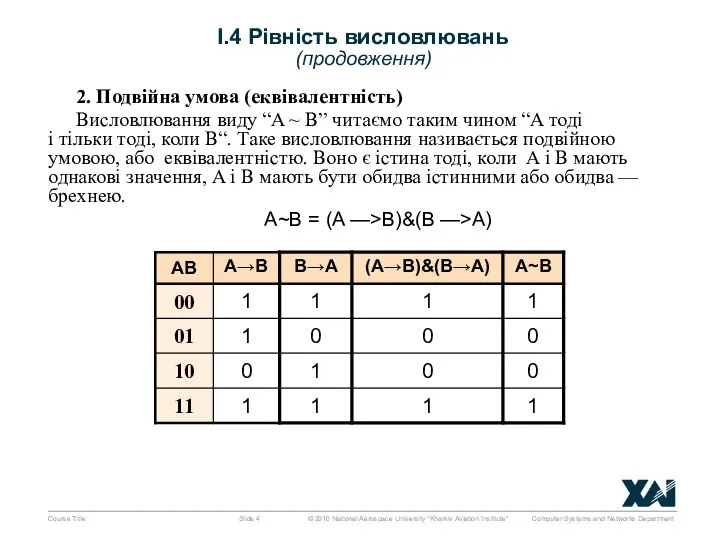
- 4. 2. Подвійна умова (еквівалентність) Висловлювання виду “A ~ B” читаємо таким чином “A тоді і тільки
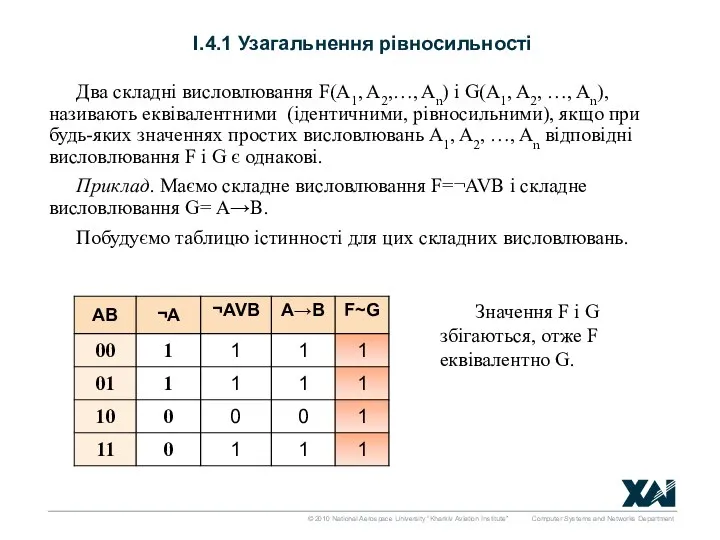
- 5. І.4.1 Узагальнення рівносильності Два складні висловлювання F(A1, A2,…, An) і G(A1, A2, …, An), називають еквівалентними
- 6. Нехай ми маємо вісловлювання А→B, (“Якщо Василь мешкає в Куп’янську (А), тоді Василь мешкає в Харківський
- 7. Course Title Slide Таблиця істинності для закону контрапозиції Значення F і G збігаються при всіх значеннях
- 8. Ми можемо довести еквівалентність двох висловлювань F(A, B) і G(A, B) іншим шляхом (методом міркувань): Для
- 9. Приклади еквівалентностей, які часто використовуються: AVB= ¬(¬AΛ¬B) закон Де Морґана для диз’юнкції; AΛB= ¬(¬AV¬B) закон Де
- 10. І.5 Тавтологія, протиріччя, висловлювання, що виконується, (здійсненне висловлювання) Складне висловлювання називається тавтологією, якщо його значення завжди
- 11. Можливо також довести методом міркувань, що висловлювання є тавтологією (або протиріччям). Доведемо, що F=((A→B) →A) →A
- 12. І.6 Логічний наслідок Складне висловлювання G(A1, A2, …, An) називається логічним наслідком складного висловлювання F(A1, A2,
- 13. Приклад. Маємо висловлювання G=AV(¬B), яке є логічним наслідком висловлювання F=AB V¬A ¬B. Покажемо, що висловлювання H=F→G
- 14. Найвживаніши тавтології A→A Закон визначення. Кожне висловлювання є логічним наслідком самого себе (якщо щось існує, то
- 15. Найвживаніши тавтології (продовження) AΛ (A→B) →B Modus ponens. Правило розподілу. Якщо A є істина, а B
- 16. Course Title Slide Підсумок Отже ви вивчили: Рівність висловлювань; Тавтологію, протиріччя, здійсненне висловлювання; Логічний наслідок; Базові
- 18. Скачать презентацию













 Презентация по математике "Праздник чисел «5 плюс »" -
Презентация по математике "Праздник чисел «5 плюс »" -  Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Старинные меры длины
Старинные меры длины Статистическая проверка гипотез
Статистическая проверка гипотез Сбережение водных ресурсов. Решение задач на сравнение величин
Сбережение водных ресурсов. Решение задач на сравнение величин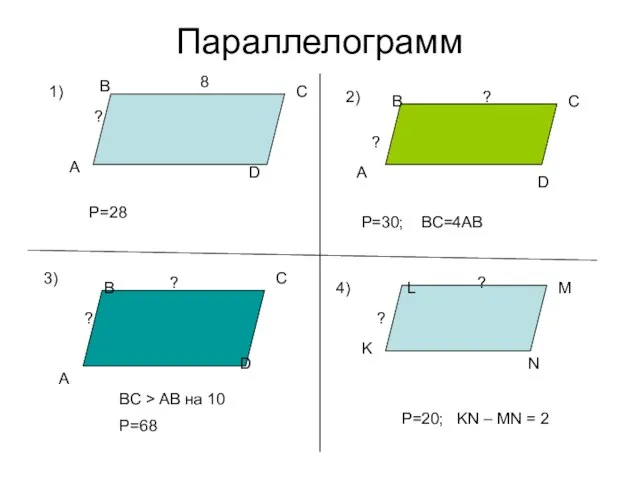 Параллелограмм
Параллелограмм Окружность Аполлония
Окружность Аполлония Формирование и развитие познавательных УУД на уроках математики
Формирование и развитие познавательных УУД на уроках математики Интерактивный плакат Треугольник
Интерактивный плакат Треугольник Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями
Познакомимся с письменным приёмом умножения на числа, оканчивающиеся нулями Тест по теме Окружность
Тест по теме Окружность Презентация на тему Показательная функция: свойства, график
Презентация на тему Показательная функция: свойства, график  Интерактивный пазл
Интерактивный пазл Маршрутный лист группы
Маршрутный лист группы Credit and exam
Credit and exam Квадратные уравнения. Лекция
Квадратные уравнения. Лекция Система быстрого счёта в уме Якова Трахтенберга. Занятия 3
Система быстрого счёта в уме Якова Трахтенберга. Занятия 3 Скалярное произведение векторов
Скалярное произведение векторов Рациональные и действительные числа. Приближенные выражения
Рациональные и действительные числа. Приближенные выражения Планиметрия. Задачи
Планиметрия. Задачи Задача на внимание. 5 класс
Задача на внимание. 5 класс 3.7. Непрерывность функции
3.7. Непрерывность функции Четырехугольники
Четырехугольники Решение задач
Решение задач Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Презентация на тему Функция у=к/х, её свойства и график
Презентация на тему Функция у=к/х, её свойства и график  Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Рисуем по координатам
Рисуем по координатам