Содержание
- 2. ЧТО ТАКОЕ КОМБИНАТОРИКА? Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций,
- 3. Комбинаторика - важный раздел математики, знание которого необходимо представителям самых разных специальностей. С комбинаторными задачами приходится
- 4. « Эн факториал»-n!. Определение. Произведение подряд идущих первых n натуральных чисел обозначают n! и называют «эн
- 5. Комбинации из n-элементов, отличающиеся друг от друга только порядком следования элементов, называются перестановками. Обозначаются Рn Перестановки
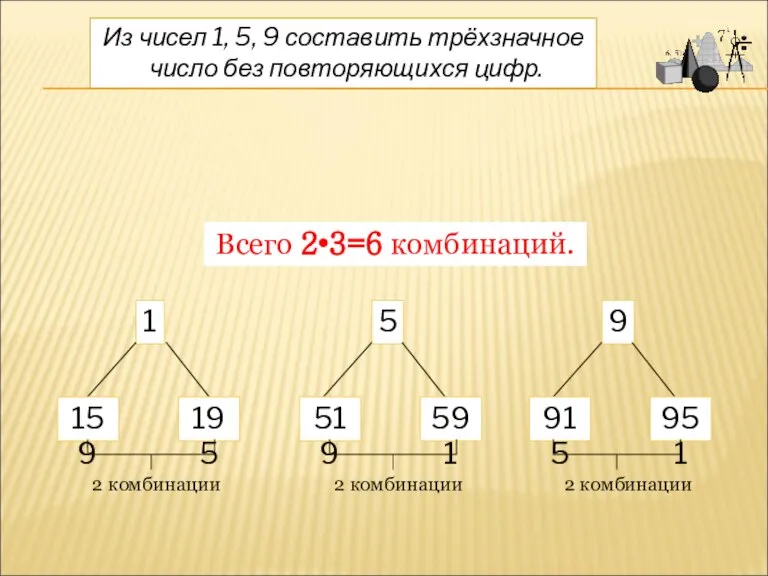
- 6. Из чисел 1, 5, 9 составить трёхзначное число без повторяющихся цифр. 1 159 195 5 9
- 7. Комбинации из n-элементов по k, отличающиеся друг от друга составом и порядком, называются размещениями. Размещения
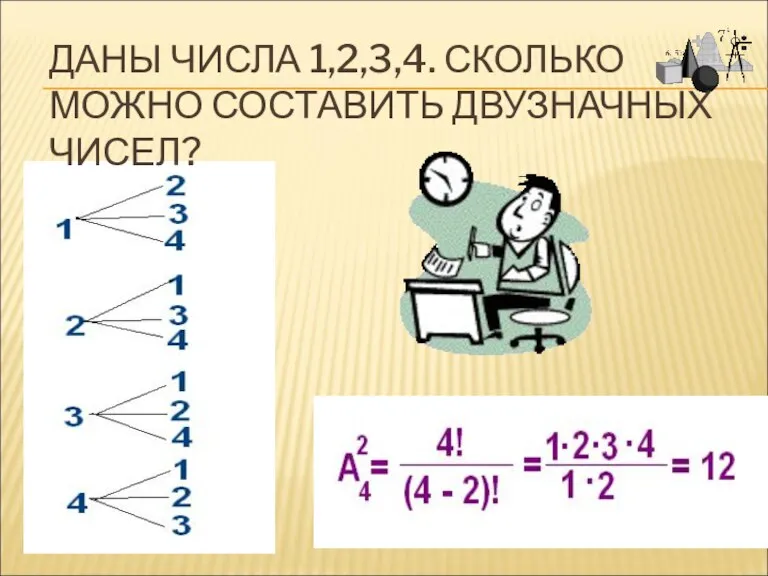
- 8. ДАНЫ ЧИСЛА 1,2,3,4. СКОЛЬКО МОЖНО СОСТАВИТЬ ДВУЗНАЧНЫХ ЧИСЕЛ?
- 9. Комбинации из n-элементов по к, отличающиеся только составом элементов, называются сочетаниями из n -элементов по к.
- 10. РЕШЕНИЕ ЗАДАЧ Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать? Решение: Надо
- 13. Скачать презентацию







 иррациональные_уравнения_2
иррациональные_уравнения_2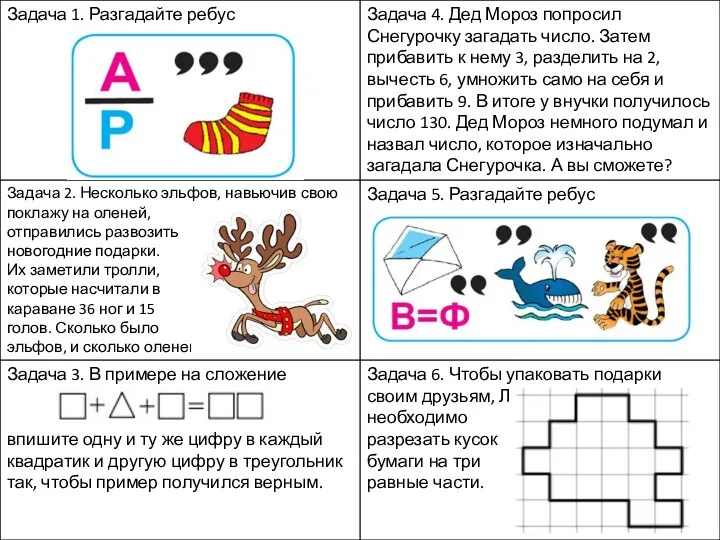 Ребусы по математике
Ребусы по математике Математический диктант №2. Геометрия 7класс. Первый признак равенства треугольников
Математический диктант №2. Геометрия 7класс. Первый признак равенства треугольников Я сдам ЕГЭ. Кинематика
Я сдам ЕГЭ. Кинематика Презентация на тему ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ УРАВНЕНИЙ
Презентация на тему ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ УРАВНЕНИЙ  Числа от 1 до 9. Письмо цифры 9
Числа от 1 до 9. Письмо цифры 9 Характер и ритм линий как средство выражения
Характер и ритм линий как средство выражения Лінійка — найпростіший прилад для вимірювання довжини
Лінійка — найпростіший прилад для вимірювання довжини Таблица единиц времени. 4 класс
Таблица единиц времени. 4 класс Презентация на тему ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ
Презентация на тему ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ  Вычисления и преобразования
Вычисления и преобразования Среднее арифметическое. Урок №2
Среднее арифметическое. Урок №2 Понятие логарифма
Понятие логарифма Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Элементы линейной алгебры и геометрии выпуклых множеств
Элементы линейной алгебры и геометрии выпуклых множеств Логические задачи. 1 класс
Логические задачи. 1 класс Исследование функции на монотонность и экстремум. Построение графиков
Исследование функции на монотонность и экстремум. Построение графиков Застосування криволінійних координат для розв'язування задач
Застосування криволінійних координат для розв'язування задач Векторная алгебра. Расчет модели
Векторная алгебра. Расчет модели Известное и неизвестное
Известное и неизвестное Параллельные прямые в пространстве. Урок геометрии в 10 классе
Параллельные прямые в пространстве. Урок геометрии в 10 классе Предмет, методы и задачи статистики
Предмет, методы и задачи статистики Решение уравнений
Решение уравнений Лекция_04
Лекция_04 ВКР: Исследование динамики итерирования полиномов второй степени и кусочно-линейных функций
ВКР: Исследование динамики итерирования полиномов второй степени и кусочно-линейных функций Треугольник
Треугольник Непрерывные случайные величины
Непрерывные случайные величины Космические тропинки. Урок-игра по математике
Космические тропинки. Урок-игра по математике