Содержание
- 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЁ ГРАФИК
- 3. Функция вида y = kx +b, где k и b числа, а x и y переменные,
- 4. х у 0 k > 0 возрастающая х у 0 k убывающая Свойства линейной функции у
- 5. у = 2 х + 3 х = у = 2 · +3 х 0 =
- 6. Совет: Если коэффициент k положительный, выбирай положительное значение аргумента; если отрицательный - отрицательное
- 7. Через две точки можно провести только одну прямую линию Для построения графика линейной функции достаточно двух
- 8. Коэффициент k называют угловым коэффициентом.
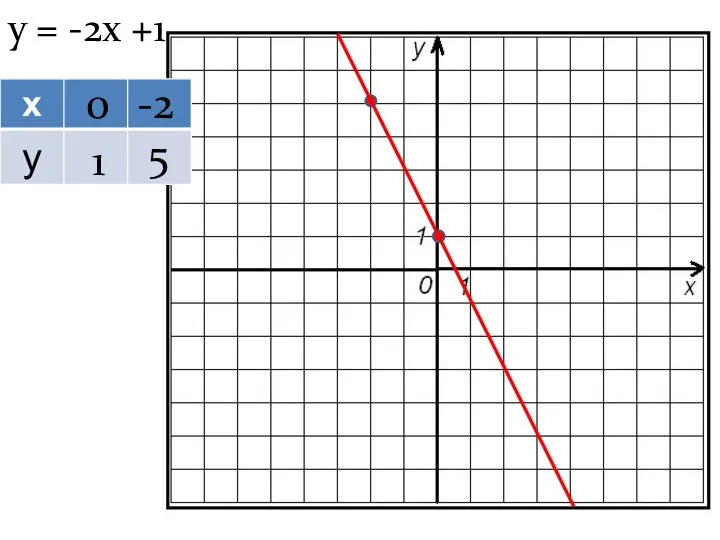
- 9. у = -2х +1 0 -2 1 5
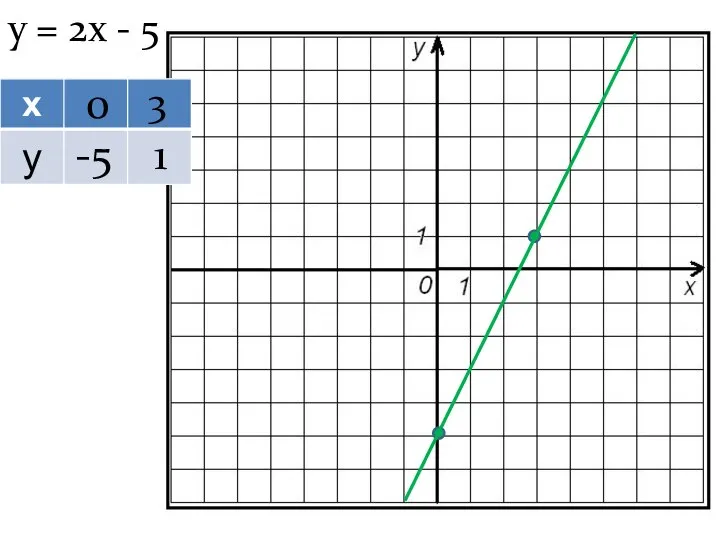
- 10. у = 2х - 5 0 3 -5 1
- 11. Чем больше угловой коэффициент k, тем больше угол, образованный графиком функции с осью ОХ
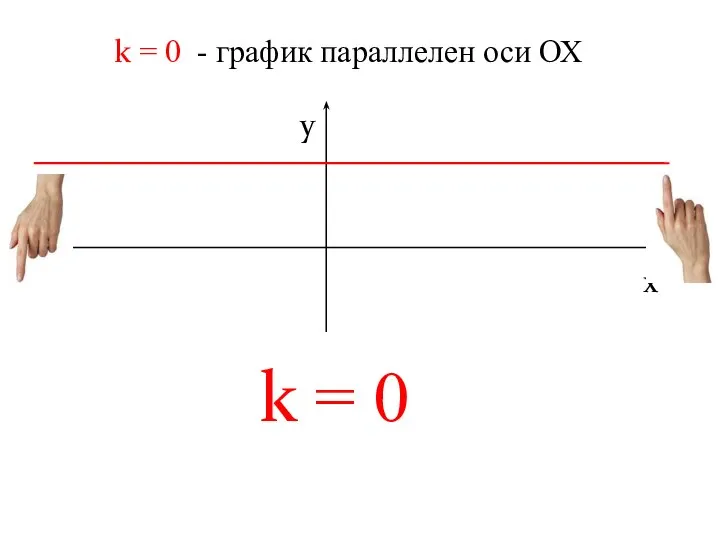
- 12. k = 0 - график параллелен оси ОХ x y k = 0
- 13. Построим несколько графиков линейных функций, у которых одинаковые угловые коэффициенты.
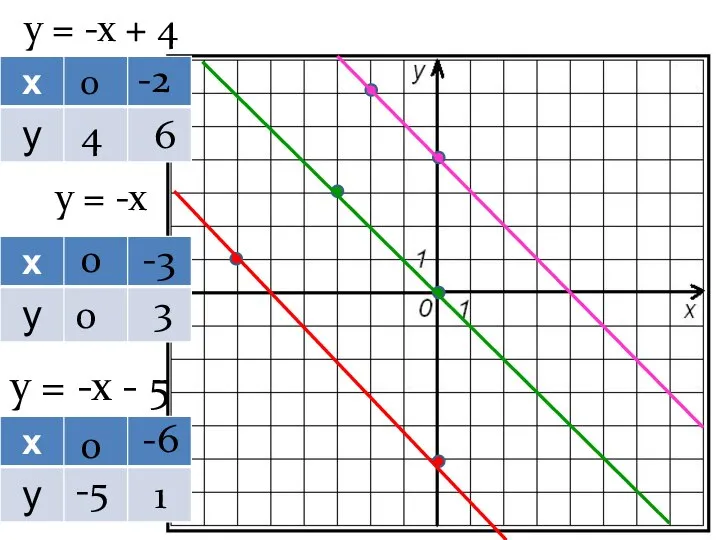
- 14. у = -х + 4 у = -х у = -х - 5 0 4 -2
- 15. Если у линейных функций угловой коэффициент одинаковый, то их графики параллельны!
- 16. Квадратичная функция и ее свойства.
- 17. Определение. Функция вида у = ах2+bх+с, где а, b, c – заданные числа, а≠0, х –
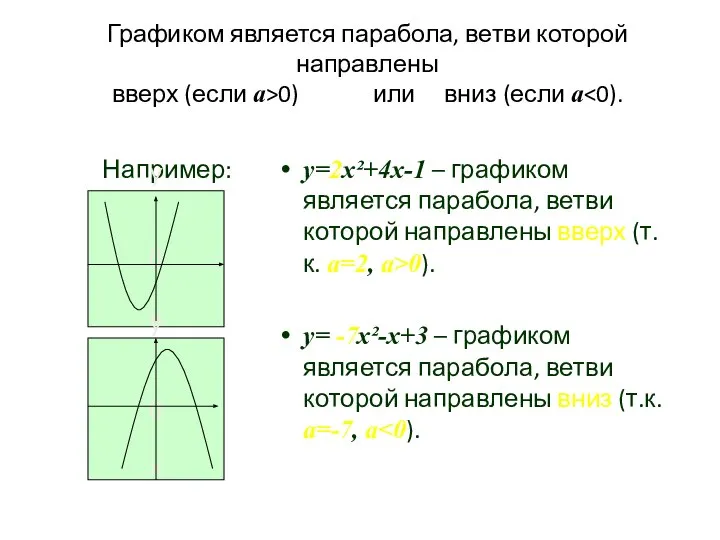
- 18. Графиком является парабола, ветви которой направлены вверх (если а>0) или вниз (если а Например: у=2х²+4х-1 –
- 19. Чтобы построить график функции надо: Описать функцию: название функции, что является графиком функции, куда направлены ветви
- 20. Вершина параболы: Задание. Найти координаты вершины параболы: 1) у = х 2 -4х-5 2) у=-5х 2+3
- 21. Свойства функции у = kx2 1. D (f) = (-∞;+∞) k > 0 k x y
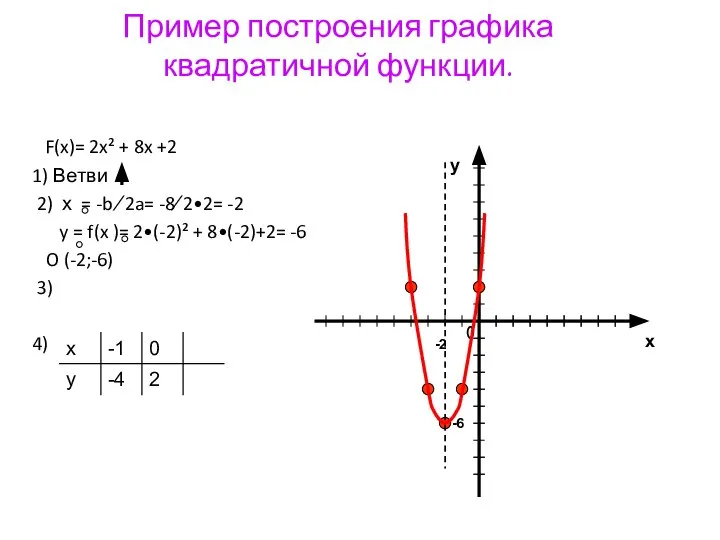
- 22. Пример построения графика квадратичной функции. F(x)= 2x² + 8x +2 1) Ветви 2) х = -b
- 23. Обратная пропорциональность
- 24. Обратной пропорциональностью называется функция, которую можно задать формулой вида где x — независимая переменная у-зависимая переменная
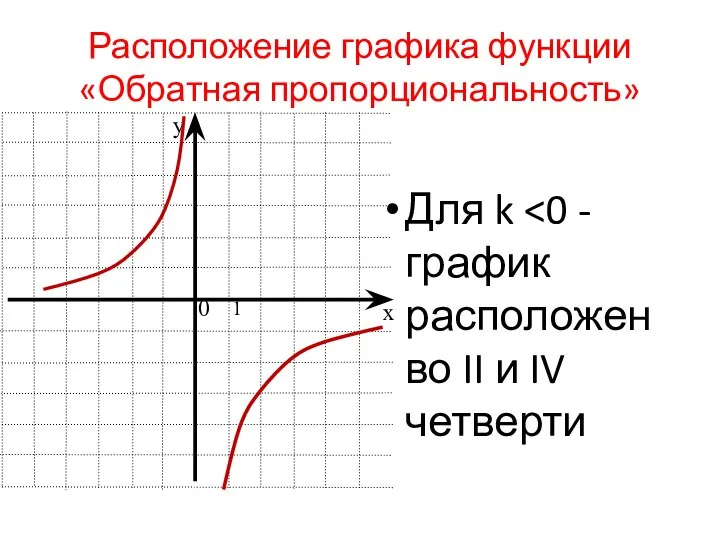
- 25. Расположение графика функции «Обратная пропорциональность» Для k 0 1
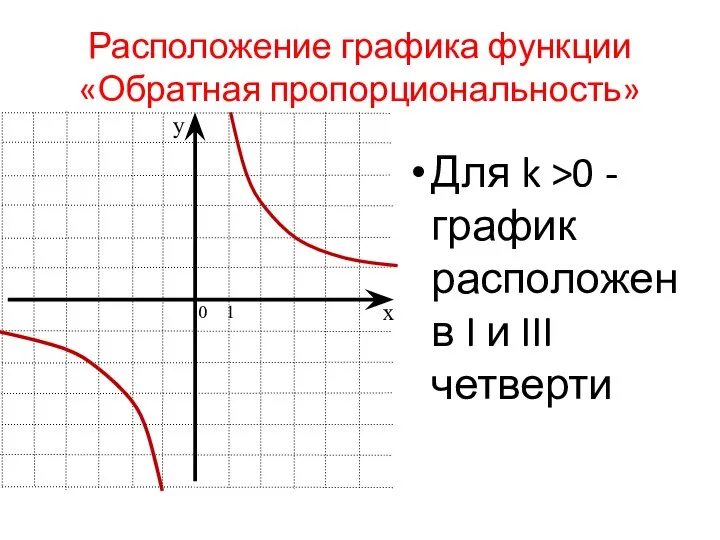
- 26. Расположение графика функции «Обратная пропорциональность» Для k >0 - график расположен в I и III четверти
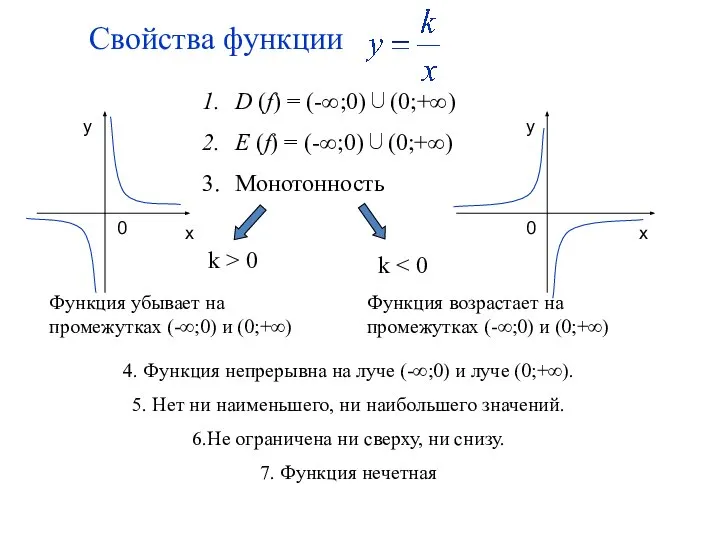
- 27. Свойства функции D (f) = (-∞;0)∪(0;+∞) Е (f) = (-∞;0)∪(0;+∞) Монотонность k > 0 k Функция
- 29. Скачать презентацию



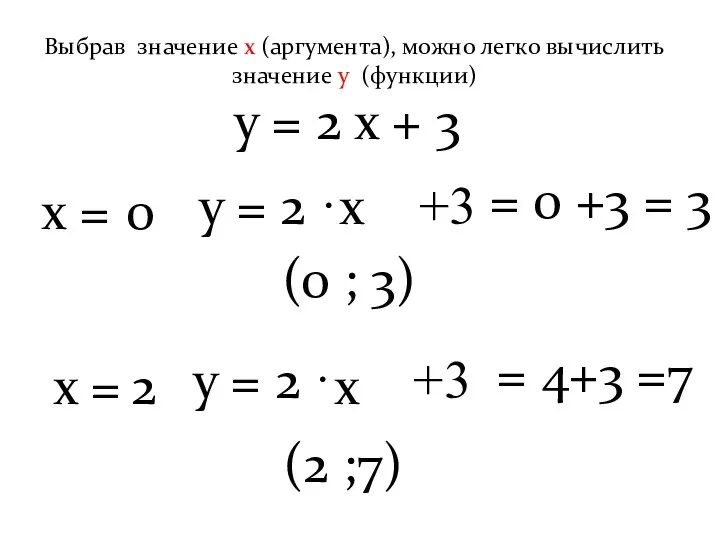












 Системы уравнений. Задание №9. ОГЭ
Системы уравнений. Задание №9. ОГЭ Математические основы экономической кибернетики. Элементы теории множеств и математической логики. (Лекция 1)
Математические основы экономической кибернетики. Элементы теории множеств и математической логики. (Лекция 1) Презентация на тему Наглядная геометрия для начальной школы
Презентация на тему Наглядная геометрия для начальной школы 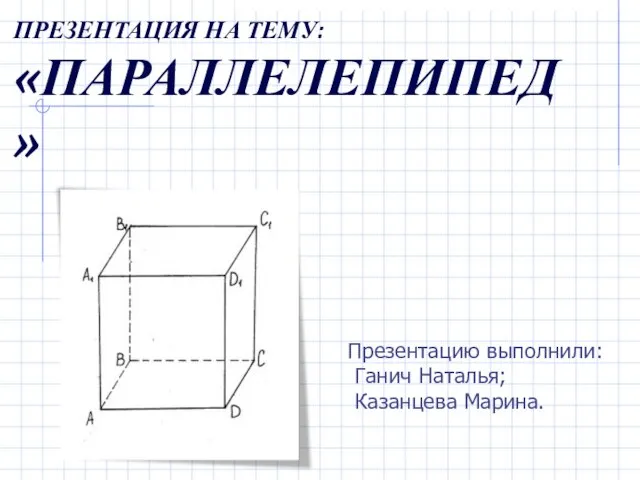 Презентация на тему Параллелепипед (9 класс)
Презентация на тему Параллелепипед (9 класс)  Цветочное настроение (порядковый счет)
Цветочное настроение (порядковый счет) Теорема Муавра -Лапласа
Теорема Муавра -Лапласа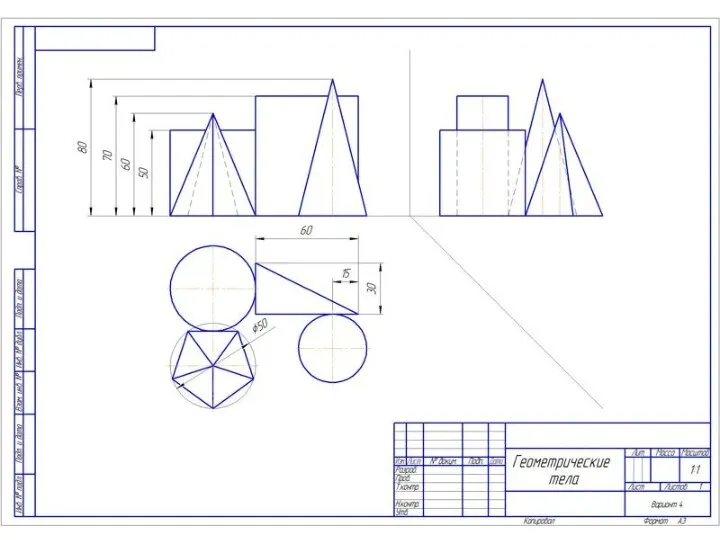 Геометрические тела. 9 класс
Геометрические тела. 9 класс Классические алгоритмы на графах
Классические алгоритмы на графах Движение. Поворот
Движение. Поворот Цилиндр. Конус
Цилиндр. Конус Равносильные формулы. Уроки 17-18
Равносильные формулы. Уроки 17-18 Сокращённая ДНФ
Сокращённая ДНФ Презентация на тему Округление десятичных чисел
Презентация на тему Округление десятичных чисел  Элементы высшей математики
Элементы высшей математики Геометрические иллюзии. Отрезок. Сравнение отрезков. Параллельные прямые
Геометрические иллюзии. Отрезок. Сравнение отрезков. Параллельные прямые Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА
Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА  Элементы математической логики
Элементы математической логики Интерактивная мозаика. Математические тесты
Интерактивная мозаика. Математические тесты Использование циклов
Использование циклов Разбор задачи 3.33 (Катышев, Магнус - Сборник задач по начальному курсу эконометрики)
Разбор задачи 3.33 (Катышев, Магнус - Сборник задач по начальному курсу эконометрики) Функция и график
Функция и график Презентация на тему Умножение
Презентация на тему Умножение  Деление дробей. Растровая графика
Деление дробей. Растровая графика Делимость целых чисел
Делимость целых чисел Презентация по математике "Обзор учебно-методических пособий по новой демоверсии ЕГЭ-2010" -
Презентация по математике "Обзор учебно-методических пособий по новой демоверсии ЕГЭ-2010" -  Линейные уравнения
Линейные уравнения Геометрические фигуры. 1 класс
Геометрические фигуры. 1 класс Определение времени регулирования АС по переходной функции
Определение времени регулирования АС по переходной функции