Слайд 21. Функция
1.1. Некоторые математические символы.
Для краткой записи – кванторы.
1. => - квантор

следования. (α => β – означает: из α следует β)
2. ⬄ - квантор эквивалентности (α эквивалентно β). В формулировке теорем символ соответствует словам «необходимо и достаточно» или «тогда и только тогда».
3. ∀ - квантор общности. Запись (∀х:α) означает: « для любого х справедливо утверждение α.
Слайд 34. ∃ - квантор существования. Запись (∀х:α) означает: существует по крайней мере

один такой Х для которого справедливо предложение α.
1.2. Множества
Множество – первоначальное понятие. A,B,C,…X,Y,Z.
Элементы множества: a,b,c,..x,y,z.
Конечное множество.
Бесконечное множество.
Пустое множество ∅
Слайд 4Элемент принадлежит данному множеству:
α∈А, элемент не принадлежит данному множеству: α∉А.
Пересечение и объединение

множеств.
Вещественные числа.
Целые положительные числа 1,2,3,4… образуют мн-во натуральных чисел. N.
Слайд 5Все числа вида
а также 0 образуют мн-во рациональных чисел: С.
Иррациональные числа: Q
Множество

вещественных чисел:
геометрически изображаются точками на числовой оси. Ось: прямая, указано положительное направление, начало отсчета и отрезок, длина кот. принята за единицу длины.
Слайд 6Абсолютная величина вещественного числа
Модуль.
определяется соотношениями:
-х= x=
x
x<0 x>0
Геометрически:

модуль х – расстояние от точки х до 0
Слайд 7Из определения:
Независимо от взаимного расположения точек – модуль представляет собой расстояние между

ними.
Промежутки. Окрестности.
Открытый интервал – (а,в) или ]a,b[ это множество вещественных чисел, удовл.усл.
Слайд 8Замкнутый интервал: [a,b],
Полуоткрытые интервалы.
Это конечные промежутки.
Бесконечные промежутки:
Множество вещественных чисел R обозначается символом:
Далее:
![Замкнутый интервал: [a,b], Полуоткрытые интервалы. Это конечные промежутки. Бесконечные промежутки: Множество вещественных](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992895/slide-7.jpg)
Слайд 9Окрестность точки: числовое множество
Пусть
По определению:
Геометрически – это отрезок длины
с серединой в точке

а без включения концевых точек. Конечная точка.
а- а а+ R
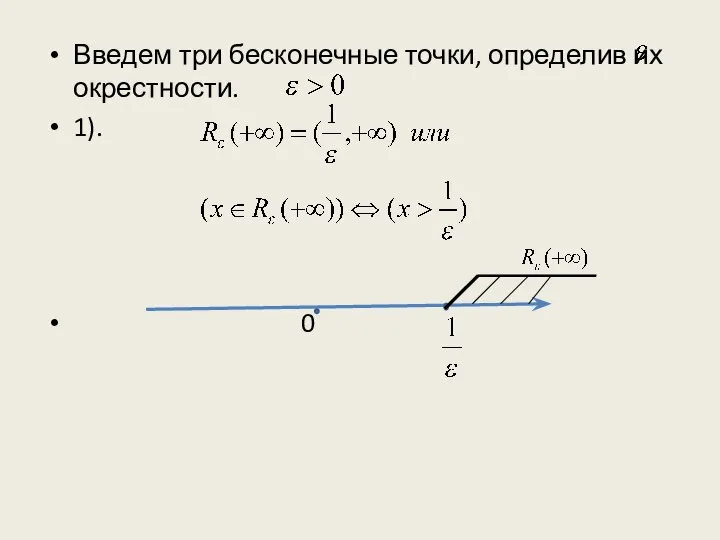
Слайд 10Введем три бесконечные точки, определив их окрестности.
1).
0
Слайд 12Левая и правая окрестности. По определению:
Функция
Определение. Если каждому элементу х∈Х ставится

в соответствие единственный элемент у∈Y, то это соответствие называется функцией (отображением), определённой на множестве Х со значениями в множестве Y. Элемент х называется аргументом, а множество Х – областью определения функции f(х). Элемент у, поставленный в соответствие элементу х называется значением функции f в точке х. Обозначение: у = f(х).
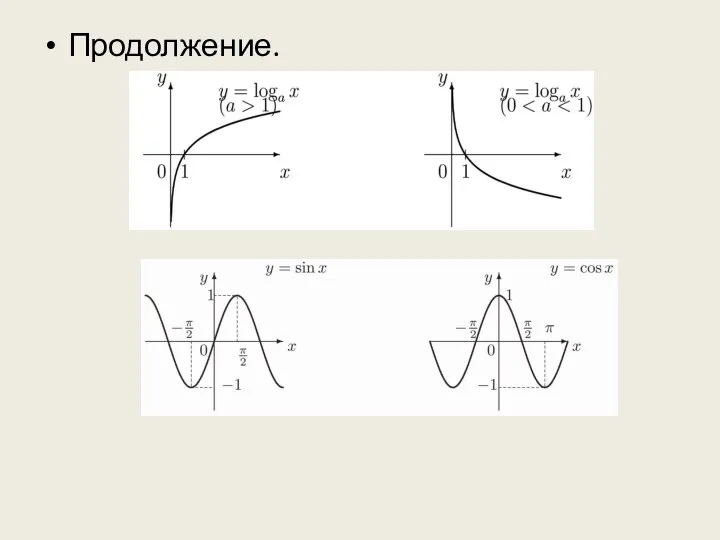
Слайд 13К основным элементарным функции относятся:
степенная функция y = xα, α ∈

R, α ≠0;
показательная функция у =ах, а > 0, а ≠ 1;
логарифмическая функция у = logах, а > 0, а ≠ 1;
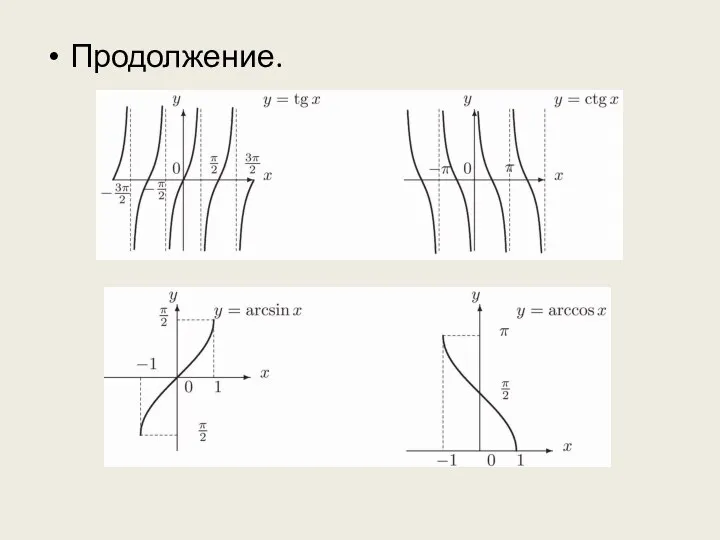
тригонометрические функции y = sinx, y = cosx, y = tgx, y = ctgx;
Слайд 14обратные тригонометрические функции y = arcsinx, y = arccosx, y = arctgx, y =

arcctgx.
Слайд 17arctgx, arcctgx:
Если у = f(и), и = ϕ(x), то функция y =

f(φ(x)) называется сложной функцией (функцией от функции, суперпозицией функций) аргумента х; аргумент u функции f называется промежуточным. Например, если и U=sinx
то суперпозицией этих функций является .
Слайд 18Свойства функций.
Функция называется чётной, если f(–x) = f (x), и нечётной, если

f (–x) = – f (x). Например, x, x3, 1/x, sinx, tgx, ctgx, arcsinx, arctgx (cм.рис.) – нечётные функции, а x2, cosx – чётные функции.
Функция f(x) называется возрастающей на Х, если большему значению аргумента соответствует большее значение функции, т.е.
∀х1, х2 ∈Х, х1 < х2 ⇒ f(x1) < f(x2),
и убывающей на Х, если
∀х1, х2 ∈Х, х1 < х2 ⇒ f(x1) > f(x2).
Слайд 19Если неравенства нестрогие, то функции называются соответственно неубывающей и невозрастающей. Возрастающие, убывающие,

невозрастающие и неубывающие на Х функции называются монотонными. Например, ах, logах (см. рис.) – монотонные функции, возрастающие при а > 1 и убывающие при 0 < а < 1.
Функция f(x) называется ограниченной на Х, если существует число М > 0, при котором выполняется
< М для ∀х∈Х. Например, sinx, cosx (см. рис.), arcsinx, arccosx, arctgx, arcctgx – ограниченные функции.
Слайд 20Функция f(x) называется периодической, если существует Т > 0, при котором выполняется f(х + Т) = f(x) для

всех х ∈ R. Т – период функции, число nТ также является ее периодом.
Рациональные и дробно-рациональные функции
Целая рациональная функция (многочлен, полином) имеет вид
n ∈ N.
Если a является корнем многочлена, то






![Замкнутый интервал: [a,b], Полуоткрытые интервалы. Это конечные промежутки. Бесконечные промежутки: Множество вещественных](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992895/slide-7.jpg)


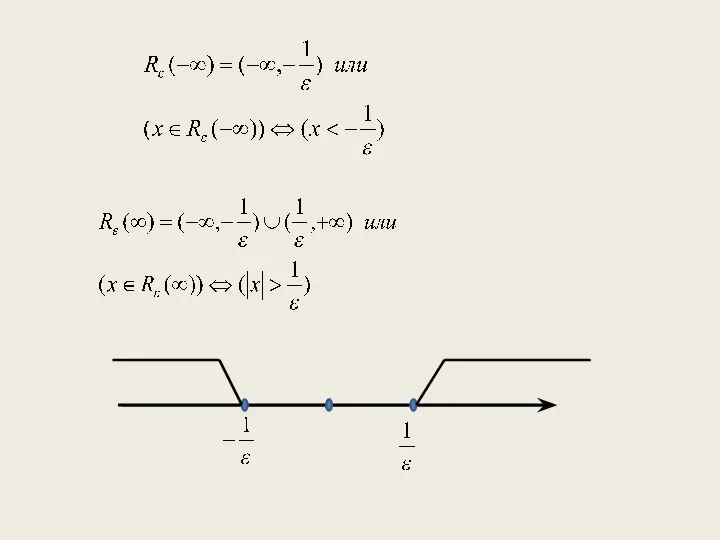







 Угол между прямыми
Угол между прямыми Неопределённый интеграл
Неопределённый интеграл Вычисление площадей и объемов. Лекция 5
Вычисление площадей и объемов. Лекция 5 Прямоугольный параллелепипед
Прямоугольный параллелепипед Построение цилиндра в изометрической проекции
Построение цилиндра в изометрической проекции Построение графика функции
Построение графика функции Ряд Тейлора функции многих переменных. Лекция 19
Ряд Тейлора функции многих переменных. Лекция 19 Презентация на тему Решение задач В10 (ЕГЭ 2012)
Презентация на тему Решение задач В10 (ЕГЭ 2012)  Преобразование рациональных выражений
Преобразование рациональных выражений Биматричные игры
Биматричные игры Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Математическая игра Счастливое число 7!
Математическая игра Счастливое число 7!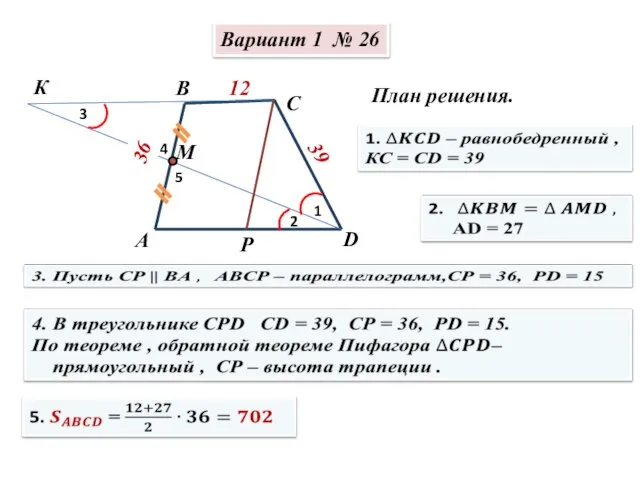 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Сравнение множеств. Отображения множеств
Сравнение множеств. Отображения множеств Луч. Отрезок. Путешествие точки
Луч. Отрезок. Путешествие точки Презентация на тему Биссектриса угла в треугольнике
Презентация на тему Биссектриса угла в треугольнике  08_ ОТС_ Основы теории СП-2
08_ ОТС_ Основы теории СП-2 Сложение и вычитание многочленов
Сложение и вычитание многочленов Чётность и нечётность, периодичность тригонометрических функций с изменениями
Чётность и нечётность, периодичность тригонометрических функций с изменениями Случаи вычитания 17 -
Случаи вычитания 17 - Интерактивный тест Степень. Свойства степени
Интерактивный тест Степень. Свойства степени Модели пирамид
Модели пирамид Математика задача. Решение задачи уч. Стр.92 №2
Математика задача. Решение задачи уч. Стр.92 №2 Математика в профессии повара
Математика в профессии повара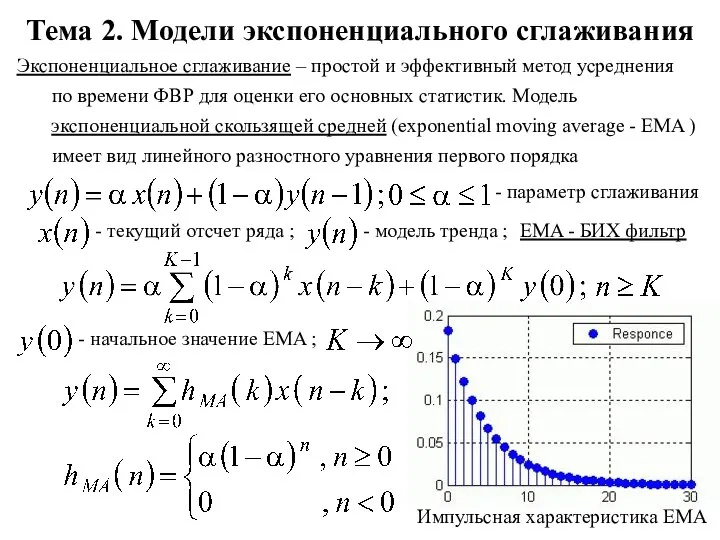 Модели экспоненциального сглаживания. Тема 2
Модели экспоненциального сглаживания. Тема 2 Презентация на тему Касательная к графику функции
Презентация на тему Касательная к графику функции  Треугольник. Виды треугольников
Треугольник. Виды треугольников