в стоячей воде. Сколько процентов скорости лодки в стоячей воде составляет скорость течения?
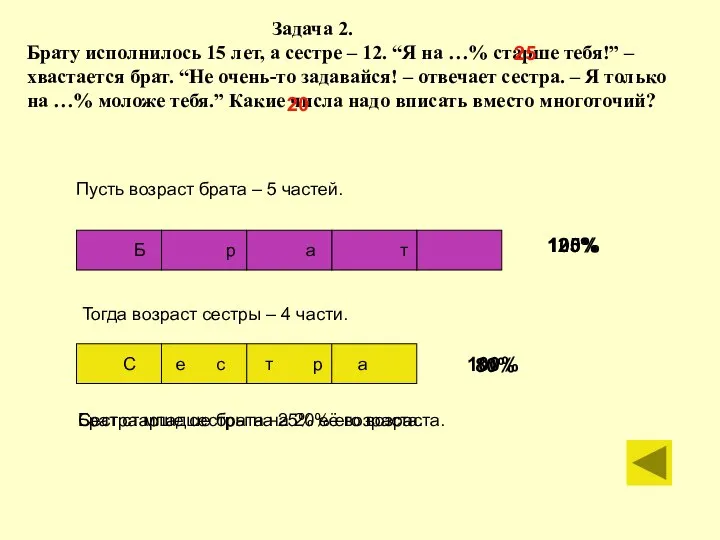
2. Брату исполнилось 15 лет, а сестре – 12. “Я на …% старше тебя!”
– хвастается брат. “Не очень-то задавайся! – отвечает сестра.
– Я только на …% моложе тебя.” Какие числа надо вписать
вместо многоточий?
3. Несла Варя ведро воды из колодца. Видит, ребятишки на санках
катаются. Оставила ношу и – к ним. Накаталась вдоволь, вспомнила
ведре, а оно лопнуло, и лед в нем вместо воды. Дома дед объяснил:
“Вода замерзшая увеличивается в объеме на 10%.” Стала Варя соображать:
“На сколько процентов уменьшается объем льда при таянии?”
Посчитайте и вы.
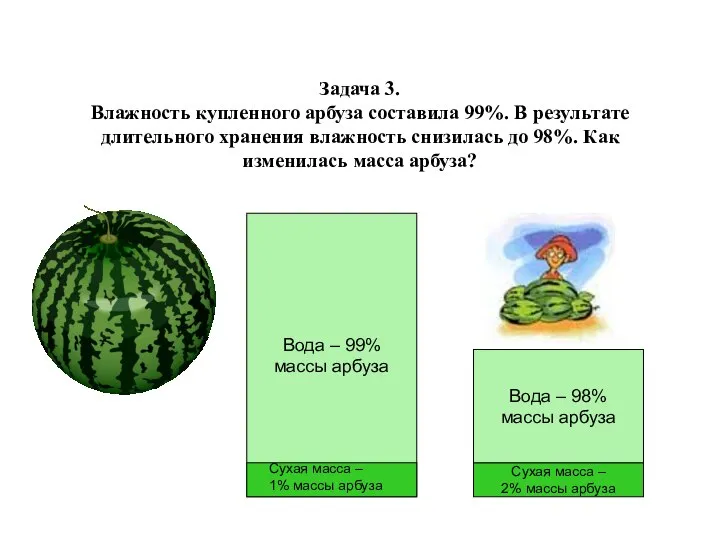
4. Свежие грибы содержат 98% воды и весят 100 кг. При хранении они
усохли и воды оказалось 96%. Найдите массу грибов после высыхания.
Решение
Решение
Решение
Решение
5. В траве содержится 60% воды, а в сене 20% воды. Сколько сена
получится из тонны травы?
Решение
6. Товар подешевел на 20%. На сколько процентов больше можно купить
товара за те же деньги?
Решение










 Решение заданий ЕГЭ уровня С2 (1 часть)
Решение заданий ЕГЭ уровня С2 (1 часть) Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Признаки делимости на 2, 5,10, 3, 6 и 9
Признаки делимости на 2, 5,10, 3, 6 и 9 Параллельные прямые в пространстве
Параллельные прямые в пространстве Неопределенный интеграл
Неопределенный интеграл Урок 53. Расстояние от точки до прямой
Урок 53. Расстояние от точки до прямой Степень с рациональным показателем
Степень с рациональным показателем Косинус угла
Косинус угла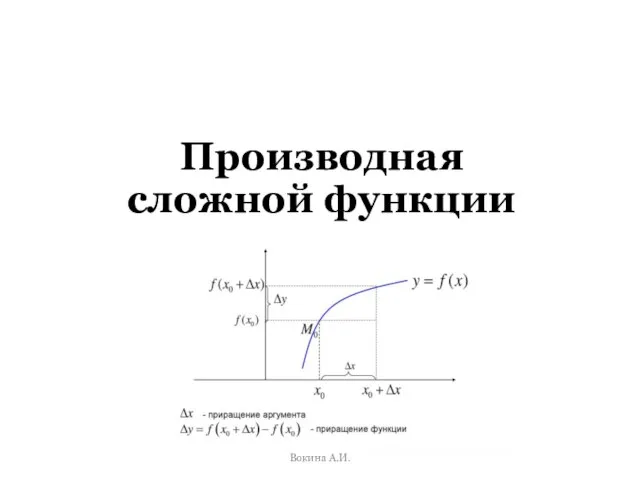 Производная сложной функции
Производная сложной функции Понятие вектора
Понятие вектора Определители. Матрица и ее определитель
Определители. Матрица и ее определитель Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Задания на развитие логики
Задания на развитие логики 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций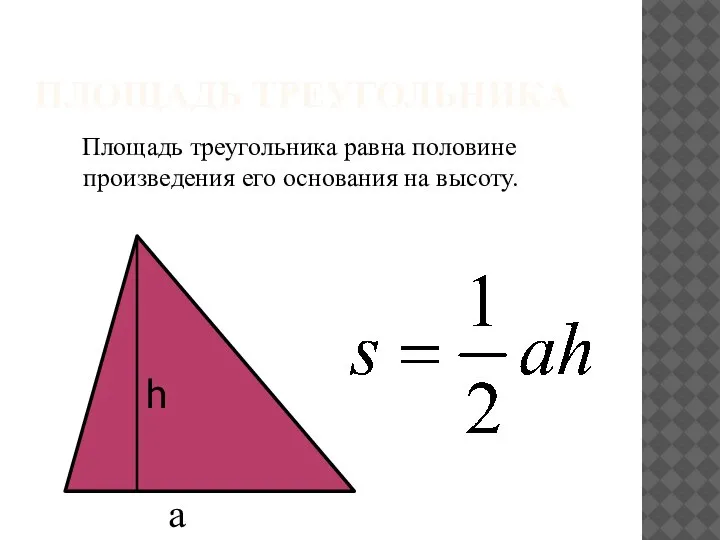 Площадь треугольника
Площадь треугольника Математика без границ. Конкурс
Математика без границ. Конкурс Сантиметр. Линейка
Сантиметр. Линейка Золотое сечение
Золотое сечение Информатика. Вероятность
Информатика. Вероятность Загадки и тайны треугольника
Загадки и тайны треугольника Сложение вида + 2, + 3
Сложение вида + 2, + 3 Презентация на тему Признаки равенства треугольников
Презентация на тему Признаки равенства треугольников  Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Умножение одночлена на многочлен
Умножение одночлена на многочлен Современная финансовая математика
Современная финансовая математика Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Плоскость и прямая в пространстве
Плоскость и прямая в пространстве