Слайд 21. Основные понятия теории статистических гипотез
Статистическая гипотеза – это любое предположение о

виде неизвестного распределения или о параметрах известных распределений.
Статистическая гипотеза – это всякое высказывание о генеральной совокупности, проверяемое по выборке.
Слайд 3Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез.

Слайд 4Гипотезы будем обозначать буквой Н с индексами. Будем предполагать, что у нас

имеется 2 непересекающиеся гипотезы H0 и H1.
H0 – нулевая гипотеза (или основная).
H1 – альтернативная или конкурирующая гипотеза.
Слайд 5Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки.
Задача

проверки статистических гипотез состоит в том, чтоб на основе выборки
принять (т. е. считать справедливой) либо нулевую гипотезу , либо конкурирующую гипотезу .
Слайд 6При проверке гипотезы может быть принято неправильное решение, то есть могут быть

допущены ошибки двух родов:
Ошибка первого рода состоит в том, что отвергается нулевая гипотеза H0, когда на самом деле она верна.
Ошибка второго рода состоит в том, что отвергается альтернативная гипотеза H1, когда на самом деле она верна.
Слайд 7Рассматриваемые случаи наглядно иллюстрирует следующая таблица.
Вероятность ошибки первого рода называется уровнем значимости
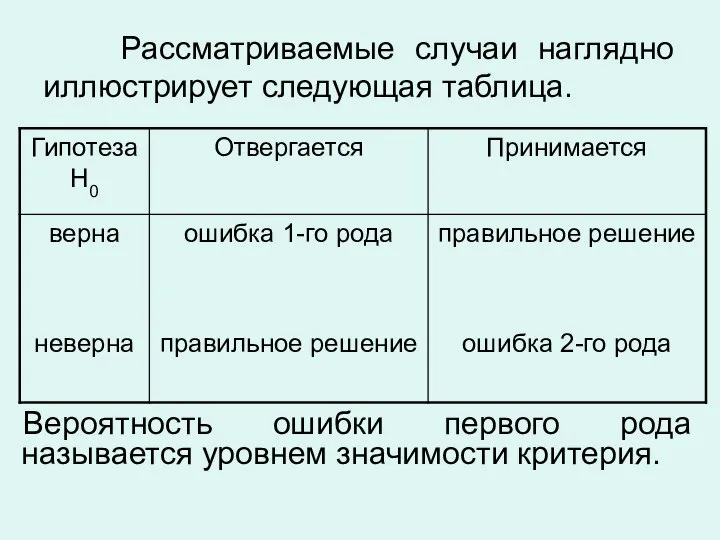
критерия.
Слайд 8Для проверки принятой гипотезы используют статистический критерий – это правило, позволяющее, основываясь

только на выборке , принять либо отвергнуть нулевую гипотезу .
Различают два вида критериев: параметрические и непараметрические.
Слайд 9Параметрические критерии представляют собой функции параметров данной совокупности и используются, если совокупности,

из которых взяты выборки, подчиняются нормальному закону распределения.
Непараметрические критерии применяются, если нет подчинения распределения нормальному закону.
Слайд 102. Общая постановка задачи проверки гипотез
1. Формулируют (выдвигают) нулевую гипотезу об

отсутствии различий между группами, об отсутствии существенного отличия фактического распределения от некоторого заданного, например, нормального, экспоненциального и др.
Слайд 11Сущность нулевой гипотезы : разница между сравниваемыми генеральными параметрами равна нулю, и

различия, наблюдаемые между выборочными характеристиками, носят случайный характер, то есть эти выборки принадлежат одной генеральной совокупности.
Слайд 122. Формулируют противоположную нулевой альтернативную гипотезу .
3. Задают уровень значимости .
Уровень

значимости - это вероятность ошибки отвергнуть нулевую гипотезу , если на самом деле эта гипотеза верна.
При ошибка возможна в 5% случаев.
Слайд 134. Для проверки выдвинутой гипотезы используют критерии.
Критерий – это случайная величина К,

которая служит для проверки H0. Эти функции распределения известны и табулированы.
Критерий зависит от двух параметров: от числа степеней свободы и от уровня значимости. Фактическую величину критерия получают по данным наблюдения .
Слайд 145. По таблице определяют критическое значение, превышение которого при справедливости гипотезы маловероятно

6. Сравнивают и .
Если , то отвергают H0 и принимают H1.
Если , то отвергают H1 и принимают H0.
7. Вывод: различие статистически значимо (0,05) или незначимо .
Слайд 153. Проверка гипотез относительно средних
Сравнивают друг с другом две независимые выборки

объемов n1 и n2 , взятые из нормально распределенных совокупностей с параметрами M(X1) и M(X2) . Дополнительно предполагаем, что неизвестные генеральные дисперсии равны между собой. По этим выборкам найдены соответствующие выборочные средние и
и исправленные дисперсии S12 и S22. Уровень значимости задан.
Слайд 161. Нулевая гипотеза H0: M(X1) = M(X2) ;
2. Альтернативная гипотеза H1:
3.

4. Для проверки нулевой гипотезы в этом случае можно использовать критерий Стьюдента сравнения средних.
Величину критерия находим по формуле:
Слайд 17Доказано, что величина при справедливости нулевой гипотезы имеет
t – распределение Стьюдента

с
степенями свободы.
Слайд 185. По таблице находим
6. Сравниваем tКРИТ и tНАБЛ .
Если
Если различие

достоверно
Слайд 19Пример.
По двум независимым малым выборкам объемов n1=5 и n2=6 , извлеченным

из нормальных генеральных совокупностей X1 и X2, вычислены выборочные средние:
и .
Известно, что генеральные дисперсии примерно равны, т. е. .
При уровне значимости проверить нулевую гипотезу H0: M(X1) = M(X2) если
.
Слайд 20Решение.
Вывод: выборочные средние различаются значимо .

Слайд 214. Проверка гипотез о законах распределения
Во многих практических задачах закон распределения

случайных величин заранее не известен, и надо выбрать модель, согласующуюся с результатами наблюдений.
Выдвигают нулевую гипотезу: неизвестная функция распределения исследуемой случайной величины X распределена по некоторому теоретическому закону, например, по нормальному закону
Слайд 22В качестве этой теоретической модели может быть рассмотрен любой закон, например, экспоненциальный

или биномиальное распределение.
Это определяется сущностью изучаемого явления, а также результатами предварительной обработки наблюдений: формой графика распределения, соотношениями между выборочными данными.
Слайд 23Выдвигается альтернативная гипотеза, что данная генеральная совокупность не распределена по закону :
Задается

уровень значимости, например,
Если хотим проверить, согласуются эмпирические данные с нашим гипотетическим предположением относительно теоретической функции распределения или нет, то используем критерий согласия.
Слайд 24Критерий согласия – это критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Рассмотрим

один из них, использующий распределение и получивший название критерий согласия Пирсона.
Применим критерий к проверке нулевой гипотезы , что генеральная совокупность распределена нормально.
Слайд 25Критерий предполагает, что результаты наблюдений сгруппированы в вариационный ряд и разбиты на

классы.
По выборке объема n построим эмпирическое распределение :
варианты: ;
эмпирические частоты: ;
и сравним его с предполагаемым теоретическим распределением, вычисленным в предположении нормального закона распределения.
Теоретические частоты: .
Слайд 26То есть фактически
В качестве критерия проверки нулевой гипотезы примем случайную величину:

,
где k – число классов.
Из таблиц находим .
Сравниваем, если
- расхождение теоретических и эмпирических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном законе распределения генеральной совокупности.
Слайд 27Пример.
При уровне значимости проверить гипотезу о нормальном распределении генеральной совокупности, если известны

эмпирические и теоретические частоты.
эмпирические частоты: 6 13 38 74 106 85 30 14;
теоретические частоты: 3 14 42 82 99 76 37 13.


























 Презентация на тему Сечения многогранников
Презентация на тему Сечения многогранников  Заколдованные цифры
Заколдованные цифры Объёмные и плоские геометрические фигуры
Объёмные и плоские геометрические фигуры Случаи сложения вида +7
Случаи сложения вида +7 Матрица размера m x n
Матрица размера m x n Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ
Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ Собирательные числительные
Собирательные числительные Решение задач с помощью составления систем уравнений
Решение задач с помощью составления систем уравнений Параллелограмм
Параллелограмм Системы линейных уравнений
Системы линейных уравнений Устный счёт
Устный счёт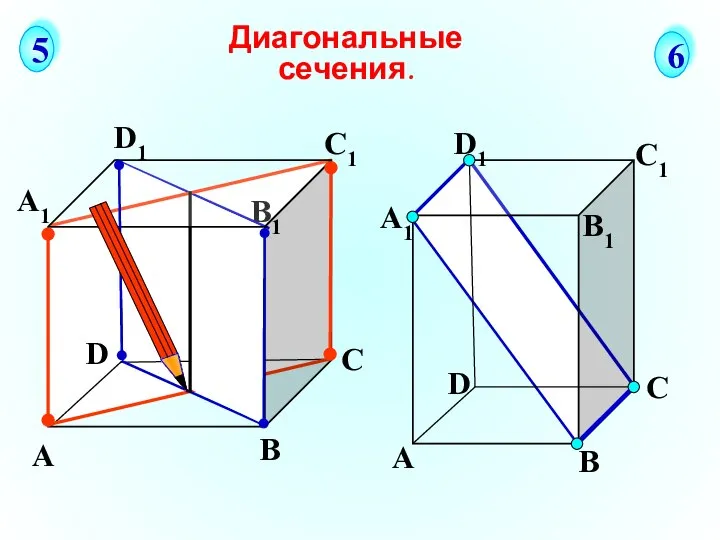 Диагональные сечения
Диагональные сечения Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Метод координат
Метод координат Нахождение площади и периметра прямоугольника. Применение формул на практике
Нахождение площади и периметра прямоугольника. Применение формул на практике Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности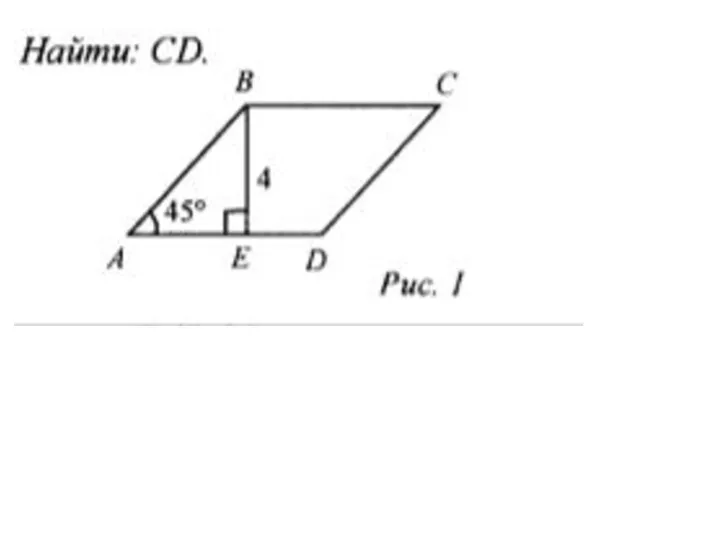 Вычисление площадей
Вычисление площадей Производная сложной функции
Производная сложной функции Обучающие слайды
Обучающие слайды Задача на процкеты
Задача на процкеты Презентация на тему Симметрия и движение (9 класс)
Презентация на тему Симметрия и движение (9 класс)  Составление систем уравнений Колмогорова. Математическое моделирование
Составление систем уравнений Колмогорова. Математическое моделирование Математический диктант по теме: Дроби. 6 класс
Математический диктант по теме: Дроби. 6 класс Дробная схватка
Дробная схватка Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Математика и здоровье. Математика и медицина
Математика и здоровье. Математика и медицина Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Презентация на тему Центральные углы и углы, вписанные в окружность
Презентация на тему Центральные углы и углы, вписанные в окружность