Содержание
- 2. №1«Понятие вектора. Равенство векторов». Скалярные величины определяются заданием своих числовых величин, то есть не имеют направление
- 3. #3)Какие векторы называются коллинеарными? Приведите пример сонаправленных и противоположных направленных векторов. Рис.3 Рис.2 #4)Какие векторы называются
- 4. #5)Какая связь между равенством векторов и параллельным переносом? Теорема. Равные векторы можно совместить параллельным переносом, и
- 5. #7)Что вы знаете о нулевом векторе? #6)Что такое (модуль) длина вектора?
- 6. «№2.Сложение и вычитание векторов». #1)Сформулируйте правило треугольника и правило параллелограмма сложения векторов. Рис.6. A B C
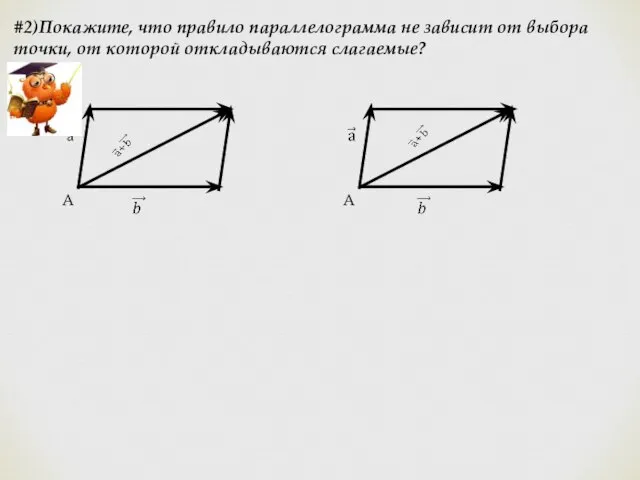
- 7. #2)Покажите, что правило параллелограмма не зависит от выбора точки, от которой откладываются слагаемые? A A
- 8. #3)Какими свойствами обладает сумма векторов? 1) Сложение векторов подчиняется закону ассоциативности, т.е. верно равенство. 2) Существует
- 9. #6)Какие можно разложить вектор на сумму составляющих по двум пересекающимся прямым? Рис.10. Рис.11. O O a
- 10. «№3.Умножение вектора на число и его свойства». #2)Как умножить ненулевое число на ненулевой вектор?
- 11. #3)Какими свойствами обладает умножение числа на вектор?
- 12. #4)Докажите признаки коллинеарности векторов. #5)Какое условие является необходимым и достаточно для того, чтобы точки A,B и
- 13. «№4.Угол между векторами. Скалярное произведение векторов». O O2 O1 O A1 B1 A B Рис.12 Рис.13
- 14. #3)Что называется скалярным произведением двух векторов? Скалярное произведение векторов является числом или вектором? Результат скалярного произведения
- 15. #4)Сформулируйте свойства скалярного произведения.
- 16. #5)Какое условие является необходимым и достаточным для перпендикулярности двух векторов?
- 17. «№5.Координаты вектора». #1)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам. Рис.14. O A
- 18. #2)Какие векторы называются базисными векторами на плоскости? Из теоремы о разложении вектора по двум неколлинеарным векторам
- 19. #5)Какие свойства координат векторов вы знаете? Докажите их.
- 20. #7)Как определяются координаты вектора, если заданы координаты его концов? #6)Какой вектор называется радиус-вектором точки А? #8)По
- 21. #2)Напишите условие перпендикулярности векторов и докажите его. #3)По какой формуле определяется угол между векторами? Докажите её.
- 22. «№7.Различные способы задания прямой в прямоугольной системе координат». #1)Какой вектор называется направляющим вектором прямой? Определение: Направляющий
- 23. #2)Какая точка называется начальной точкой прямой? Напишите уравнения прямой по точке и направляющему вектору. Каков смысл
- 24. #3)Напишите уравнения прямой, проходящей через две заданные точки:С(2;5) и D(5;2). Решение: Уравнение прямой которая проходит через
- 25. #5)Напишите по общему уравнения прямой направляющий вектор, вектор нормали и угловой коэффициент этой прямой.
- 26. #6)По какой формуле определяется угол между прямыми? По формуле: #7)Как определяется расстояние от точки до прямой?
- 28. Скачать презентацию
























 Комбинаторная задача с монетами
Комбинаторная задача с монетами Тестовые задания
Тестовые задания Производная и ее применение
Производная и ее применение Окружность и круг
Окружность и круг Математическая статистика
Математическая статистика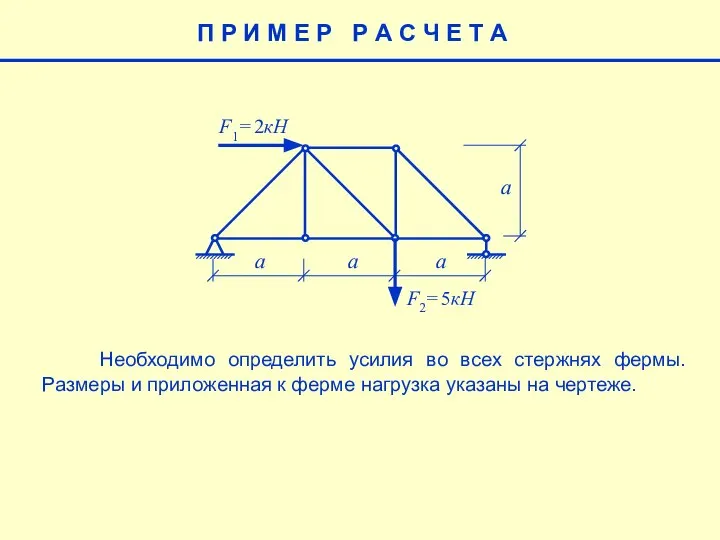 Методы расчета ферм
Методы расчета ферм Презентация на тему Золотое сечение-гармония математики
Презентация на тему Золотое сечение-гармония математики  Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Тела вращения. Урок 142
Тела вращения. Урок 142 Элементы теории вероятностей
Элементы теории вероятностей математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Деление дробей. Решение задач
Деление дробей. Решение задач Линейные алгоритмы
Линейные алгоритмы Круговая окружность
Круговая окружность Эйлеровы и гамильтоновы графы
Эйлеровы и гамильтоновы графы Возрастание и убывание функции
Возрастание и убывание функции Таблица Шульте
Таблица Шульте Планиметрия малыми порциями
Планиметрия малыми порциями Вычитание (Помоги Буратино исправить ошибки)
Вычитание (Помоги Буратино исправить ошибки)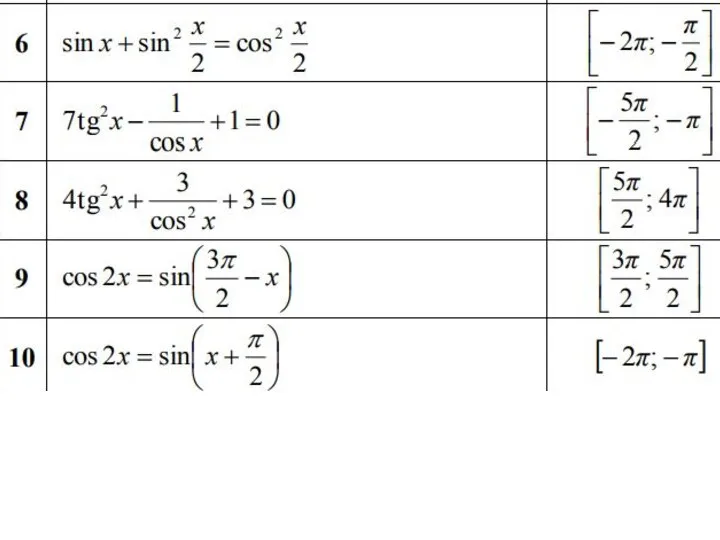 Решение уравнений
Решение уравнений 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Методы статистического анализа литературных текстов
Методы статистического анализа литературных текстов Прямоугольные треугольники
Прямоугольные треугольники Элективный курс. Алгебра 11 класс. Уроки 07-08
Элективный курс. Алгебра 11 класс. Уроки 07-08 Практикум №5 (вторая часть РГР). Построение эконометрических моделей нелинейной парной регрессии (НПР)
Практикум №5 (вторая часть РГР). Построение эконометрических моделей нелинейной парной регрессии (НПР) Натуральный ряд чисел
Натуральный ряд чисел Многогранный угол. Трёхгранный угол
Многогранный угол. Трёхгранный угол