Содержание
- 2. Это утверждение непосредственно следует из определения 6 и теоремы 2.3.
- 3. Примеры. Таким образом, циклическая группа, порождённая матрицей А, имеет порядок 2. Таким образом, теперь подгруппа, порождённая
- 4. 8. –
- 6. (1) Разделим с остатком k на n: k = nt + r, 0 ≤ r
- 7. Доказательство. Разделим с остатком k на n: k = nt + r, 0 ≤ r
- 8. Примеры. В качестве порождающего элемента можно выбрать число 1 или число –1. Других порождающих элементов у
- 9. Доказательство. (2) следует из (1) и из утверждения (2) теоремы 3.1. Пример. Z6 ={0, 1, 2,
- 10. Теорема 3.4. (о подгруппах циклической группы) (1) Любая подгруппа циклической группы сама является циклической. (2) Имеется
- 11. Таким образом, имеем инъекцию из множества делителей порядка группы G в множество её циклических подгрупп. Следовательно,
- 13. Скачать презентацию










 Прямоугольник
Прямоугольник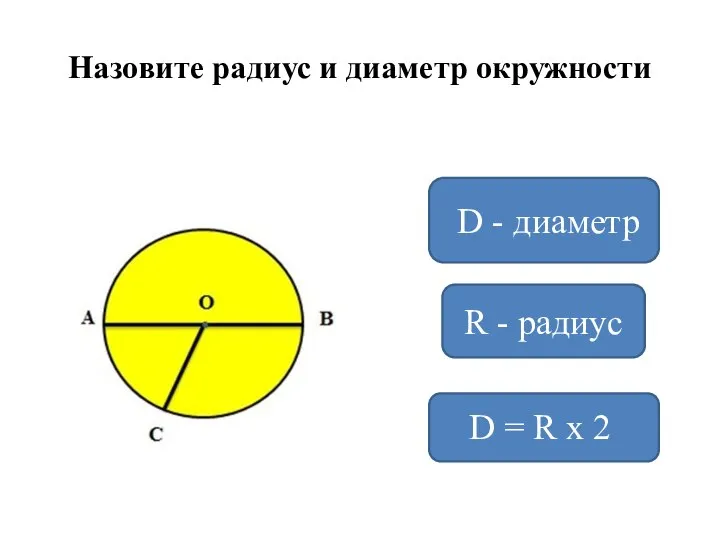 Радиус и диаметр окружности
Радиус и диаметр окружности Сочетания. Задачи
Сочетания. Задачи Единицы стоимости. Рубль, копейка
Единицы стоимости. Рубль, копейка Презентация на тему Теорема Пифагора и её применение
Презентация на тему Теорема Пифагора и её применение  Решение задач на свойства
Решение задач на свойства Приемы письменных вычислений в пределах 1000. 3 класс
Приемы письменных вычислений в пределах 1000. 3 класс Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Нахождение синуса острого угла в прямоугольном треугольнике
Нахождение синуса острого угла в прямоугольном треугольнике Сложение векторов. Сложение сил
Сложение векторов. Сложение сил Обыкновенные дроби. Задания для устного счета. 8 класс
Обыкновенные дроби. Задания для устного счета. 8 класс Презентация на тему Круг. Площадь круга
Презентация на тему Круг. Площадь круга  Вправи на засвоєння таблиці додавання і віднімання числа 7
Вправи на засвоєння таблиці додавання і віднімання числа 7 История развития обыкновенных дробей
История развития обыкновенных дробей Приемы сложения и вычитания в пределах 20 с переходом через десяток
Приемы сложения и вычитания в пределах 20 с переходом через десяток Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Углы с сонаправленными сторонами
Углы с сонаправленными сторонами Степінь з цілим показником
Степінь з цілим показником Решение планиметрических задач
Решение планиметрических задач Презентация на тему Противоположные числа (6 класс)
Презентация на тему Противоположные числа (6 класс)  Сложные проценты. Контрольная
Сложные проценты. Контрольная Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Задачи на движение
Задачи на движение Уравнение окружности
Уравнение окружности Скалярное произведение векторов
Скалярное произведение векторов Калейдоскоп заданий ОГЭ. Математическая игра
Калейдоскоп заданий ОГЭ. Математическая игра Презентация на тему Сочетательное свойство сложения
Презентация на тему Сочетательное свойство сложения  Объемы многогранников
Объемы многогранников