Содержание
- 2. фильтр фильтр фильтр фильтр фильтр фильтр фильтр фильтр фильтр
- 3. фильтр фильтр фильтр Решение задач по определению вероятности безотказной работы реальной системы на основе составления последовательно-параллельных
- 4. Рассмотрим на примере одного фильтра два несовместных события Событие «А» - фильтр полностью исправен фильтр Событие
- 5. P(А)- вероятность безотказной работы q(A)- вероятность отказа P(A)+q(A)=1 P(A)+P(A)=1 P=1-q
- 6. В ходе решения задачи необходимо составлять схему функции алгебры логики Например схема для системы состоящей из
- 7. E C A F D B S Два вида связей: горизонтальные и вертикальные При составлении уравнения:
- 8. Пример Система состоит из двух параллельных элементов «A» и «B». Из анализа функционирования системы выявлено, что
- 9. B А Решение 1. Составим структурную схему
- 10. Решение 2. Составим логическую схему A A A B B B S Оба работают Отказал B
- 11. Решение 2. Составим логическую схему A A A B B B S Оба работают Отказал B
- 12. Решение 3. Составим уравнение логики P(S)= AB+AB+AB A A A B B B S Словесная формулировка:
- 13. Решение 3. Расписываем уравнение P(S)= AB+AB+AB= =P(A)*P(B) + q(A)*P(B) + P(A)*q(B) =P(A)*P(B) + (1-P(A))*P(B) + P(A)*
- 14. B А Старый метод решения q(S)= (1-P(A))*(1-P(B)) = (1-0.7)*(1-0.9) = 0.3*0.1=0.03 q(S)= q (A)*q(B) P(S)= 1-q(s)
- 16. Скачать презентацию
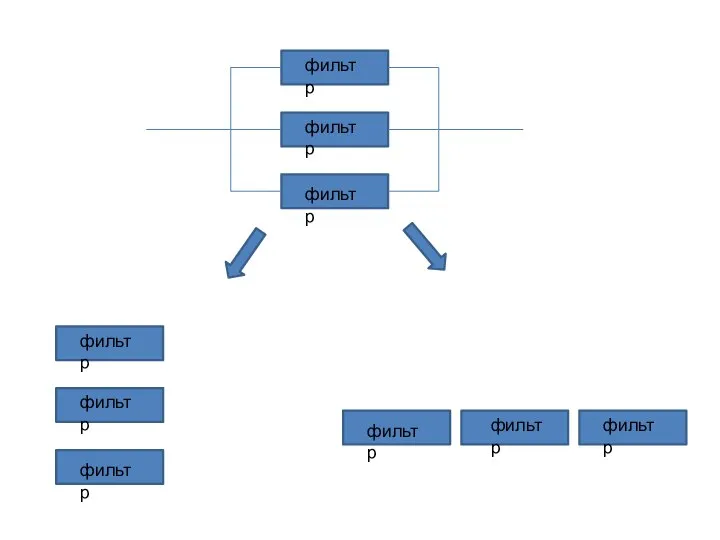
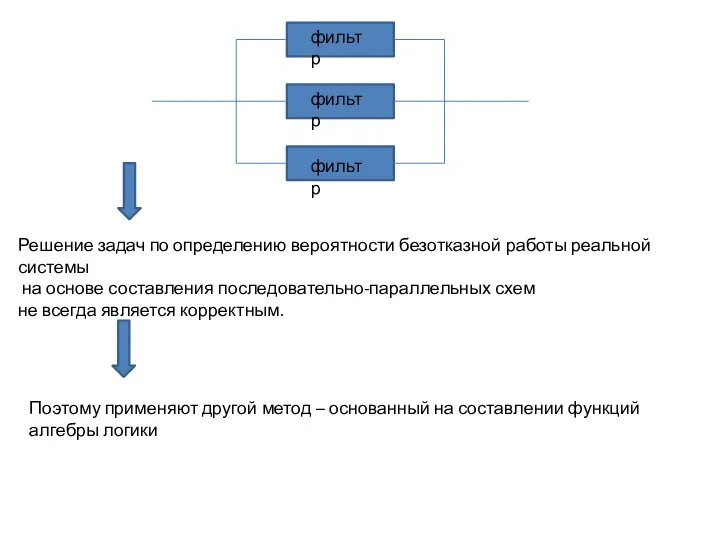

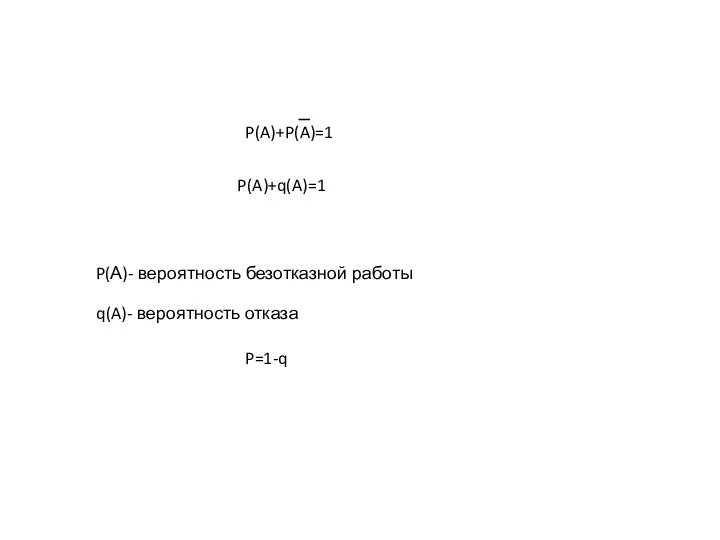
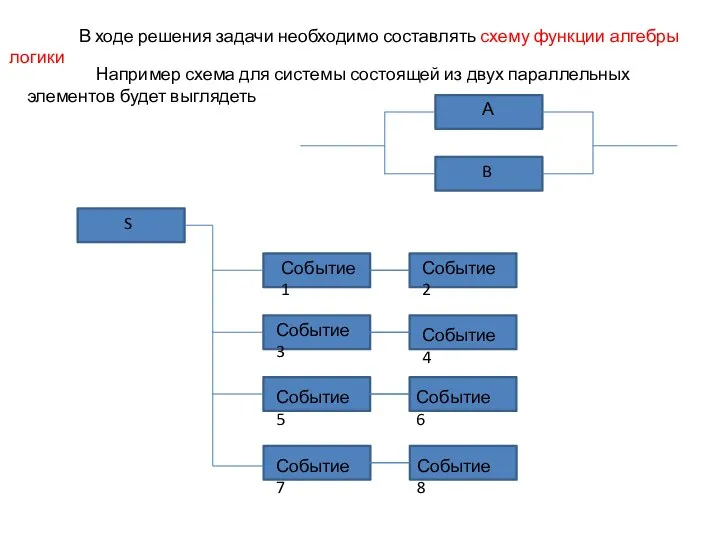
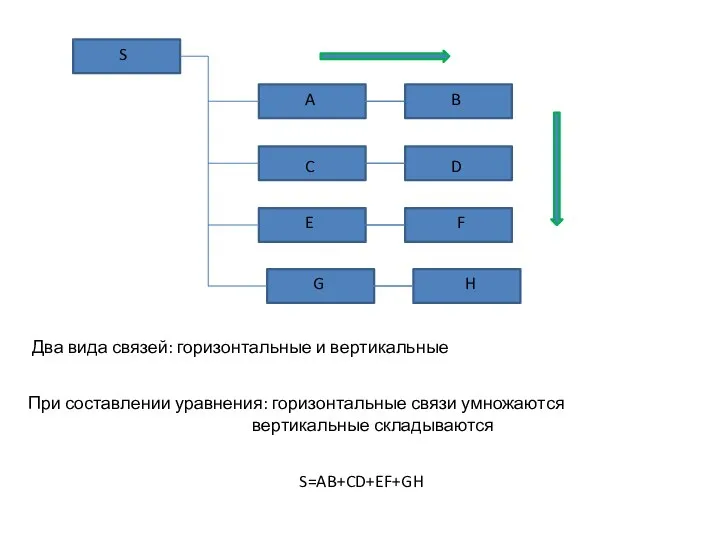
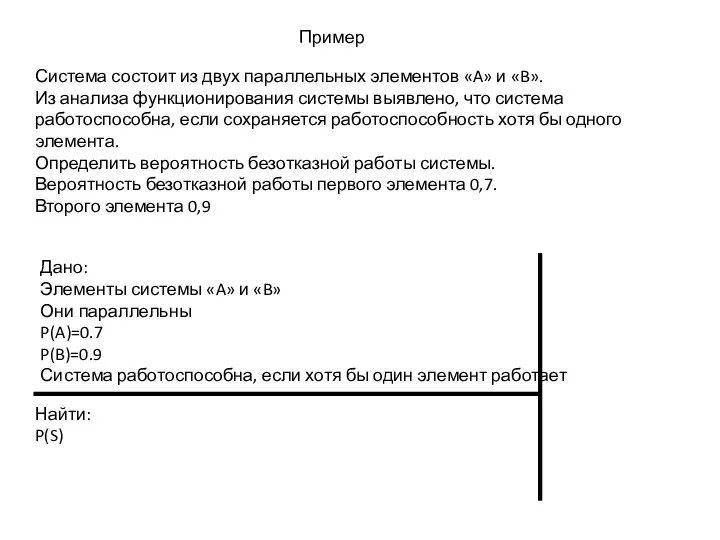
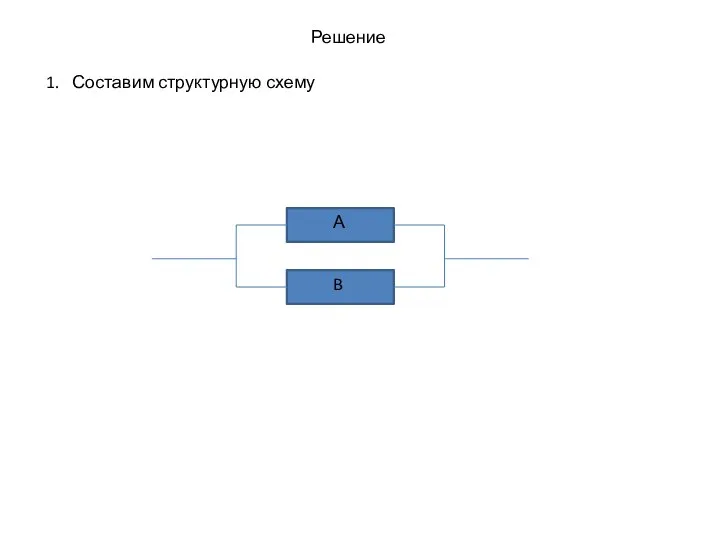
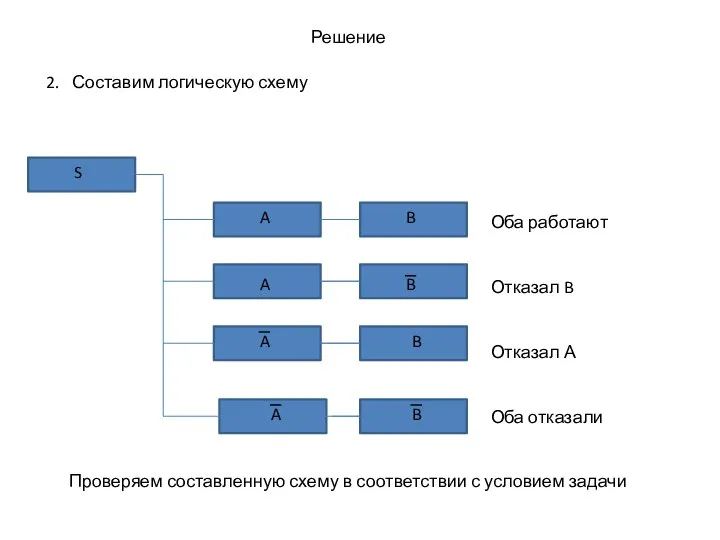
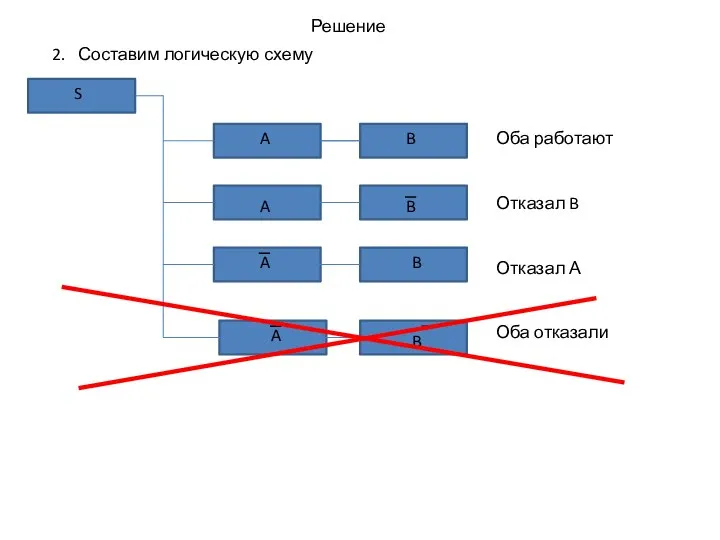
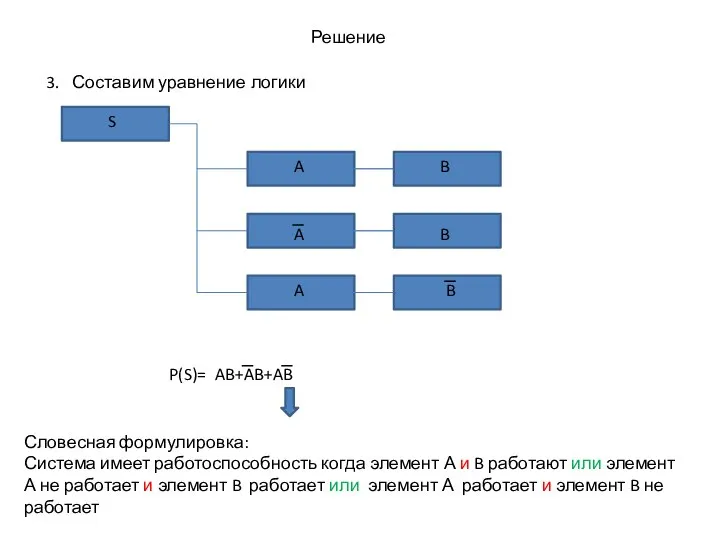

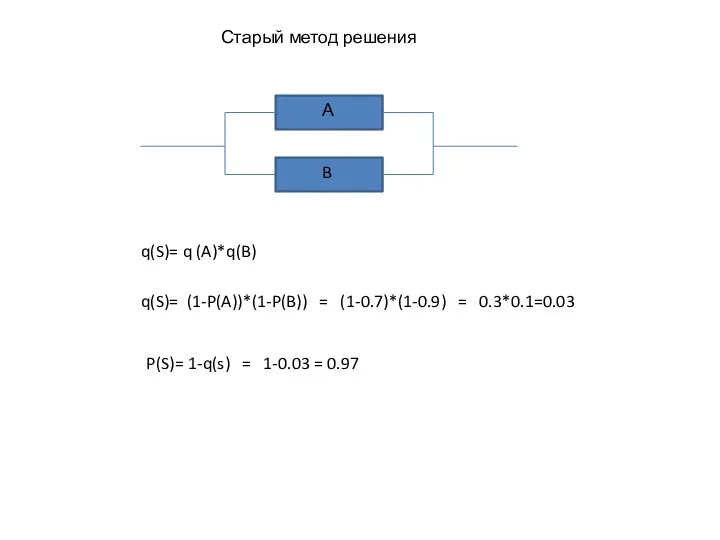
 График линейной функции
График линейной функции Презентация на тему Десятичные дроби: практикум
Презентация на тему Десятичные дроби: практикум  Уравнение касательной (Урок 101)
Уравнение касательной (Урок 101) Сравнение чисел.Часть 3. Урок 34
Сравнение чисел.Часть 3. Урок 34 Измерение длины отрезка
Измерение длины отрезка Математика. Задания на лето. Часть 4
Математика. Задания на лето. Часть 4 Призма и антипризма
Призма и антипризма Можно ли без шаблона разметить круг?
Можно ли без шаблона разметить круг? Средство измерений и их классификация
Средство измерений и их классификация Статистическое наблюдение
Статистическое наблюдение Площадь треугольника и подобие
Площадь треугольника и подобие Математикадан 5 класста үткәрелгән Тигезләмә темасын йомгаклау дәресе планы
Математикадан 5 класста үткәрелгән Тигезләмә темасын йомгаклау дәресе планы Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Вычитание смешанных чисел
Вычитание смешанных чисел Исследование функций и построение графиков
Исследование функций и построение графиков Определитель матрицы
Определитель матрицы 1_теория множеств
1_теория множеств Интегрирование функций
Интегрирование функций Решение задач
Решение задач Непрерывность функции на отрезке
Непрерывность функции на отрезке Сложение десятичных дробей
Сложение десятичных дробей Дециметр (1 класс)
Дециметр (1 класс) Геометрия вокруг нас
Геометрия вокруг нас Электронное пособие. Основные понятия и определения в математике
Электронное пособие. Основные понятия и определения в математике Известное и неизвестное
Известное и неизвестное Системы линейных алгебраических уравнений. Практикум
Системы линейных алгебраических уравнений. Практикум Геометрическая прогрессия в экономике
Геометрическая прогрессия в экономике Тренажёр Яблоки (3 класс)
Тренажёр Яблоки (3 класс)