Слайд 3Дробно – рациональная функция
Привести неправильную дробь к правильному виду:
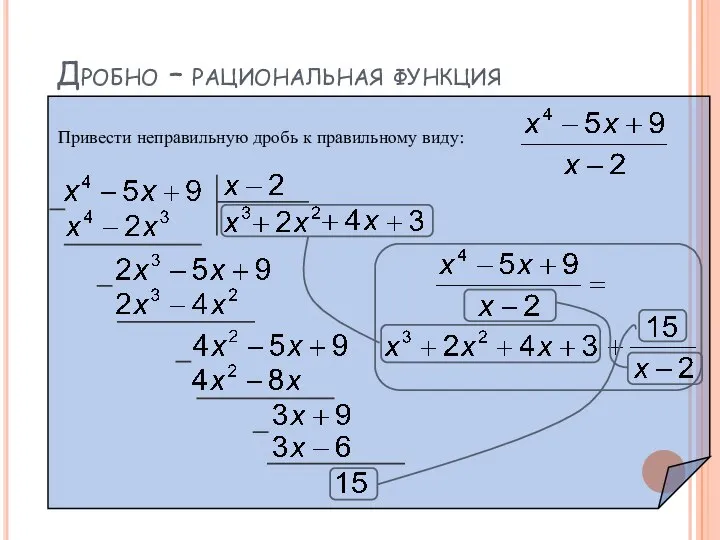
Слайд 5Интегрирование простейших дробей
Найдем интегралы от простейших рациональных дробей:
Интегрирование дроби 3 типа рассмотрим

на примере.
Слайд 8
Метод неопределенных коэффициентов

Слайд 9Теорема 1.3. Всякая рациональная дробь интегрируется в элементарных функциях.

Слайд 101.4. Интегрирование некоторых иррациональностей
m – общий знаменатель дробей α,…,γ.

Слайд 122. Определенный интеграл
Коши (1823) ввел с доступной в то время строгостью понятие

интеграла непрерывной функции как предела суммы. Риман (1854), просто как попутное замечание в своей диссертации, посвященной тригонометрическим рядам, определил интеграл для более общего класса функций. Далее мы рассмотрим теорию Римана и ее обобщения, принадлежащие Дюбуа-Реймону и Дарбу. Еще более общие теории, которые мы будем рассматривать позднее, принадлежат Лебегу (1902 г.) .
Слайд 15Определение 2.1. Число I называется пределом интегральных сумм σ(f, Δ, ξ) при

λ(Δ) → 0; если для любого положительного числа ε > 0 можно указать такое положительное число δ, что для любого разбиения Δ отрезка [a, b] , диаметр разбиения которого меньше δ: λ(Δ) < δ, независимо от выбора точек ξi на отрезках [xk,xk+1], выполняется неравенство
| σ(f, Δ, ξ) - I| < ε.
Слайд 17Теорема 2.1. Если функция интегрируема, то она ограничена.
Замечание. Ограниченность функции не гарантирует

ее интегрируемость по Риману
Слайд 20
Определение 2.3. Если разбиение Δ2 получено из разбиения Δ1 добавлением некоторого числа

узлов, то говорят, что разбиение Δ2 следует за разбиением Δ1 (или Δ2 является размельчением Δ1), при этом пишут Δ1 < Δ2 .
Слайд 225) Пусть разбиение Δ1 отрезка [а, b] получено из разбиения Δ добавлением
![5) Пусть разбиение Δ1 отрезка [а, b] получено из разбиения Δ добавлением](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/969274/slide-21.jpg)
к последнему р новых точек, и пусть s*, S* и s, S — соответственно нижние и верхние суммы разбиений Δ1 и Δ. Тогда для разностей S − S* и s* − s может быть получена оценка, зависящая от максимальной длины λ частичных сегментов разбиения Δ, числа р добавленных точек и точных верхней и нижней граней М и m функции f(x) на отрезке [а, b]. Именно,
S – S* ≤ (M - m)pλ, s* - s ≤ (М - m)рλ.




















![5) Пусть разбиение Δ1 отрезка [а, b] получено из разбиения Δ добавлением](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/969274/slide-21.jpg)

 Решение уравнений. 6 класс
Решение уравнений. 6 класс Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса Тригонометрические функции. Формулы двойного угла
Тригонометрические функции. Формулы двойного угла Графики функций у = ах2+n и y= a(x – m)2
Графики функций у = ах2+n и y= a(x – m)2 Многогранники. Призма
Многогранники. Призма Показательная функция
Показательная функция Графы. Способы задания графов. Степени вершин
Графы. Способы задания графов. Степени вершин Элементы линейной алгебры и геометрии выпуклых множеств
Элементы линейной алгебры и геометрии выпуклых множеств Таблица умножения на 2
Таблица умножения на 2 Правильные многоугольники
Правильные многоугольники Вычитание дробных чисел. 5 класс
Вычитание дробных чисел. 5 класс Презентация на тему Алгебраические уравнения произвольных степеней 10 класс
Презентация на тему Алгебраические уравнения произвольных степеней 10 класс  Периметр восьмиугольника
Периметр восьмиугольника Математичний диктант. Паралелограм
Математичний диктант. Паралелограм Векторное кодирование графической информации
Векторное кодирование графической информации Окружность
Окружность Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат Параллелепипед
Параллелепипед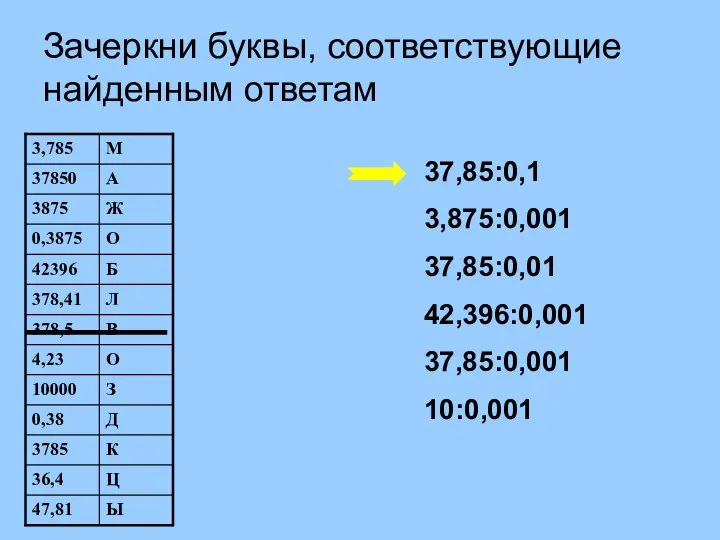 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Интерактивный тренажёр Реши уравнения
Интерактивный тренажёр Реши уравнения Элементы нелинейного функционального анализа. Гладкие многообразия
Элементы нелинейного функционального анализа. Гладкие многообразия Моделирование – способ, процесс замещения оригинала его аналогом (моделью)
Моделирование – способ, процесс замещения оригинала его аналогом (моделью) Задачи на проценты
Задачи на проценты Живая планета!
Живая планета! Квадратные уравнения
Квадратные уравнения Устный счет в пределах 10. Состав чисел 7, 8
Устный счет в пределах 10. Состав чисел 7, 8 Моделирование на графах
Моделирование на графах Стороны треугольника пропорциональны синусам противолежащих углов
Стороны треугольника пропорциональны синусам противолежащих углов