Применение производных к исследованию функций и построение графиков

План исследования функции
Область определения функции
Исследование функций на четность, нечетность
Точки пересечения с осями координат
Промежутки возрастания и убывания функции; экстремумы функции
Промежутки выпуклости и вогнутости функции; точки перегиба
Дополнительные точки, построение графика
Уравнение касательной в точке перегиба

Пример:
Исследовать функцию и построить график.
Область определения:
Исследование на четность или нечетность:
Функция общего вида, не является ни четной, ни нечетной.

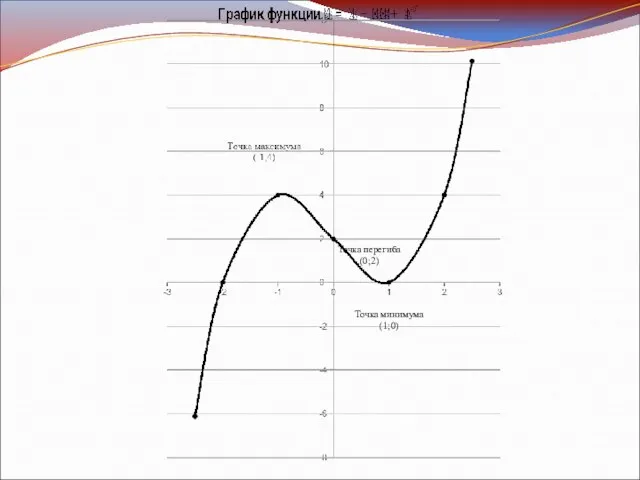
Точка пересечения с осью OX: А(1;0)
Точка пересечения с осью OY: В(0;2)
Промежутки возрастания и убывания функции, экстремумы функции:
Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции.
Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции.
Возрастание и убывание функции характеризуется знаком её первой производной.

если на некотором интервале y’>0, то функция на этом интервале возрастает;
если на некотором интервале y’<0, то функция на этом интервале убывает.
Точки, в которых первая производная равна 0 или не существует, называются критическими точками 1 рода.
Если при переходе через критическую точку x0 слева направо производная поменяла знак с + на - , то x0 называется точкой максимума функции.
Если при переходе через критическую точку x0 слева направо производная поменяла знак с - на +, то x0 называется точкой минимума функции.
Максимум и минимум функции называются её экстремумами.

Находим экстремумы функции:
Точка максимума (-1;4)
Точка минимума (1;0)
x

Промежутки выпуклости и вогнутости функции; точки перегиба:
Функция называется выпуклой, если она лежит ниже своей касательной.
Функция называется вогнутой, если она лежит выше своей касательной.
Точки, в которых выпуклость меняется на вогнутость или наоборот называются точками перегиба.
Критическими точками 2 рода называются точки, в которых 2-я производная функции равна 0 или не существует.

если на некотором интервале y’’>0, то на этом интервале график функции вогнутый;
если на некотором интервале y’’<0, то на этом интервале график функции выпуклый;
x

Находим точку перегиба:
Точка перегиба (0;2)
Дополнительные точки, построение графика:
Уравнение касательной в точке перегиба:
- уравнение касательной в точке перегиба

Точка минимума
(1;0)
Точка перегиба
(0;2)

Частной производной функции f(x,y) по переменной x в точке (x0,y0) называют предел:
Частной производной функции f(x,y) по переменной y в точке (x0,y0) называют предел:
Частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ

Пример. Найти частные производные функции