Содержание
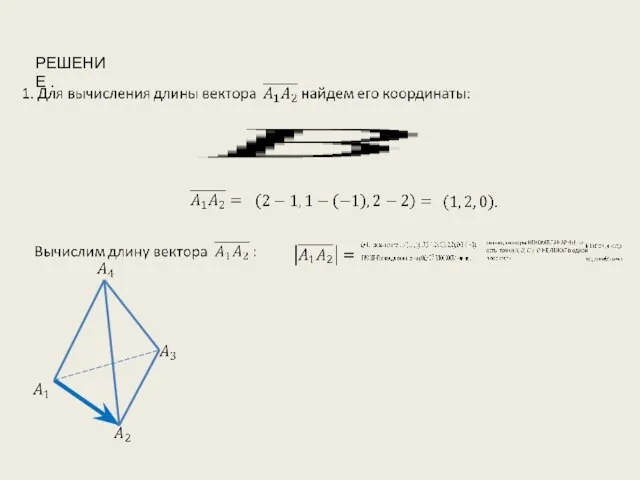
- 2. РЕШЕНИЕ .
- 3. Применим формулу для вычисления угла между векторами: Скалярное произведение в числителе получим как сумму произведений соответствующих
- 4. Модуль векторного произведения
- 5. модуля смешанного произведения векторов, образующих данную пирамиду, например, векторов Из предыдущих заданий известны их координаты: Вычислим
- 6. Н Вспомним другую формулу для вычисления этого же объема, в которой используется длина высоты пирамиды: ,
- 8. Скачать презентацию




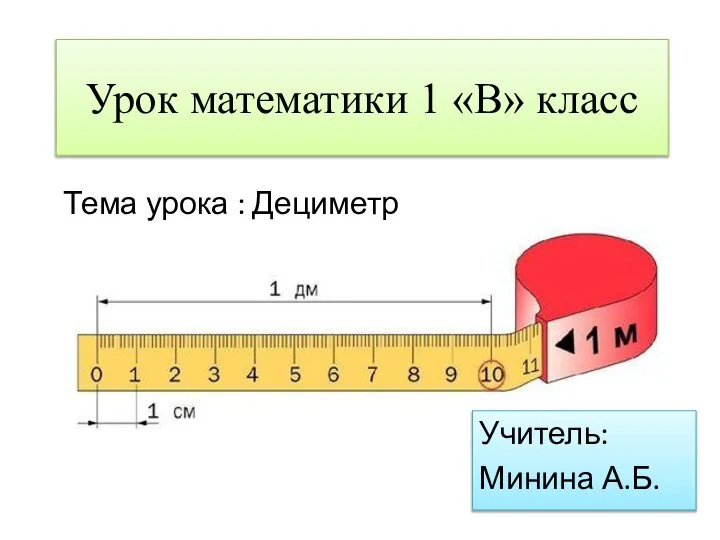 Дециметр
Дециметр Интегральные уравнения
Интегральные уравнения Умножение и деление на 2 половина числа Ученики и ученицы! Чтоб было проще вам считать, Мы Пифагорову таблицу В стихах решили напи
Умножение и деление на 2 половина числа Ученики и ученицы! Чтоб было проще вам считать, Мы Пифагорову таблицу В стихах решили напи Прибавление и вычитание числа 3. Помоги белочке
Прибавление и вычитание числа 3. Помоги белочке Дополнительный материал по геометрии к теме Треугольники
Дополнительный материал по геометрии к теме Треугольники Нестандартный урок математики. Проведен учителем I категории Крутько В.И.
Нестандартный урок математики. Проведен учителем I категории Крутько В.И. Первообразная. 11 класс
Первообразная. 11 класс Решение систем уравнений графическим и аналитическим способом
Решение систем уравнений графическим и аналитическим способом Треугольник. Изображение. Обозначение
Треугольник. Изображение. Обозначение Сложение и вычитание
Сложение и вычитание Умножение дробей
Умножение дробей История счета и систем счисления
История счета и систем счисления Аналитическая геометрия. Уравнения прямой
Аналитическая геометрия. Уравнения прямой Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс
Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс Решение задач по теме Равнобедренный треугольник
Решение задач по теме Равнобедренный треугольник Векторная алгебра
Векторная алгебра Квадратные уравнения. Основные понятия
Квадратные уравнения. Основные понятия Число е. 2,7182818284…
Число е. 2,7182818284… ЕГЭ 2014. Задачи первой и второй части (Вариант 45)
ЕГЭ 2014. Задачи первой и второй части (Вариант 45) Отношение площадей подобных треугольников
Отношение площадей подобных треугольников Opredelenny_integral
Opredelenny_integral Оптимизация функций одной переменной
Оптимизация функций одной переменной Многовариантные планиметрические задачи: взаимное расположение фигур
Многовариантные планиметрические задачи: взаимное расположение фигур Логарифм числа и его свойства
Логарифм числа и его свойства Второй признак равенства треугольников. Теорема
Второй признак равенства треугольников. Теорема Математика. Число 10 (1 класс)
Математика. Число 10 (1 класс)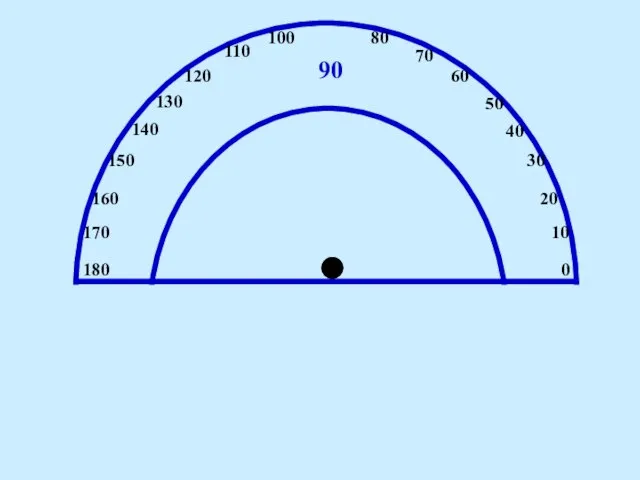 Презентация на тему Транспортир
Презентация на тему Транспортир  Решение задач на перебор вариантов
Решение задач на перебор вариантов