Содержание
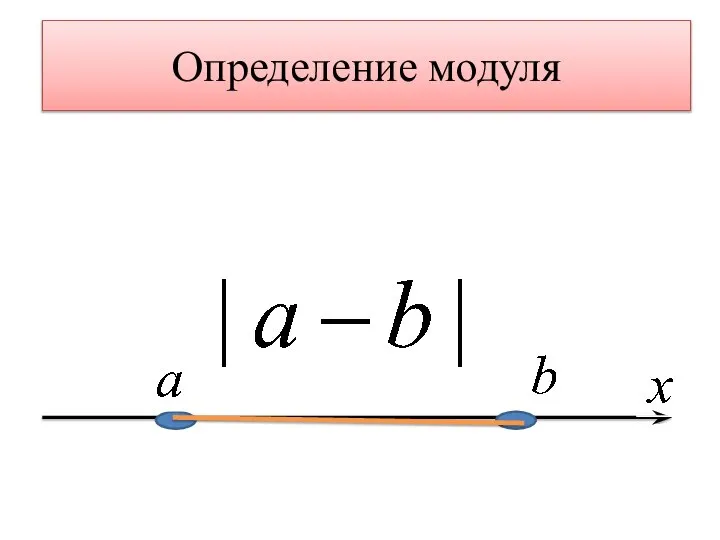
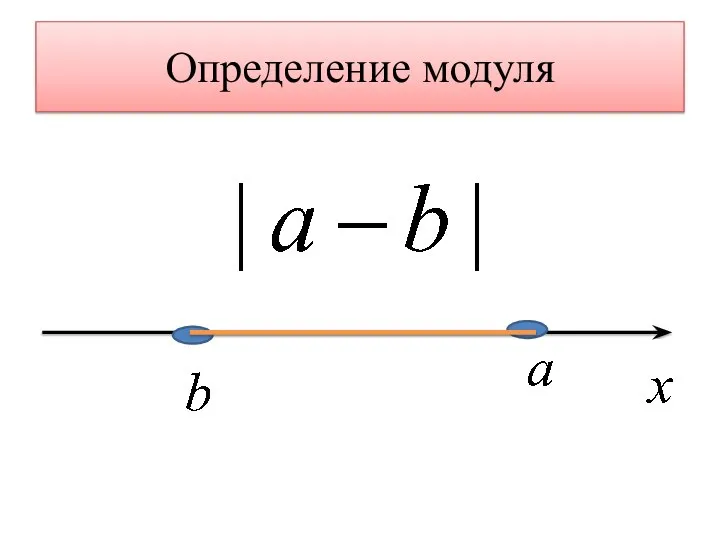
- 2. Определение модуля
- 3. Определение модуля
- 4. Определение модуля
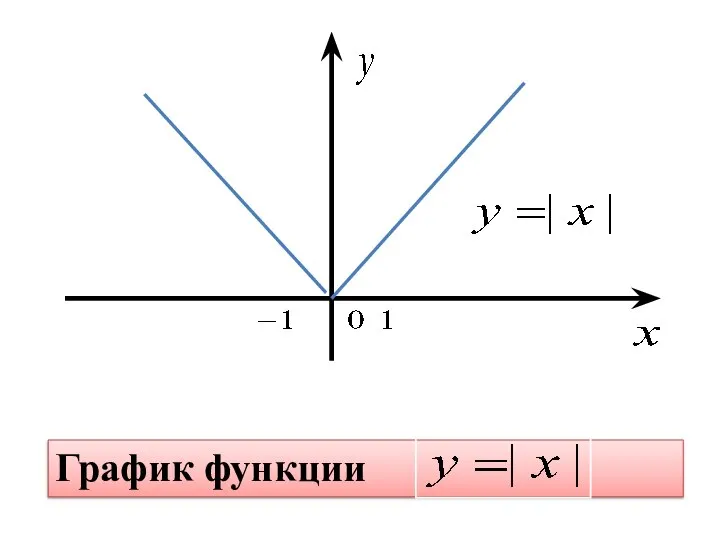
- 5. График функции
- 6. Решение уравнений с модулем
- 7. Решите уравнения:
- 8. Решение уравнений с модулем
- 9. Решите уравнения:
- 10. Решение уравнений с модулем
- 11. Решите уравнения:
- 12. Решите уравнение:
- 13. Задание на дом
- 14. 6 способов решения одного уравнения
- 15. Уравнение с модулем Решить уравнение Решение: Для раскрытия двух модулей рассмотрим следующие 4 случая: Найдем нули
- 16. или или или
- 17. Решений нет Решений нет Ответ: [-1;3]
- 18. Решите уравнение II способ. Так как обе части уравнения неотрицательные, то при возведении их в квадрат
- 19. III способ - графический Перепишем данное уравнение в следующем виде: Далее изобразим графики функций И укажем
- 20. III способ - графический Ответ: [-1;3]
- 21. IVспособ - графический Найдем абсциссы общих точек графика функции и прямой Для построения первого графика достаточно
- 22. Ответ: [-1;3] IVспособ - графический
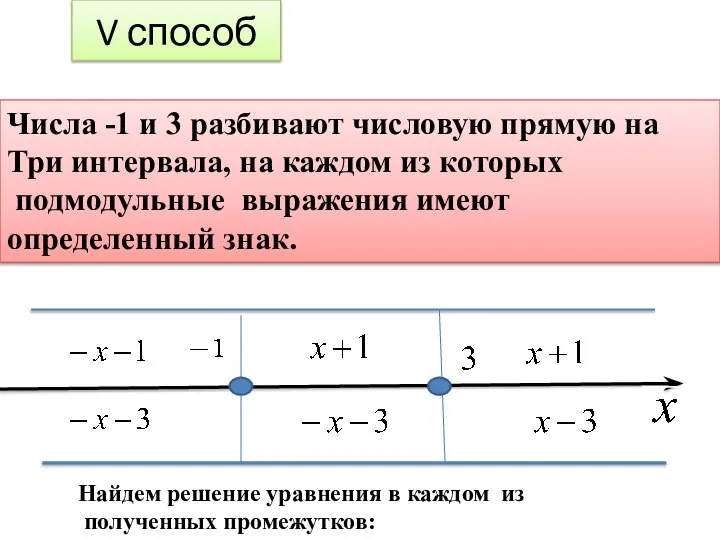
- 23. V способ Числа -1 и 3 разбивают числовую прямую на Три интервала, на каждом из которых
- 24. или или
- 25. Нет решения Ответ: [-1;3]
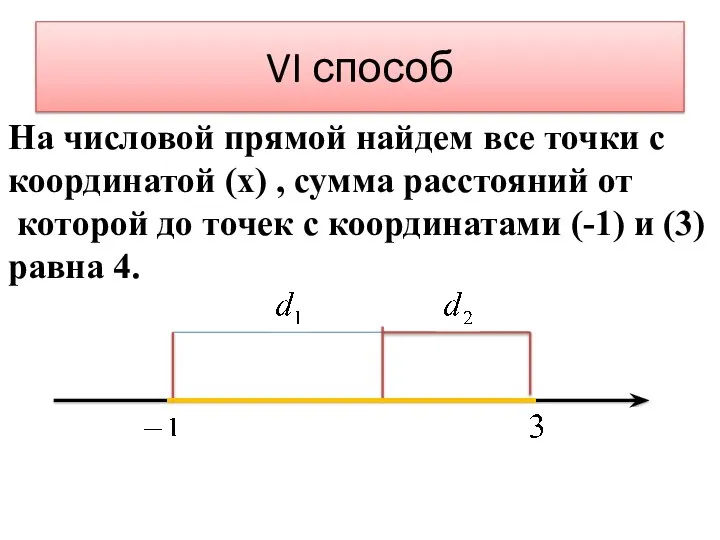
- 26. VI способ На числовой прямой найдем все точки с координатой (х) , сумма расстояний от которой
- 28. Скачать презентацию











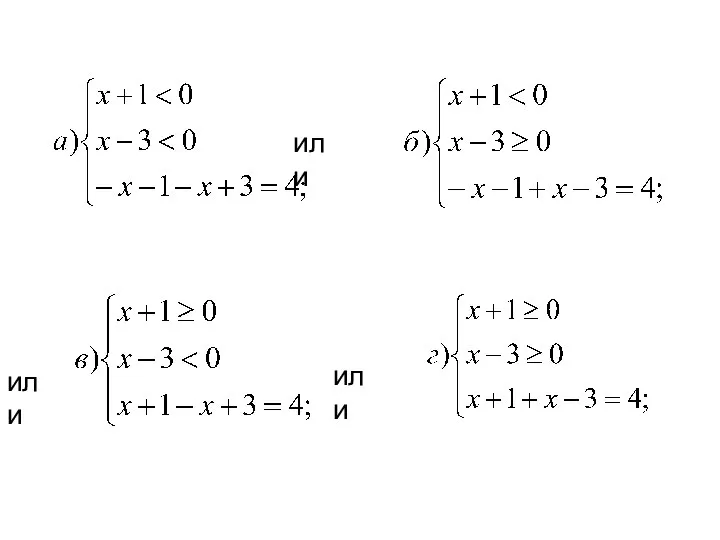
![Решений нет Решений нет Ответ: [-1;3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1161917/slide-16.jpg)


![III способ - графический Ответ: [-1;3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1161917/slide-19.jpg)

![Ответ: [-1;3] IVспособ - графический](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1161917/slide-21.jpg)
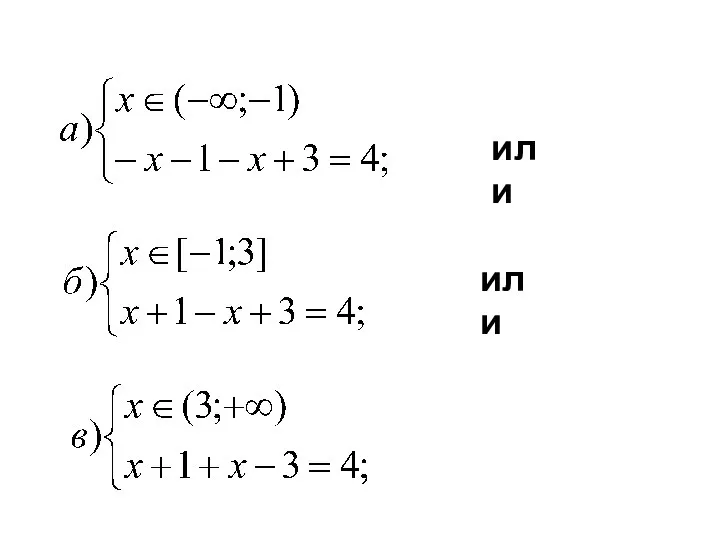
![Нет решения Ответ: [-1;3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1161917/slide-24.jpg)
 Первый признак подобия треугольников. Решение задач
Первый признак подобия треугольников. Решение задач Комбінаторика, як розділ математики. Сполуки без повторень. Найпростіші комбінаторні задачі
Комбінаторика, як розділ математики. Сполуки без повторень. Найпростіші комбінаторні задачі Тригонометрия. Математика с Д.А. Власовым
Тригонометрия. Математика с Д.А. Власовым Устная работа. Как обозначают и сравнивают углы
Устная работа. Как обозначают и сравнивают углы Равенство, неравенство. Устный счет (1 класс)
Равенство, неравенство. Устный счет (1 класс) Системы степенных неравенств
Системы степенных неравенств Введение в геометрию
Введение в геометрию Координатная плоскость
Координатная плоскость Транспортная задача. Методы нахождения начального решения транспортной задачи
Транспортная задача. Методы нахождения начального решения транспортной задачи Цифры в загадках и пословицах
Цифры в загадках и пословицах Определение и содержание математического программирования как математической дисциплины
Определение и содержание математического программирования как математической дисциплины Свойства показательной функции
Свойства показательной функции Арифметическая прогрессия
Арифметическая прогрессия Логарифм числа
Логарифм числа Дискретная математика. Основные понятия и определения графа и его элементов
Дискретная математика. Основные понятия и определения графа и его элементов Взаимно перпендикулярные и параллельные геометрические образы
Взаимно перпендикулярные и параллельные геометрические образы Поле чудес. Геометрия
Поле чудес. Геометрия Системы счисления
Системы счисления Урок сюрприз. Величины
Урок сюрприз. Величины Классификация: общие принципы
Классификация: общие принципы Планирование эксперимента при проектировании РЭС
Планирование эксперимента при проектировании РЭС Самостоятельная работа
Самостоятельная работа Methodical Problems of Comparative Studies
Methodical Problems of Comparative Studies Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Алан Тьюринг
Алан Тьюринг Презентация учебного проекта Автор: Зрянина Татьяна Ивановна, учитель математики
Презентация учебного проекта Автор: Зрянина Татьяна Ивановна, учитель математики Нахождение неизвестного уменьшаемого, неизвестного вычитаемого
Нахождение неизвестного уменьшаемого, неизвестного вычитаемого Презентация на тему Дробные рациональные уравнения
Презентация на тему Дробные рациональные уравнения