Решение задач с параметрами

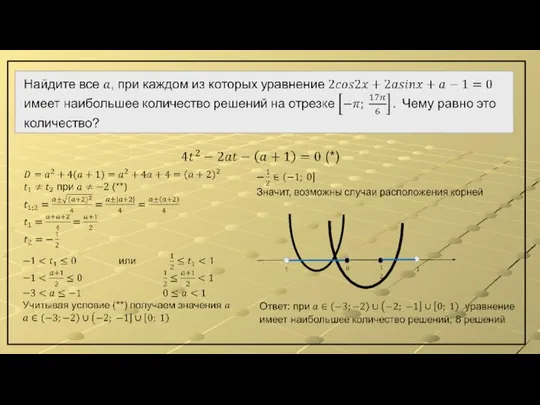
Таким образом, наибольшее количество решений 8 заданное уравнение будет иметь, если уравнение (*) будет иметь два различных корня, удовлетворяющих третьему условию

С учетом ОДЗ параметра решаем систему

Рассмотрим случаи, когда основание логарифма больше 1 или принимает значения от 0 до 1

Заданное уравнение будет равносильно совокупности следующих систем:

Решим систему (**)