Содержание
- 2. Актуальность исследования С XX века числа Фибоначчи стали одним из наиболее популярных объектов для исследования, привлекая
- 3. Цели работы: Определение последовательности Фибоначчи ; Изучение наиболее важных свойств чисел Фибоначчи; Изучение сфер применения ряда
- 4. Предмет исследования: Последовательность чисел Фибоначчи. 1. Поиск и анализ литературного материала Методы исследования 2. Эмпирическое исследование
- 5. Кто такой Фибоначчи? Леонардо Пизанский, известный под псевдонимом Фибоначчи, - первый известный математик средневековой Европы. Он
- 6. Решение задачи: Из условия известно, что в начале февраля в огороженном месте будет две пары кроликов,
- 7. Основные свойства последовательности Фибоначчи Сумма первых n членов числового ряда Фибоначчи равна F(n + 2) –
- 8. Семена в цветках подсолнуха располагаются по спирали Фибоначчи, количество этих спиралей – это два последовательных члена
- 9. Испуганное стадо оленей разбегается по спирали Фибоначчи.
- 10. Млечный путь, как и многие другие галактики, имеет форму спирали Фибоначчи
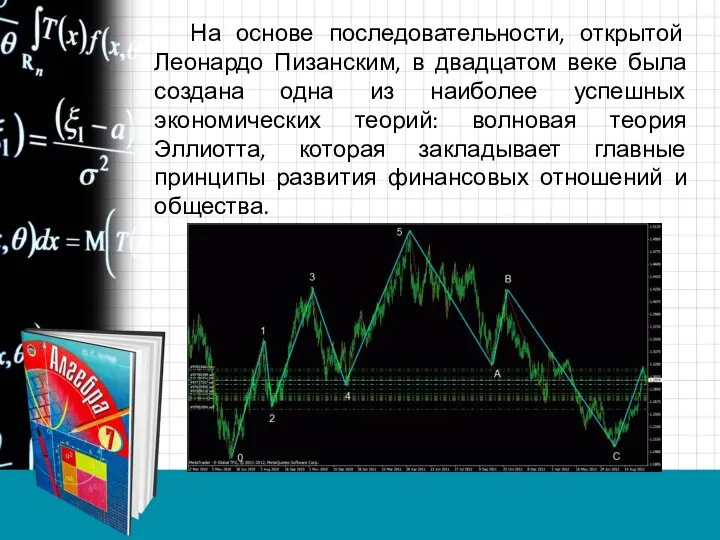
- 11. На основе последовательности, открытой Леонардо Пизанским, в двадцатом веке была создана одна из наиболее успешных экономических
- 12. Таким образом, изучение последовательности Фибоначчи позволяет несколько упорядочить собственные знания по строению мироздания, потому что, по
- 14. Скачать презентацию










 Понятие функции
Понятие функции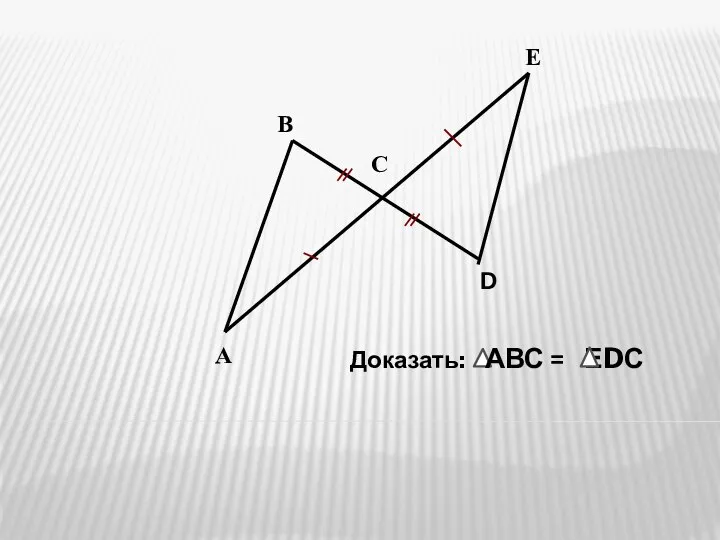 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач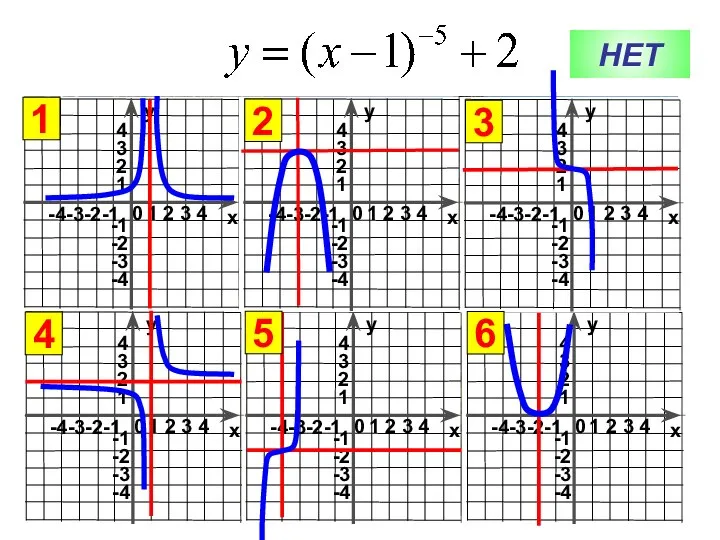 графики функций. Ошибка
графики функций. Ошибка Методы решения Слау. Метод Гаусса
Методы решения Слау. Метод Гаусса Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Приложение производной
Приложение производной Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс) Допуски линейных размеров. Квалитет
Допуски линейных размеров. Квалитет Симметрия в природе
Симметрия в природе Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Числовой коэффициент
Числовой коэффициент Квадратные уравнения. Устная разминка
Квадратные уравнения. Устная разминка Формула Стирлинга
Формула Стирлинга Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Тригонометрические уравнения
Тригонометрические уравнения Сравнение двух прогрессий
Сравнение двух прогрессий Математика. Составные высказывания
Математика. Составные высказывания Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой Некоторые понятия о статистике, статистическом методе и термодинамике
Некоторые понятия о статистике, статистическом методе и термодинамике Математическая викторина (начальная школа)
Математическая викторина (начальная школа) Координатный луч
Координатный луч Векторы плоскости
Векторы плоскости Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Площади четырёхугольников. Решение задач
Площади четырёхугольников. Решение задач Математика и физика здоровья
Математика и физика здоровья Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого