Prezentatsia_k_uroku_matematiki_6_klass

Ломаная
Ломаная линия лежит в основе построения многоугольника.
Построим ломаную. Для этого отметим на плоскости несколько точек – например, пять. Соединим их так, чтобы никакие два из отрезков, имеющих общие точки, не лежали на одной прямой. Полученная фигура и будет ломаной, которую обозначают A, B, C, D, E.
Отрезки АВ, ВС, СD,DE называются звеньями ломаной. У ломаной, которую мы изобразили, четыре звена.

Длина ломаной
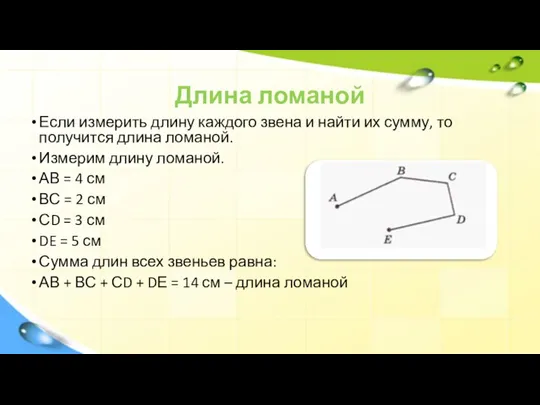
Если измерить длину каждого звена и найти их сумму, то получится длина ломаной.
Измерим длину ломаной.
АВ = 4 см
ВС = 2 см
СD = 3 см
DE = 5 см
Сумма длин всех звеньев равна:
АВ + ВС + СD + DЕ = 14 см – длина ломаной

Многоугольник
Теперь нарисуем ломаную таким образом, чтобы её конец совпадал с началом. Получается замкнутая ломаная A, B, C, D, E, А.
Фигуру, образованную таким образом, называют многоугольником. То есть многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.
Стоит помнить, что многоугольником является как замкнутая линия, так и эта линия вместе с плоскостью внутри неё.

Элементы многоугольника
Такие звенья называются сторонами многоугольника. В нашем случае это стороны АВ, ВС, СD,DE, ЕА.
Углы, образованные двумя соседними сторонами, называют углами многоугольника, а их вершины – вершинами многоугольника.
∠А, ∠В, ∠С, ∠D, ∠E – углы многоугольника
Точки А, В, С, D, E – вершины многоугольника
Кроме того, у многоугольника есть ещё и диагонали.
Диагональ – это отрезок, соединяющий две несмежные вершины многоугольника. АС, СЕ – диагонали.
Сумма всех сторон многоугольника составляет периметр многоугольника.
P = АВ + ВС + СD + DЕ + ЕА

Виды многоугольников
Рассмотрим разновидности многоугольников.
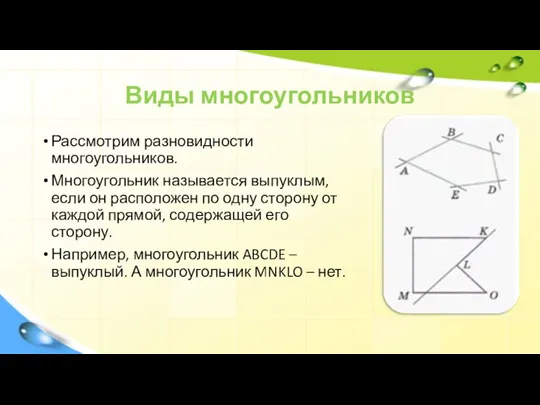
Многоугольник называется выпуклым, если он расположен по одну сторону от каждой прямой, содержащей его сторону.
Например, многоугольник ABCDE – выпуклый. А многоугольник MNKLO – нет.

Виды многоугольников
По числу сторон многоугольники делятся на треугольники, пятиугольники и так далее.
Кроме того, многоугольники, у которых все стороны и все углы равны, называют правильными. Например, квадрат.
Многоугольники можно сравнить путём наложения. Если они полностью накладываются друг на друга, то считаются равными. При этом стоит помнить, они имеют одинаковые площади.

Треугольник
Треугольник – наименьшая возможная замкнутая ломаная.
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

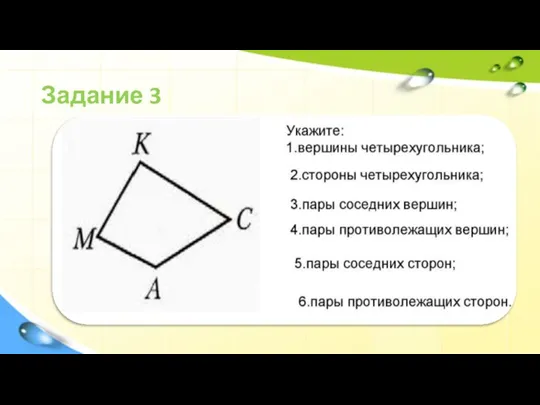
Четырехугольник
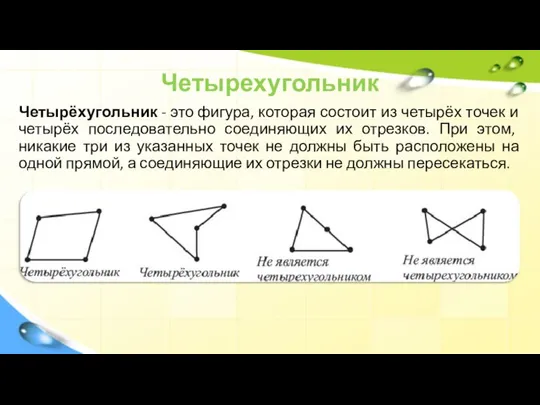
Четырёхугольник - это фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом, никакие три из указанных точек не должны быть расположены на одной прямой, а соединяющие их отрезки не должны пересекаться.

Четырехугольник
Данные точки называются вершинами четырёхугольника, а соединяющие их отрезки - сторонами четырёхугольника.

Четырехугольник
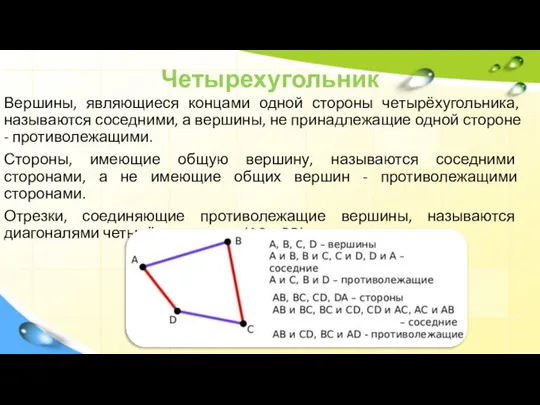
Вершины, являющиеся концами одной стороны четырёхугольника, называются соседними, а вершины, не принадлежащие одной стороне - противолежащими.
Стороны, имеющие общую вершину, называются соседними сторонами, а не имеющие общих вершин - противолежащими сторонами.
Отрезки, соединяющие противолежащие вершины, называются диагоналями четырёхугольника. (AC и BD)

Круг и окружность

Домашние задания

Задание 1
Длина первого звена ломаной 10 см. Длина каждого следующего на 2 см больше предыдущего. Зная, что в этой ломаной три звена, найдите её длину.

Задание 2
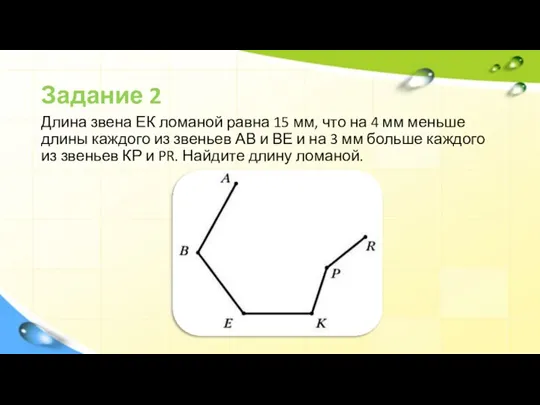
Длина звена ЕК ломаной равна 15 мм, что на 4 мм меньше длины каждого из звеньев АВ и ВЕ и на 3 мм больше каждого из звеньев КР и PR. Найдите длину ломаной.

Задание 3