Слайд 2План вебинара
Разбор ДЗ.
Ряды.
2.1) Сходимость (знакоположительные; знакопеременные ряды).
2.2) Ряды Тейлора и Маклорена.
2.3)

Ряд Фурье.
Слайд 3Общие моменты
Важны и необходимое, и достаточное условие экстремума.
Локальный экстремум не обязательно совпадает

с наибольшим или наименьшим значениями функции.
Слайд 6Минимум
Максимум
Иллюстрация задачи на максимум: https://www.wolframalpha.com/input/?i=maximize+3-8x%2B6y+on+x%5E2%2By%5E2%3D36

Слайд 9Максимум
Минимум
Минимум
Максимум

Слайд 10Графики
Задача максимизации:
https://www.wolframalpha.com/input/?i=maximize+2x%5E2%2B12xy%2B32y%5E2%2B15+on+x%5E2%2B16y%5E2%3D64
Задача минимизации:
https://www.wolframalpha.com/input/?i=minimize+2x%5E2%2B12xy%2B32y%5E2%2B15+on+x%5E2%2B16y%5E2%3D64

Слайд 18Числовой ряд – это бесконечная сумма

Слайд 19Сходимость ряда
Если ряд сходится, мы можем найти сумму ряда.
Т.е. сумма не

растет до бесконечности, а складывается в определенное число.
Слайд 20Зачем нужны ряды
Способ исследовать и аппроксимировать функцию (приблизительно описать).

Слайд 23Если необходимое условие выполняется,
то ряд может сходиться и нужны дополнительные исследования (достаточное

условие).
Если необходимое условие не выполняется, то ряд точно не сходится.
Необходимые условия нужны, чтобы отсеять наверняка не сходящиеся ряды.
Но окончательный положительный ответ про сходимость по необходимому условию мы дать не можем.
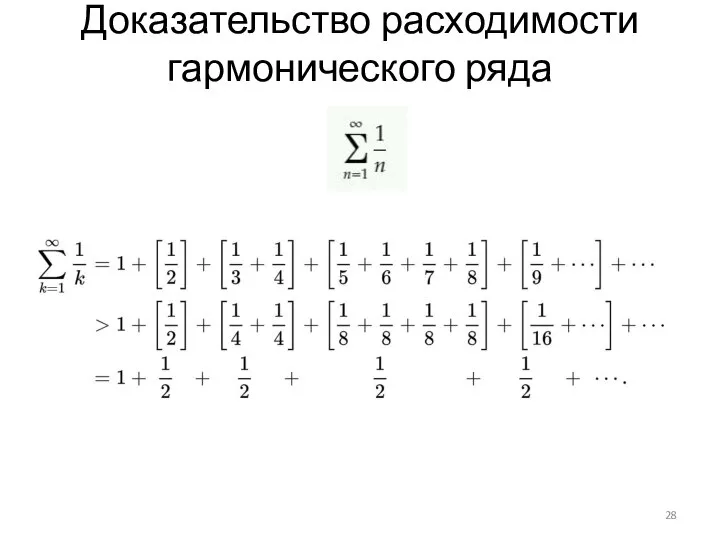
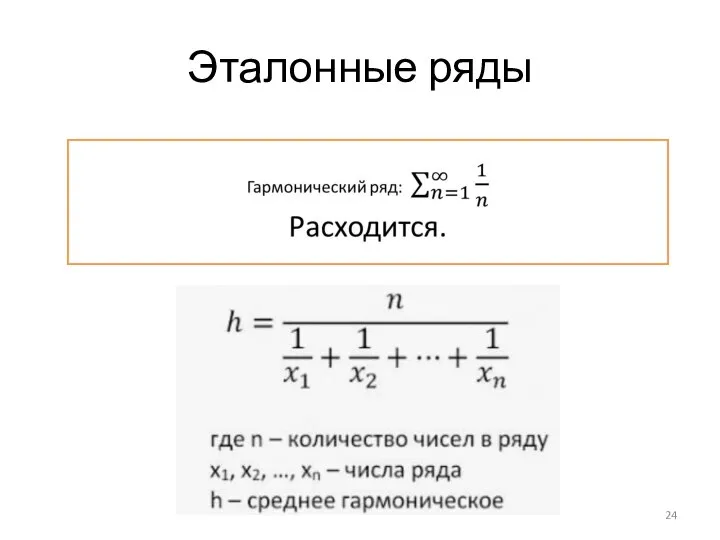
Слайд 27Доказательство расходимости гармонического ряда

Слайд 28Доказательство расходимости гармонического ряда
Слайд 29Признак=необходимое условие + достаточное условие

Слайд 312-й признак сравнения
(предельный)

Слайд 36Сильный признак, но не всесильный:
q=1 => нужны дополнительные исследования.

Слайд 38Самый популярный признак, но
при q=1 нужны дополнительные исследования.

Слайд 41Радикальный признак Коши. Пример.

Слайд 42Радикальный признак Коши. Пример.
0<1 -> ряд сходится

Слайд 43Признак Раабе
Источник: http://mathprofi.ru/slozhnye_ryady.html

Слайд 45Несобственные интегралы. Дополнение.
Дан несобственный интеграл:

Слайд 46Интегральный признак Коши
Данный ряд сходится одновременно с несобственным интегралом:
То есть, если такой

интеграл можно посчитать, и он не равен бесконечности, ряд сходится.
Слайд 47Исследовать ряд с помощью интегрального признака Коши
Для этого нужно посчитать интеграл:

Слайд 48Исследовать ряд с помощью интегрального признака Коши
Для этого нужно посчитать интеграл:

Слайд 49Исследовать ряд с помощью интегрального признака Коши
Для этого нужно посчитать интеграл:
!замена пределов

интегрирования при замене переменной!
Слайд 50Интеграл расходится, следовательно расходится и ряд.

Слайд 53Для этого найдём интеграл
!замена пределов интегрирования при замене переменной!

Слайд 54Интеграл сходится, следовательно ряд тоже сходится.

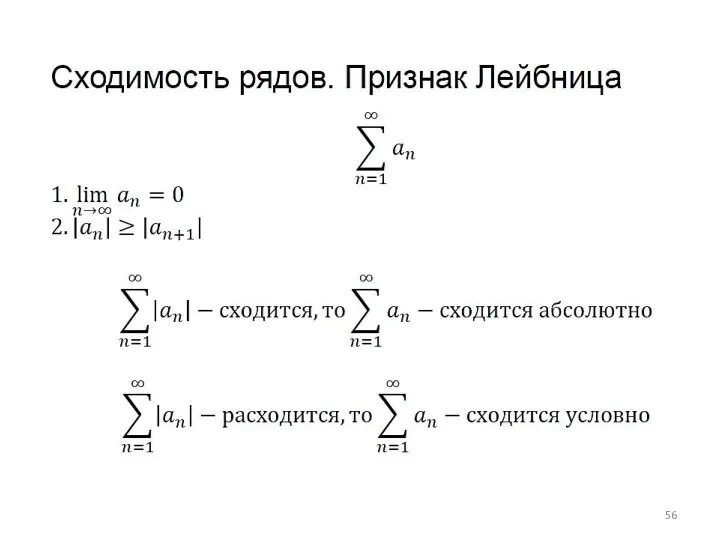
Слайд 55Сходимость рядов: знакочередующиеся ряды

Слайд 59=
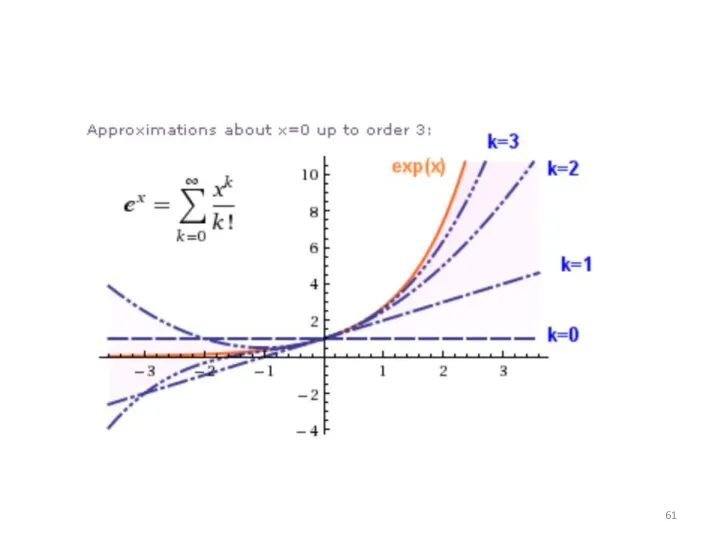
Используются для аппроксимации функции многочленами

Слайд 63Ряд Маклорена (ряд Тейлора в окрестности точки 0)

Слайд 68https://mipav.cit.nih.gov/pubwiki/index.php/Fast_Fourier_Transformation_(FFT)
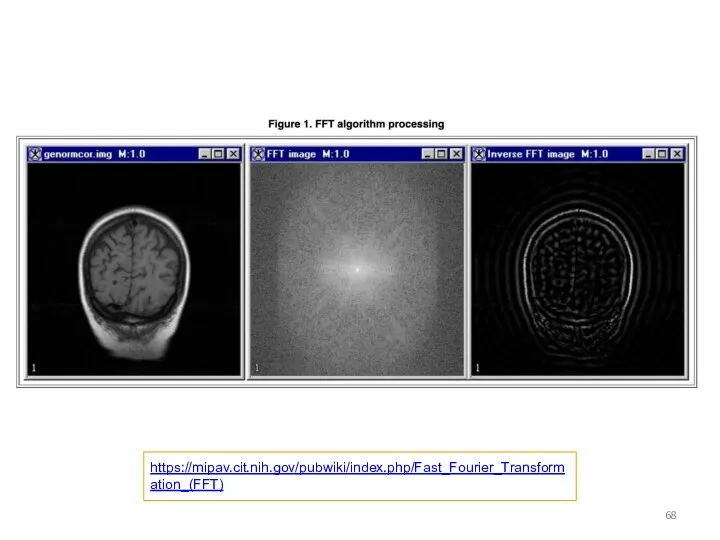
Слайд 69Fast Fourier transformation (FFT).
Применяются в аудио формате .mp3.
До этого формата

аудио дорожка хранилась в виде массива времени и значения амплитуды звуковой волны.
В формате .mp3 хранятся уже коэффициенты FFT. При этом существо сокращается место на хранение звуковой дорожки. Все современные мультимедийные форматы, особенно работающие в Интернете, как правило, построены на FFT.

























































 Занимательная математика
Занимательная математика Способы решения квадратных уравнений
Способы решения квадратных уравнений Презентация. Цилиндр
Презентация. Цилиндр Coordinate plane
Coordinate plane Графы
Графы Расстояние между точкой и прямой
Расстояние между точкой и прямой Презентация на тему Решение уравнений высших степеней
Презентация на тему Решение уравнений высших степеней  Симметрия в пространстве
Симметрия в пространстве Умножение и деление десятичной дроби на единицу с нулями
Умножение и деление десятичной дроби на единицу с нулями Теоремы синусов и косинусов
Теоремы синусов и косинусов 2_Calculations
2_Calculations Решение задач всех типов на обыкновенные дроби
Решение задач всех типов на обыкновенные дроби Игра-конкурс
Игра-конкурс Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Происхождение неевклидовой геометрии
Происхождение неевклидовой геометрии Проецирование точки
Проецирование точки Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними Метод Ньютона
Метод Ньютона История аксиомы
История аксиомы Полезные витамины
Полезные витамины Решение показательных неравенств
Решение показательных неравенств Решение уравнений
Решение уравнений Сечение тетраэдра
Сечение тетраэдра Прямая Эйлера
Прямая Эйлера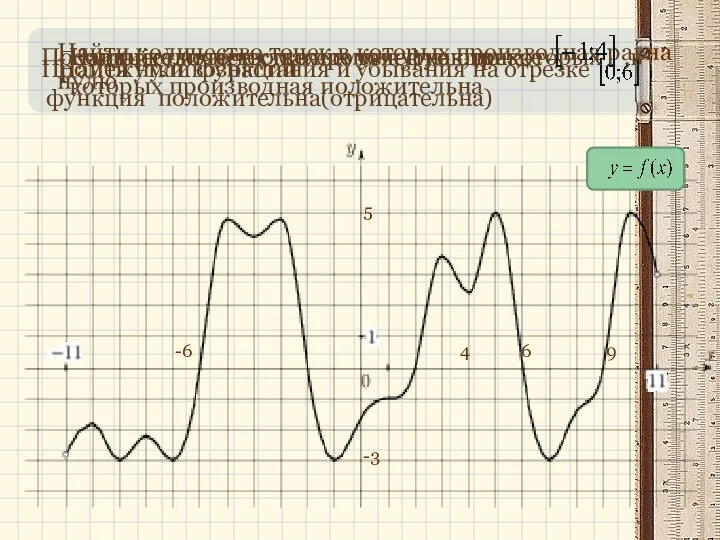 Алгоритм нахождения интервалов выпуклости и точек перегиба
Алгоритм нахождения интервалов выпуклости и точек перегиба Золотое сечение
Золотое сечение Пушкин и математика
Пушкин и математика