Нахождение коэффициентов квадратичной функции по графику

ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ
ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
Коэффициент а влияет на направление ветвей параболы:
при а > 0 – ветви направлены вверх,
при а < 0 – вниз.
2) Коэффициент b влияет на расположение вершины параболы относительно оси ОУ.
При b = 0 вершина лежит на оси ОУ.
3) Коэффициент с показывает точку пересечения параболы с осью ОУ.

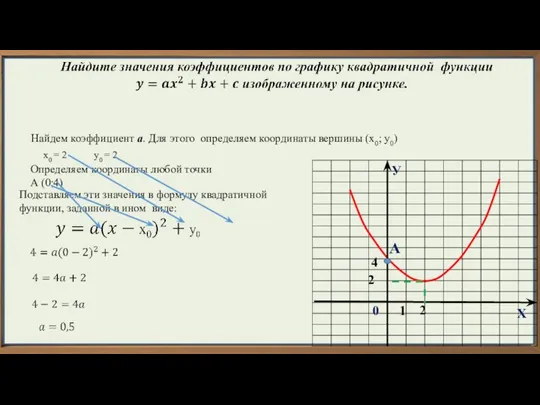
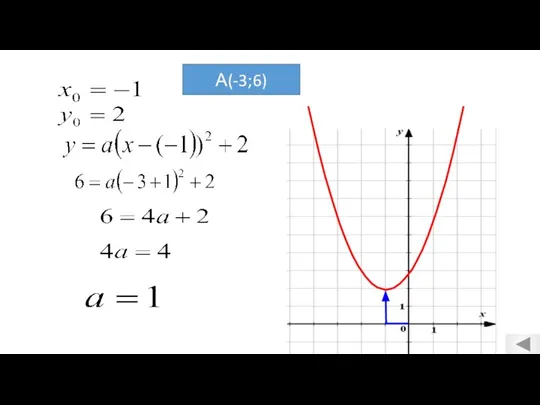
У
Х
1
2
0
А
4
Найдем коэффициент а. Для этого определяем координаты вершины (х0; у0)
2
х0 = 2
у0 = 2
Определяем координаты любой точки
А (0;4)
Подставляем эти значения в формулу квадратичной функции, заданной в ином виде:

Нахождение коэффициента а:
1) по графику параболы определяем координаты вершины
(х0, у0)
2) по графику параболы определяем координаты любой точки А(х1;у1)- те, которые имеют целые значения
3) подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
y=a(х-х0)2+у0
4) решаем полученное уравнение.

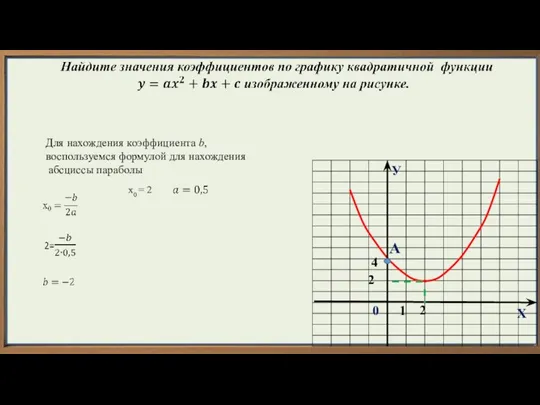
У
Х
1
2
0
А
4
2
Для нахождения коэффициента b,
воспользуемся формулой для нахождения
абсциссы параболы
х0 = 2

Нахождение коэффициента b:
1.Сначала находим координаты вершины параболы и значение коэффициента a(алгоритм 1)
2.В формулу для абсциссы параболы х0= -b/2a подставляем значения х0 и a
3.Находим значение коэффициента b.

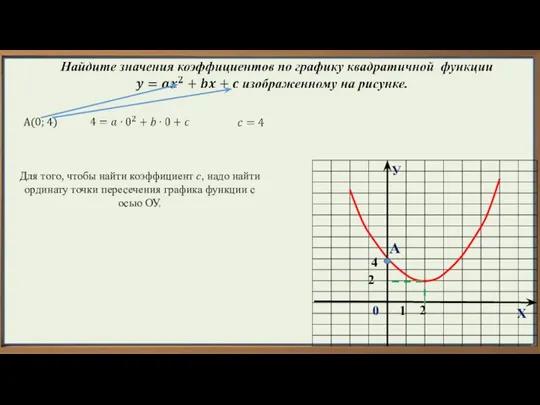
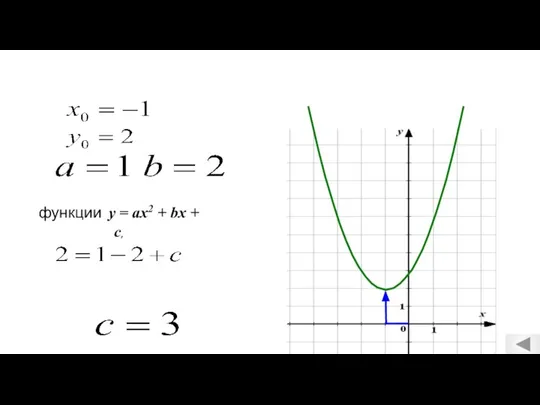
У
Х
1
2
0
А
4
А(0; 4)
Для того, чтобы найти коэффициент c, надо найти ординату точки пересечения графика функции с осью ОУ.
2

Нахождение коэффициента с:
1.Находим ординату у точки пересечения параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;с) - точка пересечения параболы с осью Оу.
2.Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II (находим коэффициенты a, b)
3.Подставляем найденные значения a, b , А(х1 ;у1) в уравнение у=ax2 +bx+c и находим с.

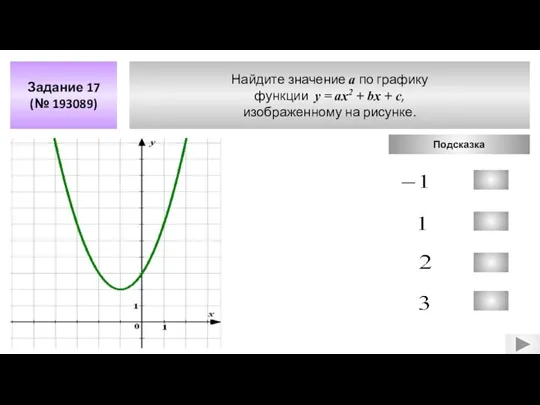
Найдите значение а по графику
функции у = aх2 + bx + c,
изображенному на рисунке.
Задание 17
(№ 193089)
Подсказка

А(-3;6)

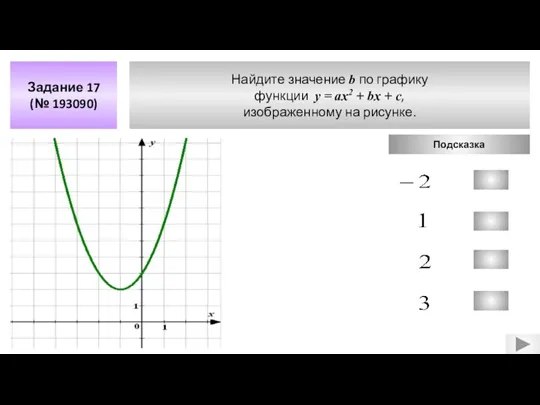
Найдите значение b по графику
функции у = aх2 + bx + c,
изображенному на рисунке.
Задание 17
(№ 193090)
Подсказка

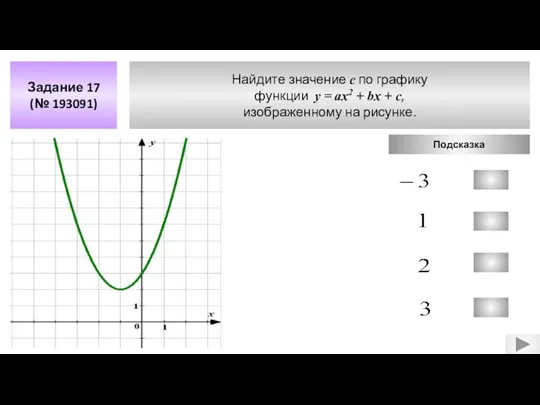
Найдите значение c по графику
функции у = aх2 + bx + c,
изображенному на рисунке.
Задание 17
(№ 193091)
Подсказка

функции у = aх2 + bx + c,

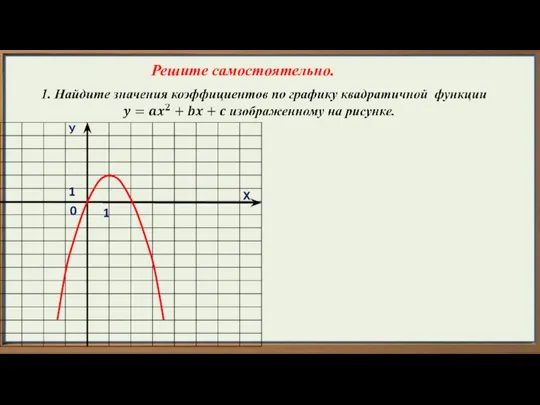
Х
У
1
1
0
Решите самостоятельно.

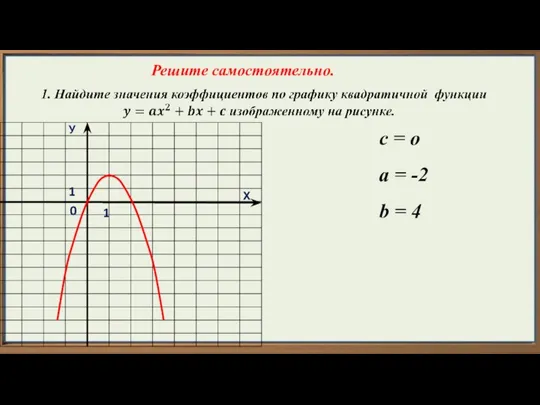
Х
У
1
1
0
с = о
а = -2
b = 4
Решите самостоятельно.