Содержание
- 2. Основная задача ЛП со смешенными ограничениями: Филиппова А.С., каф. ИТ, БГПУ
- 3. Математический аппарат задач ЛП Когда ограничения области допустимых решений в мат.модели задачи записаны в виде неравенств,
- 4. Пример. Филиппова А.С., каф. ИТ, БГПУ
- 5. Пример. Филиппова А.С., каф. ИТ, БГПУ
- 6. В матричном виде задача ЛП (ЗЛП): Филиппова А.С., каф. ИТ, БГПУ
- 7. Филиппова А.С., каф. ИТ, БГПУ
- 8. Филиппова А.С., каф. ИТ, БГПУ
- 9. Симплексный метод решения ЗЛП Используется математическое описание задачи в канонической форме и матричном виде Алгоритм состоит
- 10. Филиппова А.С., каф. ИТ, БГПУ
- 11. Филиппова А.С., каф. ИТ, БГПУ
- 12. Определение ответа задачи по симплекс таблице: каждому отрицательному коэффициенту в векторе решений C ставится в соответствие
- 13. Ведущим столбцом м.б. Назначен любой столбец t матрицы, удовлетворяющий одному из условий: Первый столбец, содержащий элемент
- 14. Ведущим столбцом м.б. Назначен любой столбец t матрицы, удовлетворяющий одному из условий: Первый столбец, содержащий элемент
- 15. Ведущим столбцом м.б. Назначен любой столбец t матрицы, удовлетворяющий одному из условий: Первый столбец, содержащий элемент
- 16. Филиппова А.С., каф. ИТ, БГПУ Замечание. Этот критерий для задач, целевая функция которых содержит только положительны
- 17. Филиппова А.С., каф. ИТ, БГПУ Пример.
- 18. Филиппова А.С., каф. ИТ, БГПУ Пример. Приведем к задаче канонического вида (добавим фиктивные переменные)
- 19. Филиппова А.С., каф. ИТ, БГПУ Пример. Приведем к задаче канонического вида (добавим фиктивные переменные)
- 20. Филиппова А.С., каф. ИТ, БГПУ Условие задачи в матричном виде:
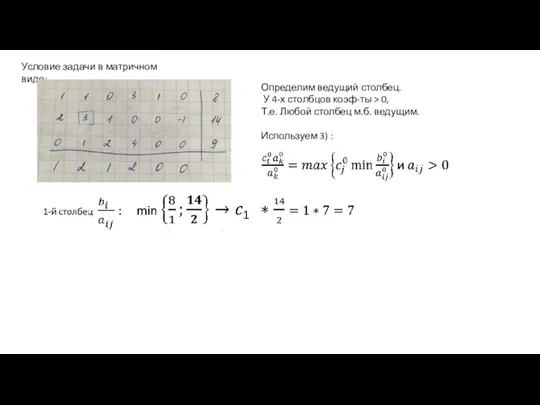
- 21. Филиппова А.С., каф. ИТ, БГПУ Условие задачи в матричном виде: Определим ведущий столбец. У 4-х столбцов
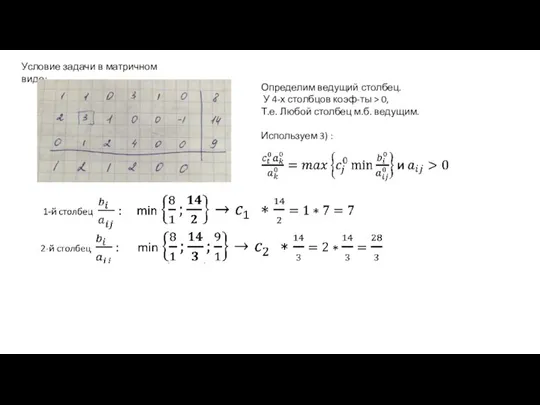
- 22. Филиппова А.С., каф. ИТ, БГПУ Условие задачи в матричном виде: Определим ведущий столбец. У 4-х столбцов
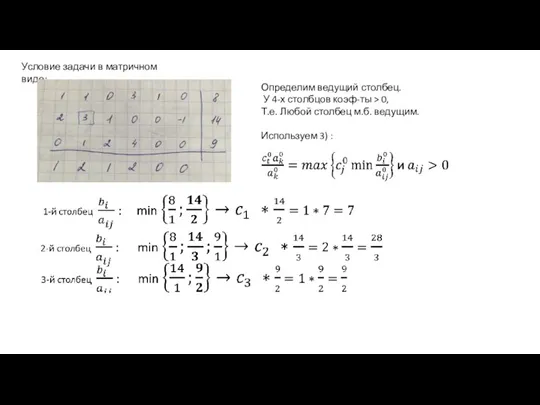
- 23. Филиппова А.С., каф. ИТ, БГПУ Условие задачи в матричном виде: Определим ведущий столбец. У 4-х столбцов
- 24. Филиппова А.С., каф. ИТ, БГПУ Условие задачи в матричном виде: Определим ведущий столбец. У 4-х столбцов
- 25. Филиппова А.С., каф. ИТ, БГПУ Условие задачи в матричном виде: Определим ведущий столбец. У 4-х столбцов
- 26. Филиппова А.С., каф. ИТ, БГПУ Условие задачи в матричном виде: Определим ведущий столбец. У 4-х столбцов
- 27. Филиппова А.С., каф. ИТ, БГПУ
- 28. Филиппова А.С., каф. ИТ, БГПУ В остальных строках матрицы коэффициент при второй переменной д.б. =0 Такое
- 29. Филиппова А.С., каф. ИТ, БГПУ
- 30. Филиппова А.С., каф. ИТ, БГПУ
- 31. Филиппова А.С., каф. ИТ, БГПУ Т.к. есть еще элементы вектора решений >0, то выполняем аналогичные шаги
- 32. Филиппова А.С., каф. ИТ, БГПУ Т.к. есть еще элементы вектора решений >0, то выполняем аналогичные шаги
- 33. Филиппова А.С., каф. ИТ, БГПУ Т.к. есть еще элементы вектора решений >0, то выполняем аналогичные шаги
- 34. Филиппова А.С., каф. ИТ, БГПУ Т.к. есть еще элементы вектора решений >0, то выполняем аналогичные шаги
- 35. Филиппова А.С., каф. ИТ, БГПУ Т.к. есть еще элементы вектора решений >0, то выполняем аналогичные шаги
- 36. Филиппова А.С., каф. ИТ, БГПУ
- 37. Филиппова А.С., каф. ИТ, БГПУ
- 38. Филиппова А.С., каф. ИТ, БГПУ
- 39. Филиппова А.С., каф. ИТ, БГПУ
- 40. Филиппова А.С., каф. ИТ, БГПУ Общий случай решения задач ЛП симплексным методом
- 41. Филиппова А.С., каф. ИТ, БГПУ 1) Мат.модель приводят ко 2-ой канонической форме, потом добавляют один шаг
- 42. Филиппова А.С., каф. ИТ, БГПУ Общий случай решения задач ЛП симплексным методом
- 44. Скачать презентацию






































 Действия с функциями (9 задание ЕГЭ)
Действия с функциями (9 задание ЕГЭ) Математическая модель игры World of Tanks
Математическая модель игры World of Tanks преобразование графиков (1)
преобразование графиков (1) Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика Элементы теории вероятностей
Элементы теории вероятностей predel_funktsii
predel_funktsii Симметрия в природе и в жизни
Симметрия в природе и в жизни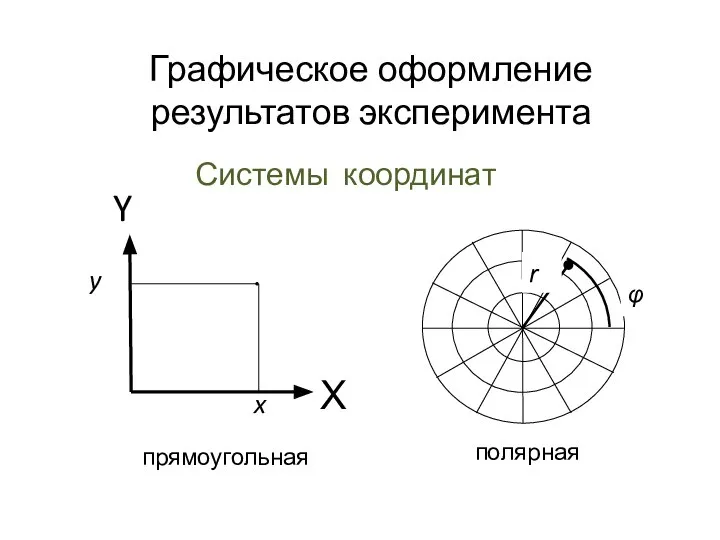 Графическое оформление результатов эксперимента
Графическое оформление результатов эксперимента Задачи. Геометрия 8 кл
Задачи. Геометрия 8 кл Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Стародубцева Анна 9-а класс
Стародубцева Анна 9-а класс Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Свойства квадратного корня
Свойства квадратного корня Подобие треугольников
Подобие треугольников Школа волшебников
Школа волшебников Сосчитай-ка, угадай-ка. 4 класс
Сосчитай-ка, угадай-ка. 4 класс Основные тригонометрические формулы
Основные тригонометрические формулы Определители
Определители Разные задачи. Способ Пропорция
Разные задачи. Способ Пропорция Алгебра. Дроби. Сумма дробей
Алгебра. Дроби. Сумма дробей Применение мультимедийных презентаций для организации устных упражнений на уроках математики в 5-6 классах. Модуль 1
Применение мультимедийных презентаций для организации устных упражнений на уроках математики в 5-6 классах. Модуль 1 Решение иррациональных уравнений
Решение иррациональных уравнений Тригонометрические уравнения. Арксинус
Тригонометрические уравнения. Арксинус Задание 7. Простейшие текстовые задачи
Задание 7. Простейшие текстовые задачи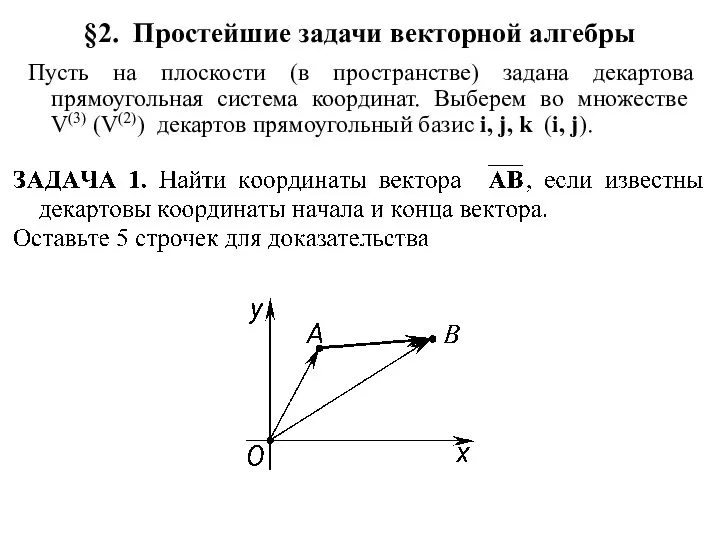 Простейшие задачи векторной алгебры
Простейшие задачи векторной алгебры Группировка слагаемых
Группировка слагаемых Урок математики 4 класс Тема: «Письменное умножение на числа, оканчивающиеся нулями» МБУО «Новообинцевская средняя общеобразова
Урок математики 4 класс Тема: «Письменное умножение на числа, оканчивающиеся нулями» МБУО «Новообинцевская средняя общеобразова Система географических координат
Система географических координат