Содержание
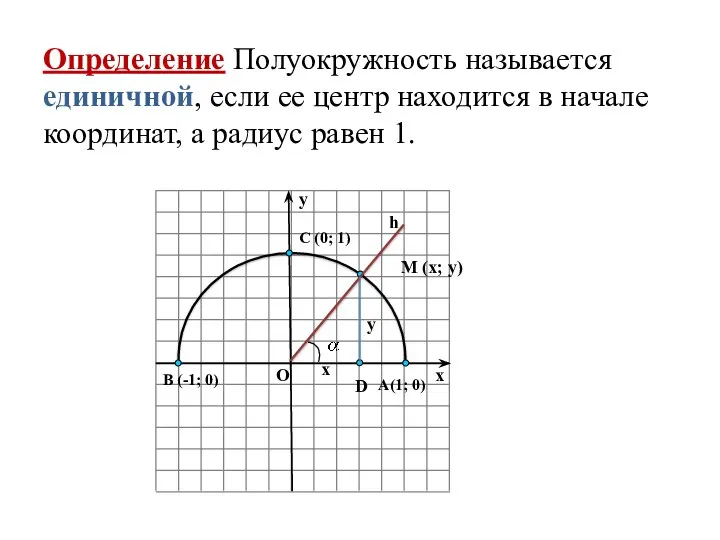
- 2. Определение Полуокружность называется единичной, если ее центр находится в начале координат, а радиус равен 1. M
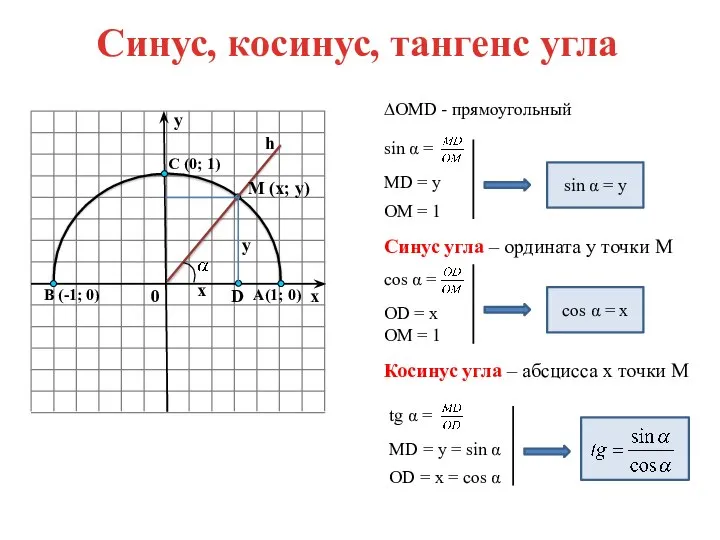
- 3. sin α = ∆OMD - прямоугольный MD = y OM = 1 sin α = y
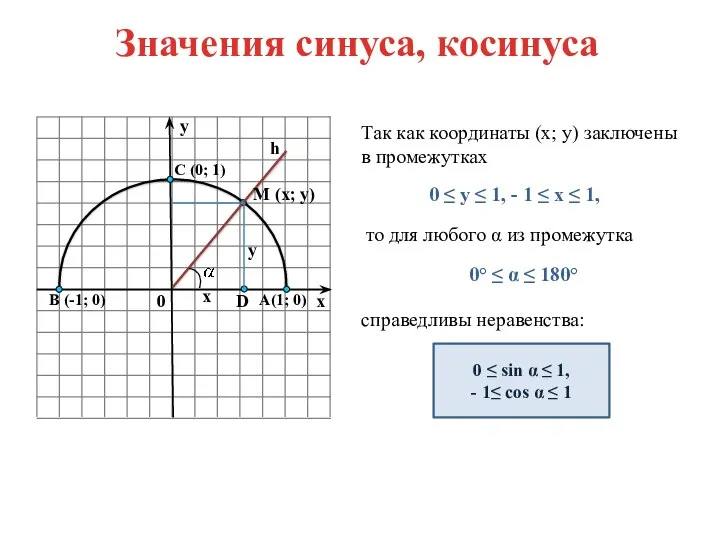
- 4. Значения синуса, косинуса Так как координаты (х; у) заключены в промежутках 0 ≤ у ≤ 1,
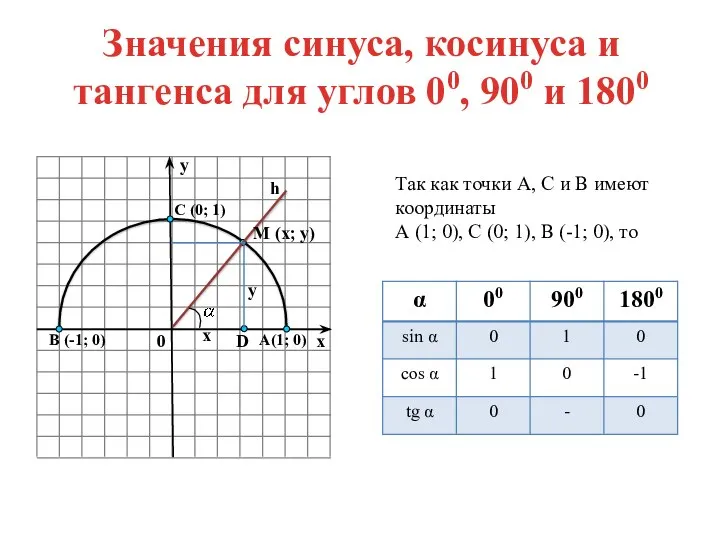
- 5. Значения синуса, косинуса и тангенса для углов 00, 900 и 1800 Так как точки А, С
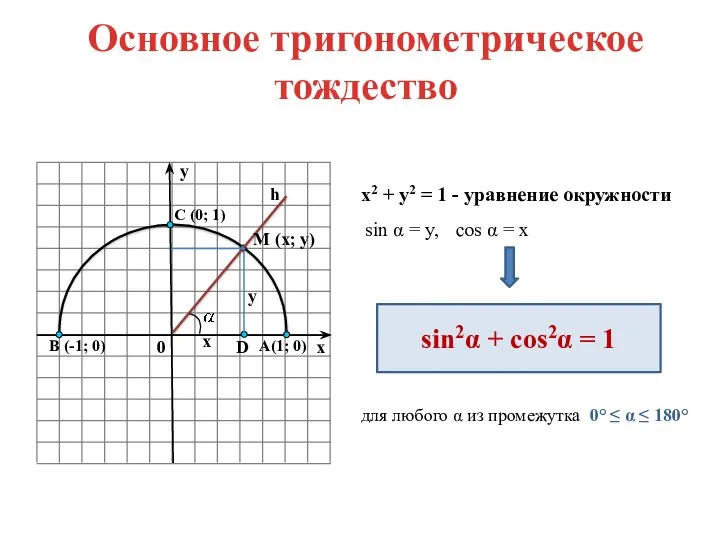
- 6. Основное тригонометрическое тождество х2 + у2 = 1 - уравнение окружности sin α = y, cos
- 7. Формулы приведения при 0° ≤ α ≤ 90° sin (90° - α) = cos α cos
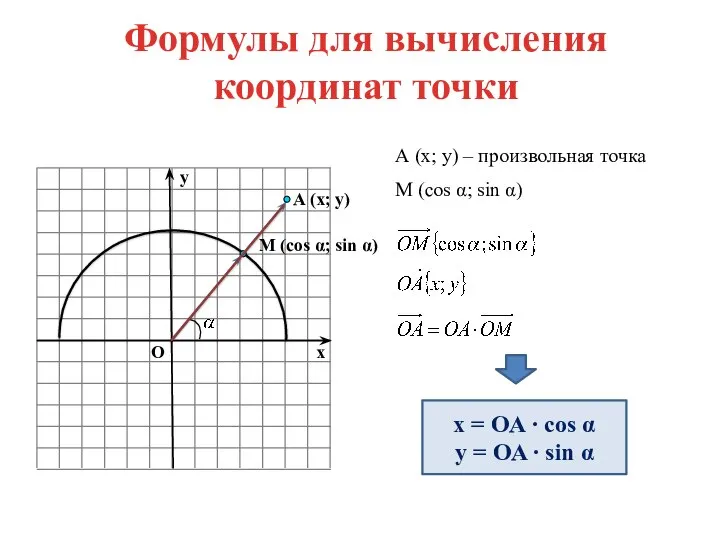
- 8. A (x; y) x y O M (cos α; sin α) Формулы для вычисления координат точки
- 10. Скачать презентацию

 Разбор заданий очного тура Олимпиады по математике
Разбор заданий очного тура Олимпиады по математике Непрерывный интервальный ряд распределения. Гистограмма
Непрерывный интервальный ряд распределения. Гистограмма Учение – это сила. Зимняя математическая олимпиада
Учение – это сила. Зимняя математическая олимпиада Площадь и объём фигуры
Площадь и объём фигуры Признаки и свойства параллельных прямых
Признаки и свойства параллельных прямых Виды треугольников по видам углов
Виды треугольников по видам углов Презентация на тему Признаки подобия треугольников
Презентация на тему Признаки подобия треугольников  Уравнение прямой
Уравнение прямой Qeyri stasionar qaz dinamikasi. Tənliyinin riyazi modelinin. Qurulmasi
Qeyri stasionar qaz dinamikasi. Tənliyinin riyazi modelinin. Qurulmasi Логарифм произведения двух функций
Логарифм произведения двух функций Представление о ломаной линии и многоугольнике
Представление о ломаной линии и многоугольнике Backpropagation
Backpropagation Презентация на тему Таблица умножения на 2 и 3
Презентация на тему Таблица умножения на 2 и 3  Преобразование обыкновенной дроби в десятичную
Преобразование обыкновенной дроби в десятичную Двойственные задачи линейного программирования. Лекция 3
Двойственные задачи линейного программирования. Лекция 3 Математика в профессии геодезиста
Математика в профессии геодезиста Построение графиков функций
Построение графиков функций Четырехугольники
Четырехугольники Практические задания на применение формул сокращённого умножения
Практические задания на применение формул сокращённого умножения Невыпуклый многогранник: Геометрическая фигура или плод человеческой фантазии? 11 класс
Невыпуклый многогранник: Геометрическая фигура или плод человеческой фантазии? 11 класс Правильные многогранники
Правильные многогранники Предел функции
Предел функции Способ группировки
Способ группировки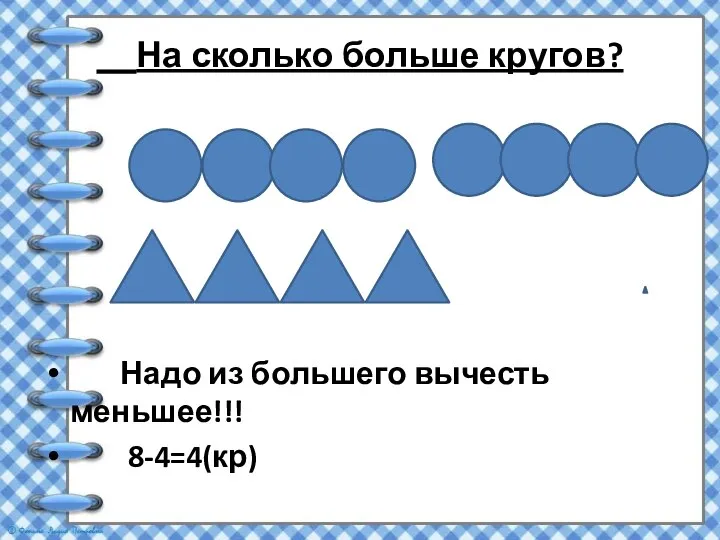 Вычетание
Вычетание Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Решение задач по теме: Двумерный массив. Профильный уровень
Решение задач по теме: Двумерный массив. Профильный уровень Презентация на тему Арифметические действия с числами
Презентация на тему Арифметические действия с числами