Содержание
- 2. §2. Числовые последовательности 1. Основные понятия ОПРЕДЕЛЕНИЕ 1. Последовательностью называется перенумерованное множество (чисел – числовая последовательность,
- 3. Принято обозначать: аргумент последовательности: n (или k) значения функции: xn, yn и т.д. Называют: x1 –
- 4. ОПРЕДЕЛЕНИЕ. Числовая последовательность { xn } называется ограниченной снизу, если ∃a∈ℝ такое, что a ≤ xn
- 5. 2. Предел последовательности ОПРЕДЕЛЕНИЕ. Число a∈ℝ называется пределом последовательности { xn } если ∀ε>0 ∃N∈ℕ такое,
- 6. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ предела последовательности Пусть r∈ℝ, M(r)∈Ox M(r) – геометрическая интерпретация числа r∈ℝ . Пусть x0∈ℝ,
- 7. Из определения предела последовательности получаем: если {xn}→a , то с геометрической точки зрения это означает, что
- 8. СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 1) Две последовательности, отличающиеся на конечное число членов, ведут себя одинаково относительно сходимости.
- 9. ОПРЕДЕЛЕНИЕ. Последовательность, сходящуюся к нулю, называют бесконечно малой. 5) ЛЕММА 1 (о роли б.м. последовательностей). Число
- 10. 6) Пусть {xn} – ограничена, {αn} – бесконечно малая. Тогда {xn ⋅ αn} – бесконечно малая.
- 11. СЛЕДСТВИЕ свойства 7. Если {xn} сходится к a, то ∀c∈ℝ последовательность {cxn} тоже сходится, причем Говорят:
- 12. 10) ЛЕММА о двух милиционерах. Пусть последовательности {xn} и {yn} сходятся к одному и тому же
- 14. Скачать презентацию











 Неравенства. Практическая работа №3
Неравенства. Практическая работа №3 Пропорции
Пропорции Преобразование функций и действия над ними
Преобразование функций и действия над ними Представление чисел с плавающей запятой
Представление чисел с плавающей запятой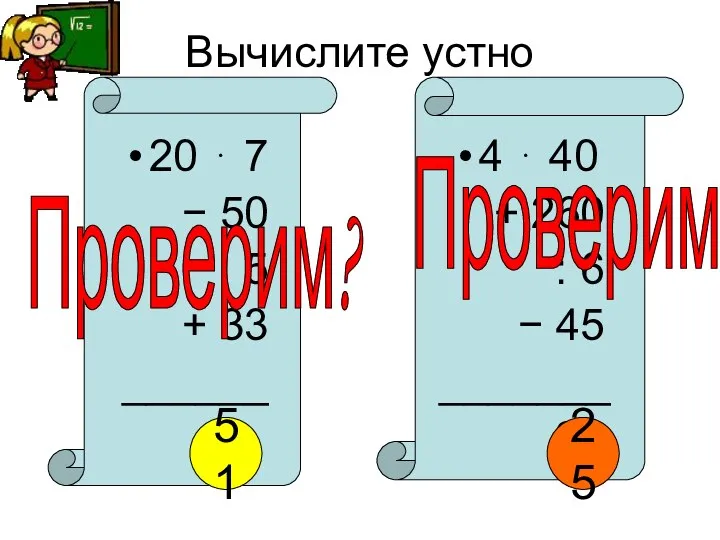 Вычислите устно. Задания
Вычислите устно. Задания Презентация на тему Такая разная геометрия
Презентация на тему Такая разная геометрия  Блиц-турнир по математике
Блиц-турнир по математике Случаи вычитания 12 -
Случаи вычитания 12 - Решение задач. 7 класс
Решение задач. 7 класс Число Пи вокруг нас
Число Пи вокруг нас Смежные и вертикальные углы
Смежные и вертикальные углы Решение систем уравнений графическим и аналитическим способом
Решение систем уравнений графическим и аналитическим способом chislo-pi
chislo-pi Икосаэдр
Икосаэдр Обыкновенные дроби
Обыкновенные дроби Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды Сложение и вычитание дробей
Сложение и вычитание дробей Дистанционный конкурс Царство ребусов
Дистанционный конкурс Царство ребусов Игры разума. Физико-математическая игра для учащихся 8 классов
Игры разума. Физико-математическая игра для учащихся 8 классов Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Презентация на тему Куб
Презентация на тему Куб  Абсолютная величина вектора в пространстве
Абсолютная величина вектора в пространстве Презентация на тему Доли. Обыкновенные дроби (5 класс)
Презентация на тему Доли. Обыкновенные дроби (5 класс)  Riešenie rovníc, ak je neznáma na oboch stranách rovnice
Riešenie rovníc, ak je neznáma na oboch stranách rovnice Понятие о проценте
Понятие о проценте Чему научились во 2 классе
Чему научились во 2 классе Теорема Пифагора
Теорема Пифагора Презентация на тему Дециметр (1 класс)
Презентация на тему Дециметр (1 класс)