Содержание
- 2. Методы решения нелинейных уравнений Метод половинного деления Метод хорд Метод касательных Метод секущих Метод простой итерации
- 3. Метод половинного деления (дихотомии) В качестве первого приближения берем Если f(x1)=0, то это корень, иначе переход
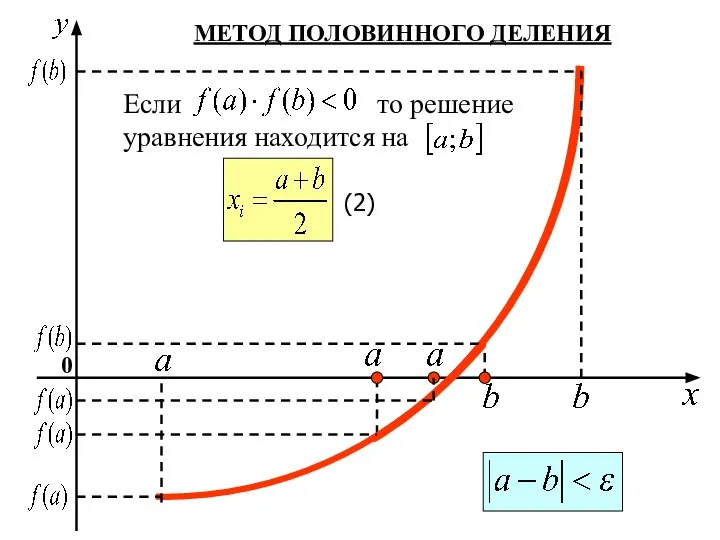
- 4. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ 0 Если то решение уравнения находится на (2)
- 5. Погрешность половинного деления На каждом шаге погрешность гарантированно уменьшается ровно вдвое. За n делений отрезок уменьшается
- 6. Можно априорно рассчитать по заданной погрешности количество шагов N(ε), необходимых для достижения точности ε:
- 7. Скорость сходимости метода половинного деления В данном методе выполняется условие: |x*-xi+1|≤ q |x*-xi| при q=½, т.е.
- 8. Особенности метода половинного деления Самый алгоритмически простой и надежный метод. Гарантированно сходится и скорость приближения не
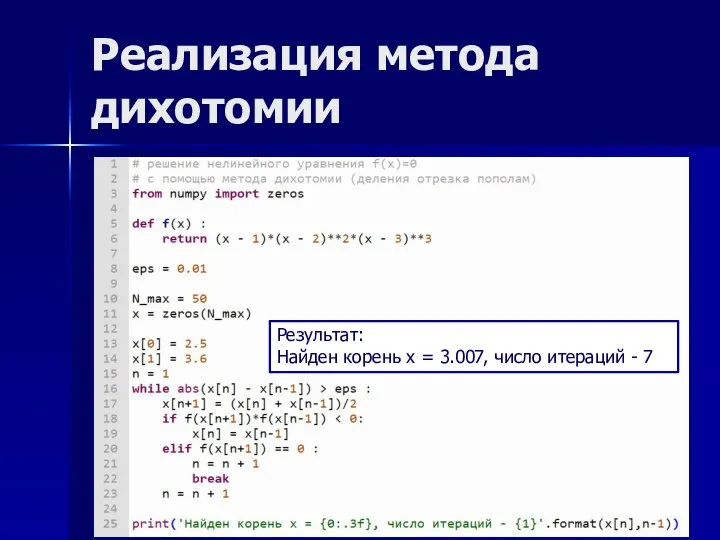
- 9. Реализация метода дихотомии Результат: Найден корень x = 3.007, число итераций - 7
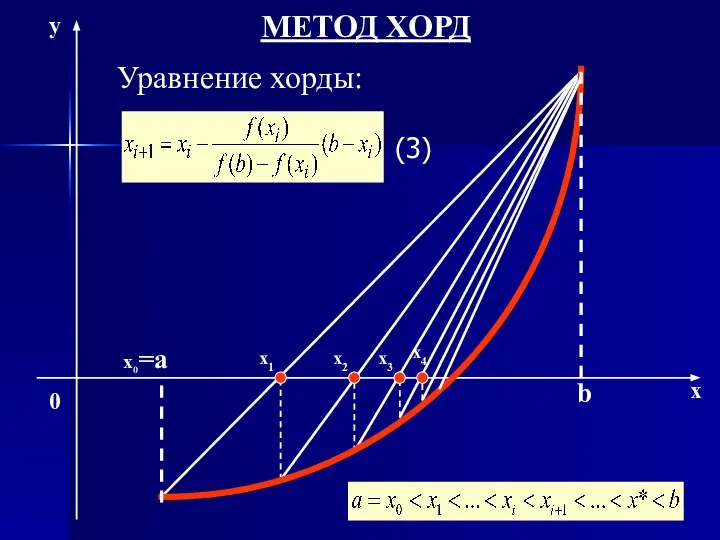
- 10. Метод хорд Идея метода основана на том, чтобы использовать не только разность знаков функции на концах
- 11. x0=а b x1 x2 x3 МЕТОД ХОРД x y 0 x4 Уравнение хорды: (3)
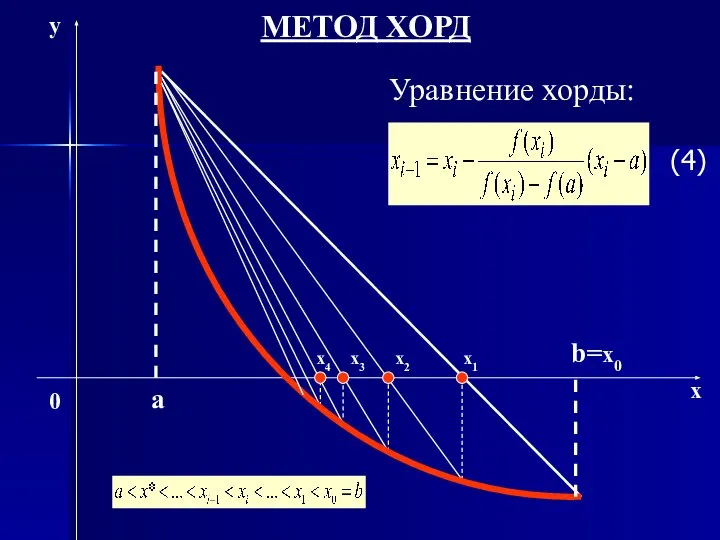
- 12. a b=x0 x1 x2 x3 МЕТОД ХОРД x y 0 x4 Уравнение хорды: (4)
- 13. Формулы метода хорд двигается левый конец интервала двигается правый конец интервала
- 14. Оценка погрешности
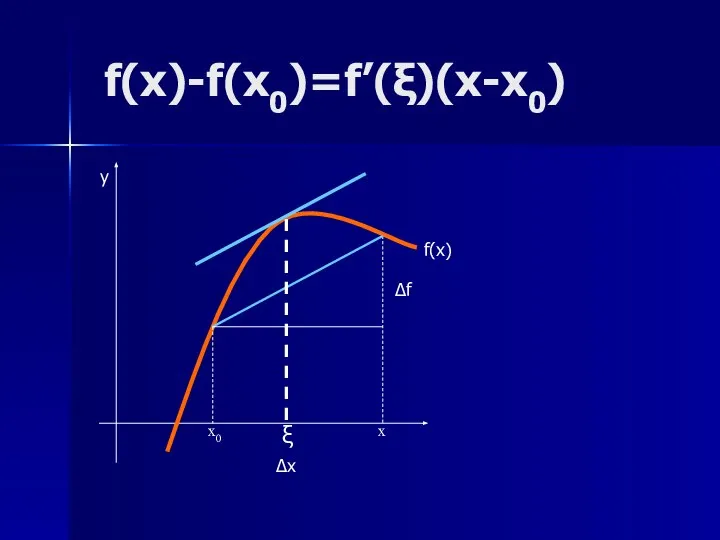
- 15. Оценка погрешности Теорема Лагранжа. Пусть функция f определена на некотором промежутке и имеет на нем конечную
- 16. f(x)-f(x0)=f’(ξ)(x-x0) x0 ξ x f(x) Δf y ∆x
- 17. Погрешность метода хорд Если f’ и f’’ непрерывны, а числа m и M такие, что тогда
- 18. Достижение точности Для условия достижения заданной точности можно воспользоваться оценкой (5): Однако, если интервал [a, b]
- 19. Особенности метода хорд Обычно сходиться быстрее, чем метод половинного деления. Не зависит от вида конкретной функции,
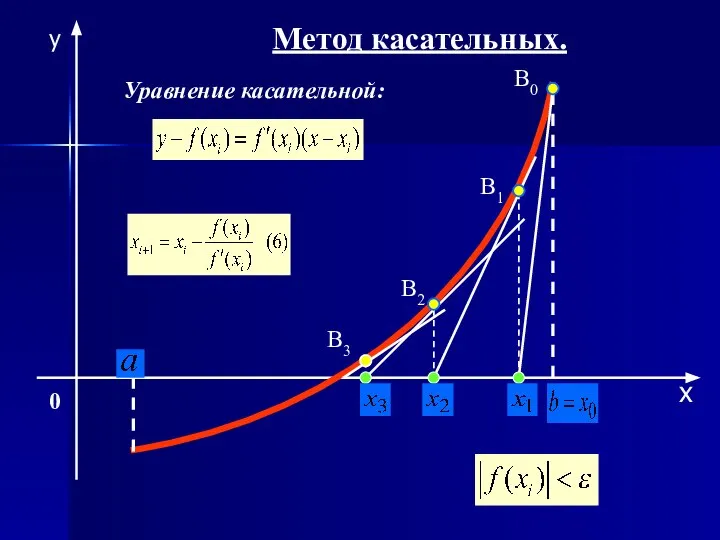
- 20. Метод касательных (метод Ньютона) Основная идея состоит в построении очередного приближения не хордой, а касательной к
- 21. 0 B0 B1 B2 B3 Метод касательных. Уравнение касательной: y x
- 22. Анализ сходимости метода Ньютона Формула Тейлора с остаточным членом в форме Лагранжа
- 23. Пусть x* - точный корень из [a;b], xn ≈ x*. Тогда между xn и x* найдётся
- 24. Оценка погрешности метода касательных Фактически в окрестности корня на каждой итерации погрешность возводиться в квадрат, т.е.
- 25. Достижение точности Для условия достижения заданной точности ε и прекращения вычислений можно использовать оценку (7):
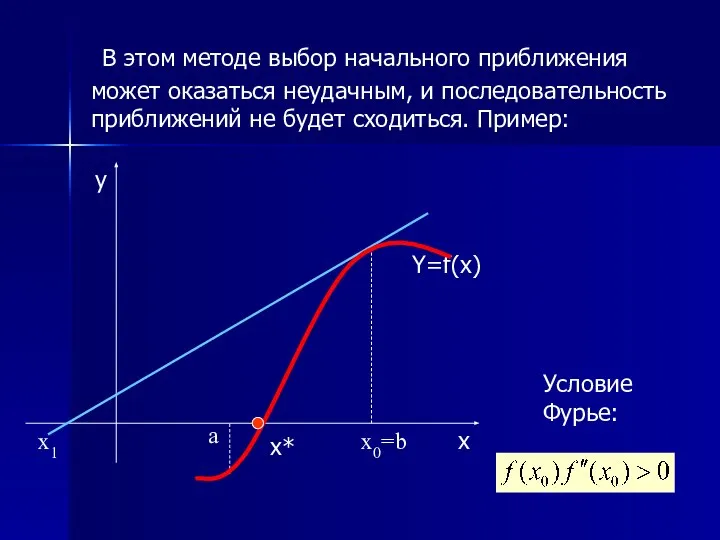
- 26. В этом методе выбор начального приближения может оказаться неудачным, и последовательность приближений не будет сходиться. Пример:
- 27. Особенности метода касательных Наиболее быстро сходящийся метод (квадратичная скорость сходимости). Необходимо вычислять в каждой точке приближения
- 28. Недостатки метода Ньютона можно преодолеть следующим образом: Для выхода в непосредственную близость корня сначала применяют гарантированный
- 29. Исторический пример использования метода Эмпирически метод касательных применялся в древности для нахождения квадратного корня (длины гипотенузы).
- 30. Пример Составим рекуррентное соотношение:
- 31. Пример: a=9
- 32. Метод секущих – это упрощение метода касательных, когда затруднительно найти производную. Заменим в методе касательных производную
- 33. Особенности метода секущих Не требует дифференцированной функции. При его реализации на каждой итерации вычисляется только одно
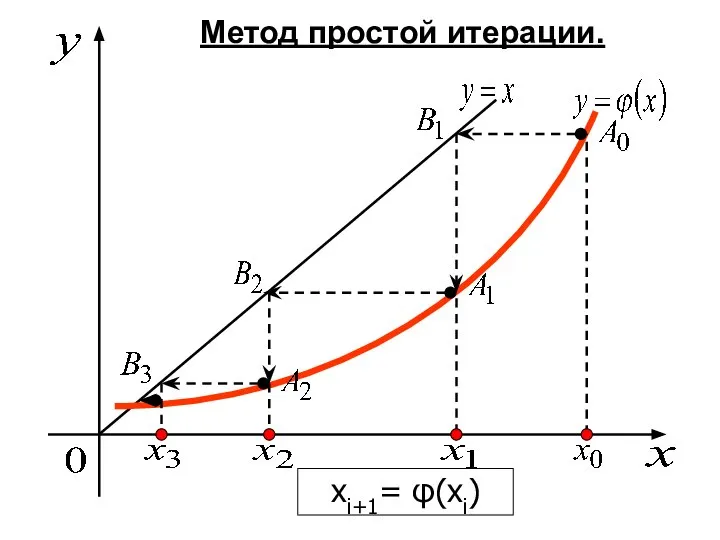
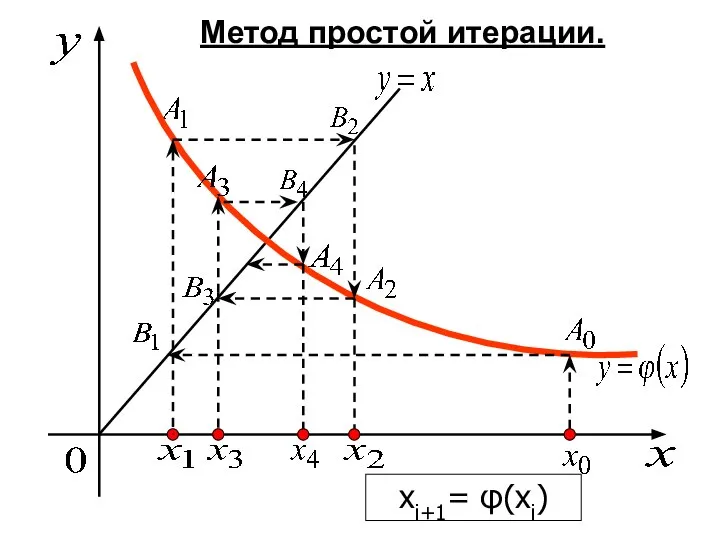
- 34. Метод простой итерации Рассмотренные методы решения уравнения f(x)=0 сводились к итерационной процедуре вида xi+1=φ(xi) (9) Основная
- 35. Исходное уравнение f(x)=0 заменяют эквивалентным ему x=φ(x). После этого выбирается начальное приближение x0, которое подставляют в
- 36. Метод простой итерации. xi+1= φ(xi)
- 37. Метод простой итерации. xi+1= φ(xi)
- 38. Таким образом, получим последовательность x0 ,x1 , x2 ,… , xi ,… Рассмотрим, в каком случае
- 39. Приведение уравнения к итерационному виду Пример 1. f(x)=0 x=φ(x)
- 40. Приведение уравнения к итерационному виду Пример 2. f(x)=0 x=φ(x)
- 41. Приведение уравнения к итерационному виду Способы приведения уравнения могут быть различными, но важно добиться выполнения условия
- 42. В общем случае используется следующий алгоритм: f(x)=0 умножим на константу λ λ*f(x)=0 вычтем обе части из
- 43. Пример. Пусть f(x)=x3-x2-1000=0. Это ур-е имеет один корень на [10,11]. Производная f’(x)=3x2-2x на [10,11] монотонно возрастает:
- 44. Подбор параметра λ Пусть на отрезке [a;b] производная функции f(x) ограничена: 0 Положим λ=2/(M1+ m1). Тогда
- 45. Упражнение. На отрезке [1;2] привести к итерационному виду уравнение x4-2x-3=0. Производная f’(x)=4x3-2 на [1;2] монотонно возрастает:
- 46. Оценка погрешности приближений Если то на каждой итерации
- 47. Условие достижения заданной точности Таким образом, если задана точность приближенного корня ε, то итерационный процесс необходимо
- 48. Особенности МПИ Самый простой в реализации. Скорость его сходимости зависит от конкретного вида (может быть линейной,
- 50. Скачать презентацию















![Пусть x* - точный корень из [a;b], xn ≈ x*. Тогда между](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1180647/slide-22.jpg)
















![Пример. Пусть f(x)=x3-x2-1000=0. Это ур-е имеет один корень на [10,11]. Производная f’(x)=3x2-2x](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1180647/slide-42.jpg)
![Подбор параметра λ Пусть на отрезке [a;b] производная функции f(x) ограничена: 0 Положим λ=2/(M1+ m1). Тогда](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1180647/slide-43.jpg)
![Упражнение. На отрезке [1;2] привести к итерационному виду уравнение x4-2x-3=0. Производная f’(x)=4x3-2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1180647/slide-44.jpg)



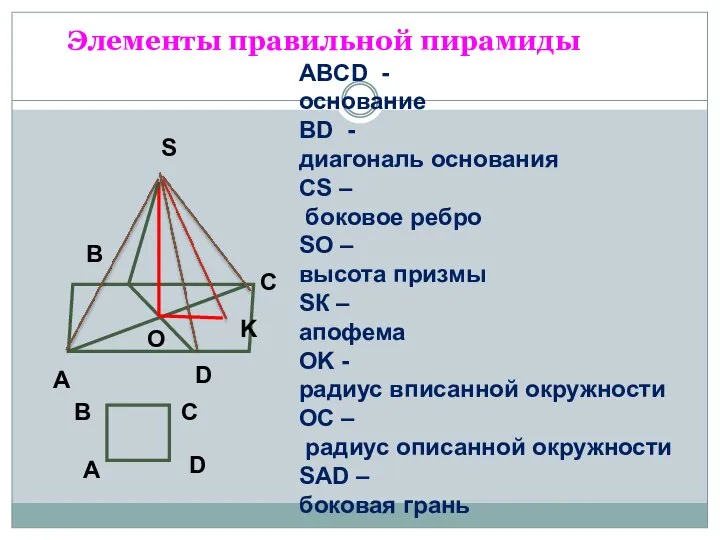 Правильная пирамида
Правильная пирамида Конфетное вычитание
Конфетное вычитание Решение задач на проценты
Решение задач на проценты Объёмные и плоские геометрические фигуры
Объёмные и плоские геометрические фигуры Осевая и центральная симметрии
Осевая и центральная симметрии Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Линейные уравнения и системы уравнений. Повторение
Линейные уравнения и системы уравнений. Повторение Турнир имени Лоповка
Турнир имени Лоповка Решение систем уравнений
Решение систем уравнений Призма. Площадь поверхности призмы. 10 класс
Призма. Площадь поверхности призмы. 10 класс Пчелки-труженицы. Примеры
Пчелки-труженицы. Примеры Многранники в нашей жизни
Многранники в нашей жизни Эндогенность. Инструментальные переменные
Эндогенность. Инструментальные переменные Сан. Числительное
Сан. Числительное Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число Преобразования графиков
Преобразования графиков Решение простейших тригонометрических уравнений. Подготовка к ЕГЭ
Решение простейших тригонометрических уравнений. Подготовка к ЕГЭ Уравнения, приводимые к квадратным
Уравнения, приводимые к квадратным Многочлен и его стандартный вид
Многочлен и его стандартный вид Решение задач на вычисление площади поверхности призмы
Решение задач на вычисление площади поверхности призмы Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Типы алгоритмов
Типы алгоритмов Сводка и группировка
Сводка и группировка Основы системной динамики
Основы системной динамики Устный счёт. 3 класс
Устный счёт. 3 класс Действия с числами, записанными в стандартном виде
Действия с числами, записанными в стандартном виде Группировка слагаемых. Сочетательное свойство сложения
Группировка слагаемых. Сочетательное свойство сложения Арифметическая прогрессия
Арифметическая прогрессия