Структура курса. Теория. Пакет Statistica

ИНТЕРПРЕТАЦИЯ ДАННЫХ
Корреляционный анализ
Простая регрессия
Множественная регрессия
Нелинейная регрессия
Дисперсионный анализ
Кластерный анализ
Дискриминантный анализ

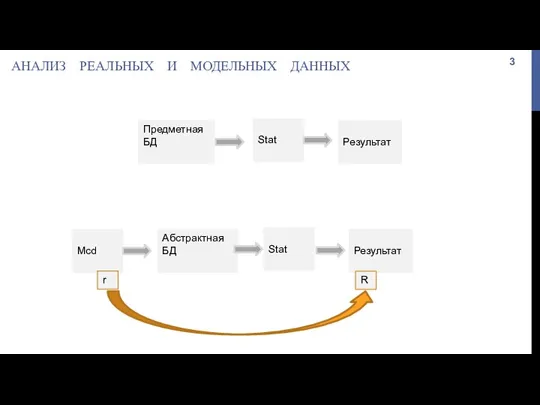
АНАЛИЗ РЕАЛЬНЫХ И МОДЕЛЬНЫХ ДАННЫХ
Предметная
БД
Stat
Результат
Абстрактная
БД
Stat
Результат
Mcd
r
R

МАТРИЧНЫЕ ОПЕРАЦИИ В MATHCAD
matrix(L,N,f) - создание матрицы - L – число строк, N – число столбцов, f - функция f(l,n)
identity(n) - создание единичной матрицы размерности n
diag(v) - создание диагональной матрицы с элементами главной диагонали из v;
geninv(А) - обращение матрицы А, аналогично операции А-1.
rows(А) - определение числа строк матрицы А
cols(А) - определение числа столбцов матрицы А
last(v) - вычисление номера последнего элемента вектора v
lenght(v) - вычисление количества элементов v
csort(А,i), rsort(А,j) - сортировка по возрастанию элементов i–го столбца или строки
min(А), max(А) - минимальный и максимальный элемент матрицы
tr(A) - след квадратной матрицы A
rank(A) - ранг матрицы A
norm1(A), norm2(A), norme(A), normi(A) - нормы квадратной матрицы A
submatrix (M, r1, r2, c1, c2) - подматрица М, r1 и r2 – нижний и верхний номер строки, с1 и с2 - нижней и верхний номер столбца матрицы М
augment(A,B,…), stack(A,B,…) - слияние матриц А, В, … слева направо или сверху вниз
rref(A) - приведение матрицы к ступенчатому виду с единичным базисным минором
eigenvals(A) - собственные значения квадратной матрицы А
eigenvecs(A) - собственные вектора квадратной матрицы А по порядку собственных значений
eigenvec(A, l) - собственный вектор для собственного значения
lsolve(A, b) - решение СЛАУ Ax=b

MATLAB

STATISTICA

СООТВЕТСТВИЕ ТЕРМИНОЛОГИИ

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Пространство элементарных событий
Любая природа
Не обязательно числовая
ξ≥0 ⇒ Mξ≥0;
Maξ=aMξ
M(ξ+η)=Mξ+Mη;
M(ξη)=MξMη - для независимых случайных величин
M(|ξη|)2≤MξMη - Неравенство Коши-Буняковского
Случайная величина –
числовая функция на пространстве элементарных событий
Числовые характеристики случайных величин
Математическое ожидание - Σxipi
Дисперсия - Dξ=M(ξ-Mξ)2
Ковариация - cov(ξ,η)=M(ξ-Mξ)(η-Mη)
Коэффициент корреляции
Dξ=Mξ2-(Mξ)2,
D(a+bξ)=b2 Dξ
cov(ξ,η)=M(ξη)-M(ξ)M(η)
Свойства математического ожидания Свойства дисперсии и ковариации

ИГРА В КОСТИ + ПЕТЕРБУРГСКИЙ ПАРАДОКС

СЛУЧАЙНЫЕ ВЕКТОРЫ
Математическое
ожидание
Дисперсионная матрица ξ - Dξ=||cov(ξi, ξj)||ij=1..n
Свойства Dξ: Dξ – симметрична (D=DT)
Dξ - неотрицательно-определенная (∀X: XTDX≥0)
D - дисперсионная матрица ⇒ D=ATA
Представление D: Dξ = M[(ξ-Mξ)(ξ-Mξ)T]
Некоторые доказательства
D=ATA ⇒ DT = (ATA)T = AT(AT)T = ATA = D
D=ATA ⇒ ∀X: XTDX = XT(ATA)X = (XTAT)(AX) = (AX)T(AX) = YTY = Σyi2 ≥0
Случайный вектор

ПРЕДСТАВЛЕНИЕ ДИСПЕРСИОННОЙ МАТРИЦЫ

МАТРИЧНАЯ АЛГЕБРА И НЕКОТОРЫЕ УТВЕРЖДЕНИЯ
C=A*B
(A*B)T = BT*AT
Линейное преобразование математического ожидания случайного вектора равно математическому ожиданию линейного преобразования В (Mξ) = M (Вξ)
ξ1
ξ3
ξ2
0
0.7
0.7
ξ1
ξ3
ξ2
0
1
1
Взаимные корреляции
Критерий неотрицательно определенной матрицы

ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ СЛУЧАЙНОГО ВЕКТОРА
- случайный вектор
A и B – числовые матрицы
Dξ=Dξ=||cov(ξi, ξj)||i,j=1..n - дисперсионная матрица ξ
Mξ=Mξ - математическое ожидание ξ
η=A+B ξ
Случайный вектор η представляет линейное преобразование вектора ξ
Задача: найти
Mη - математическое ожидание η
Dηη=Dη=||cov(ηi,ηj)||i,j=1…m
Утверждение
Mη=A+BMξ Dη=BDξBT
Mη = M(A+Вξ) = MA+M(Вξ) = A+В(Mξ)
Dη = M[(η-Mη)(η-Mη)T] = M[(A+Вξ-M(A+Вξ))(A+Вξ-M(A+Вξ))T] = M[(Вξ-MВξ)(Вξ-MВξ)T] = = M[В(ξ-Mξ)(В(ξ-Mξ))T] = M[В(ξ-Mξ)(ξ-Mξ)TВT] = ВM[(ξ-Mξ)(ξ-Mξ)T]ВT = ВDξВT.
Задан
вектор
ξ

ТЕОРЕМА О НОРМАЛЬНОЙ КОРРЕЛЯЦИИ
Оптимальное оценивание нормально-распределенных случайных векторов
Совместный случайный вектор
Минимизация суммы квадратов
- математическое ожидание совместного вектора
- дисперсионная матрица совместного вектора
Утверждение
Оценка вектора η
Ошибка оценка вектора η

ТЕОРЕМА О НОРМАЛЬНОЙ КОРРЕЛЯЦИИ (ДОКАЗАТЕЛЬСТВО)
Доказать
Вывод: ξ и ζ некоррелированы ⇒ в силу нормальности распределения - независимы
Оптимальная оценка ζ по ξ это Mζ=0 - 1-ое утверждение доказано
ξ1
ξ2
η
η|ξ
ζ
Доказать

ВЫВОД ФОРМУЛ ТЕОРЕМЫ О НОРМАЛЬНОЙ КОРРЕЛЯЦИИ

СЛУЧАЙ НЕЗАВИСИМЫХ ПРЕДИКТОРОВ И СКАЛЯРНОЙ ПРОГНОЗИРУЕМОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
(n+1)-мерный гауссовский вектор, причем ξ1, ξ2 … ξn попарно независимы
cov(ξi, ξj)=0, а η является одномерной величиной,

НАЗВАНИЕ СЛАЙДА

НАЗВАНИЕ СЛАЙДА

MATHCAD
- определение размеров матрицы
Xn- ввод нижнего индекса
x-1 - вычисление обратной матрицы
|x| - определитель матрицы |M|=detM или длина вектора |x|
→- поэлементные операции с матрицами
M<> - M
j-й столбец матрицы
MT - транспонирование матрицы
û⋅ê - скалярное произведение векторов x*y=Σxiyi
û×ê - векторное произведение a×b=(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1);
Σx - сумма компонент вектора Σx=Σxi
m..n - диапазон изменения переменной