Содержание
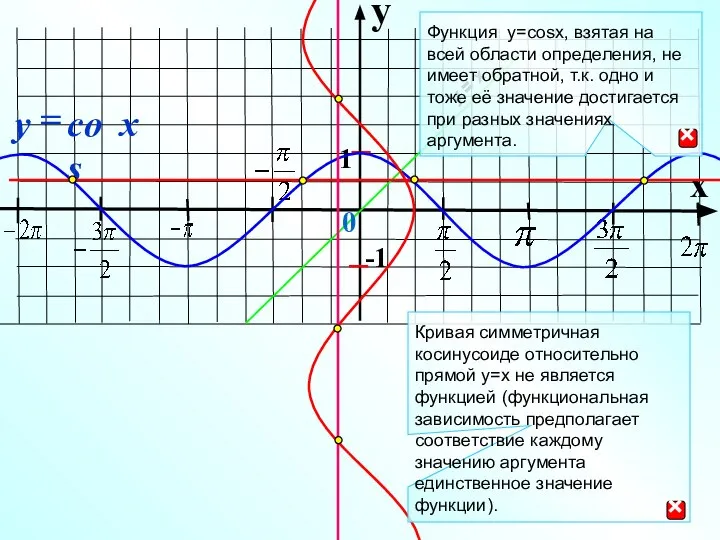
- 2. y x 1 -1 0 Функция y=cosx, взятая на всей области определения, не имеет обратной, т.к.
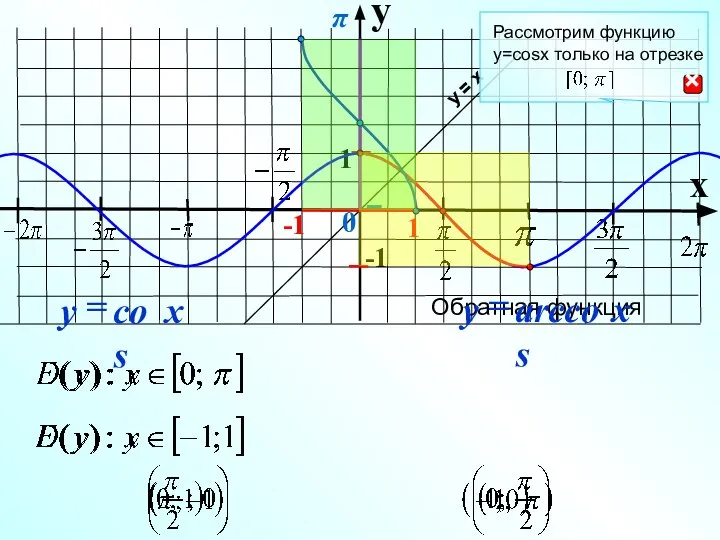
- 3. Обратная функция y x 1 -1 0 Рассмотрим функцию y=cosx только на отрезке
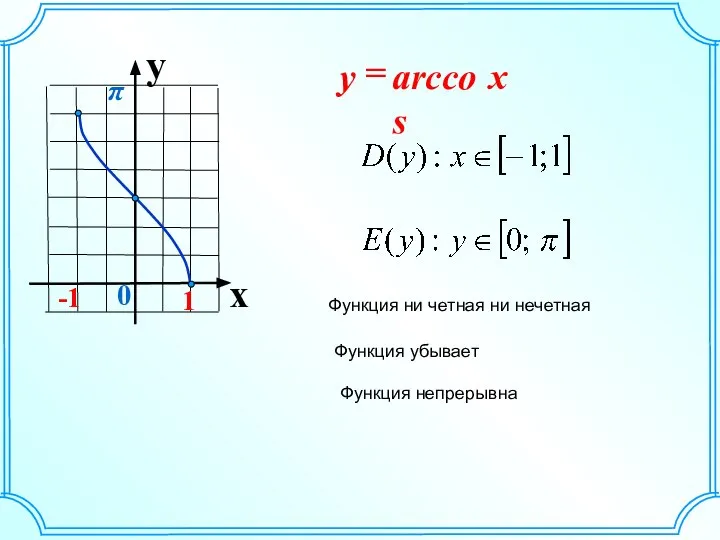
- 4. y x 0 -1 1 Функция ни четная ни нечетная Функция убывает Функция непрерывна
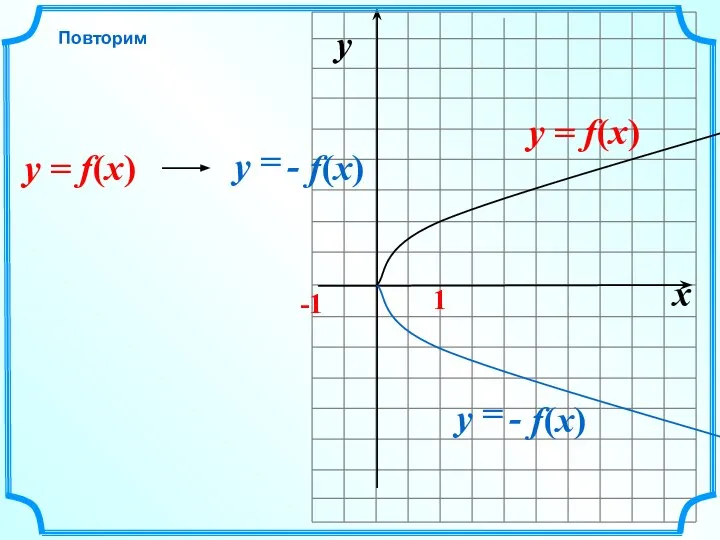
- 5. x y -1 1 Повторим
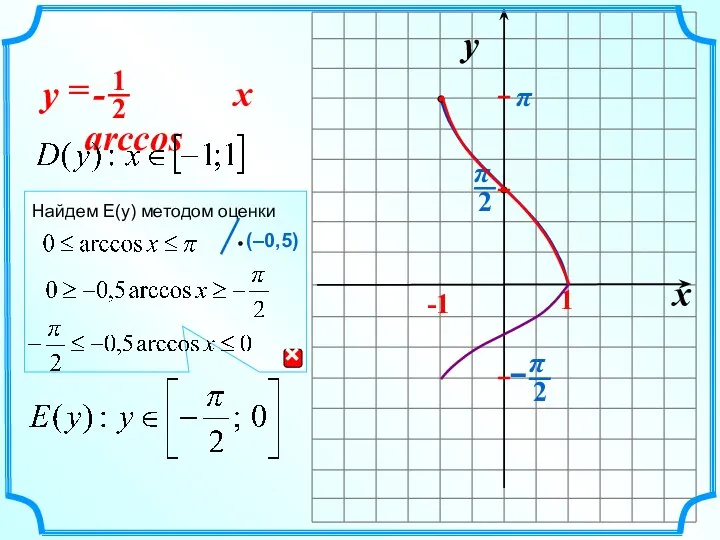
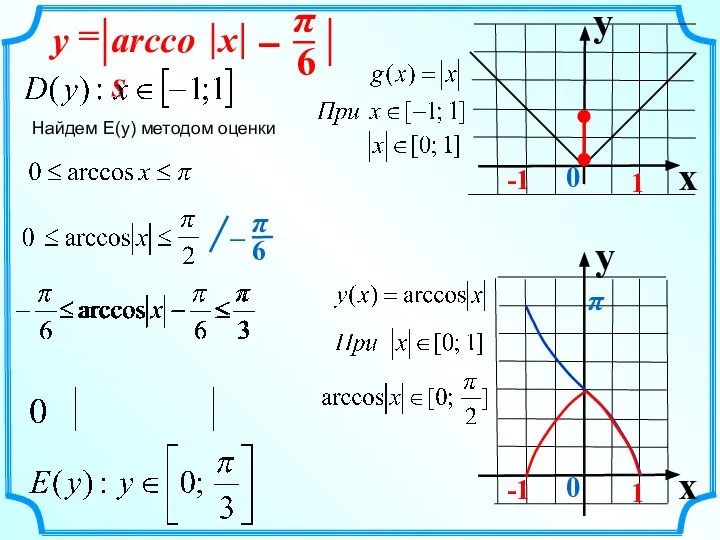
- 6. x y -1 1 - arccos = x y π Найдем E(y) методом оценки
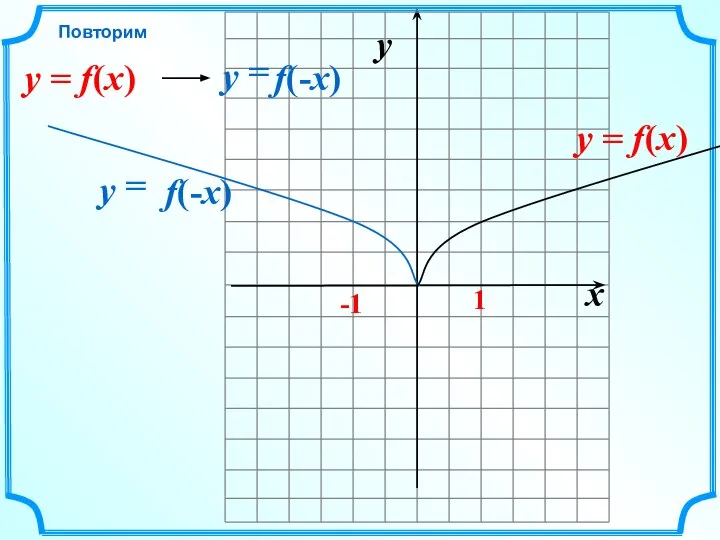
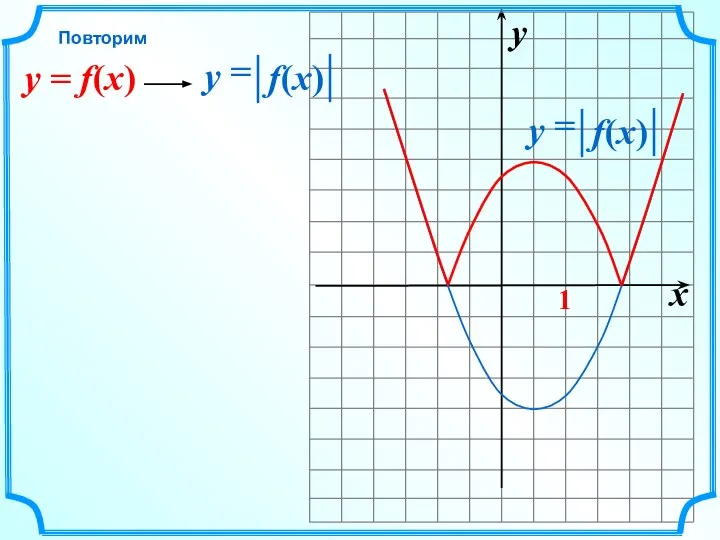
- 7. x y -1 1 = f(-x) y Повторим
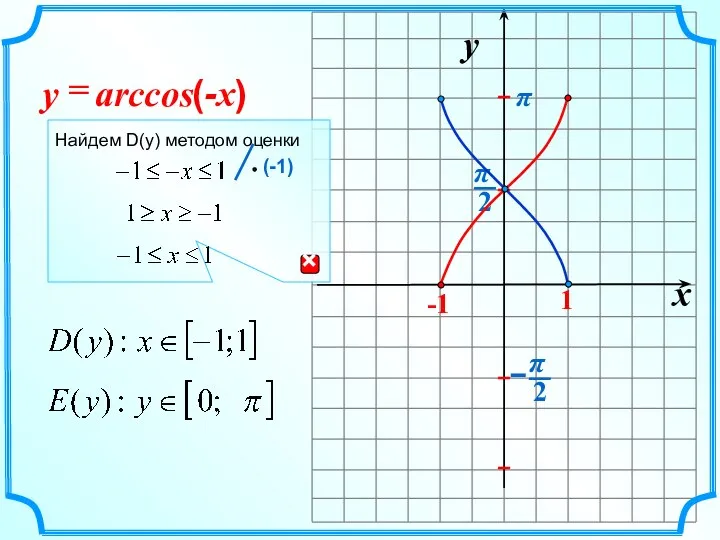
- 8. x y -1 1 arccos = (-x) y π Найдем D(y) методом оценки
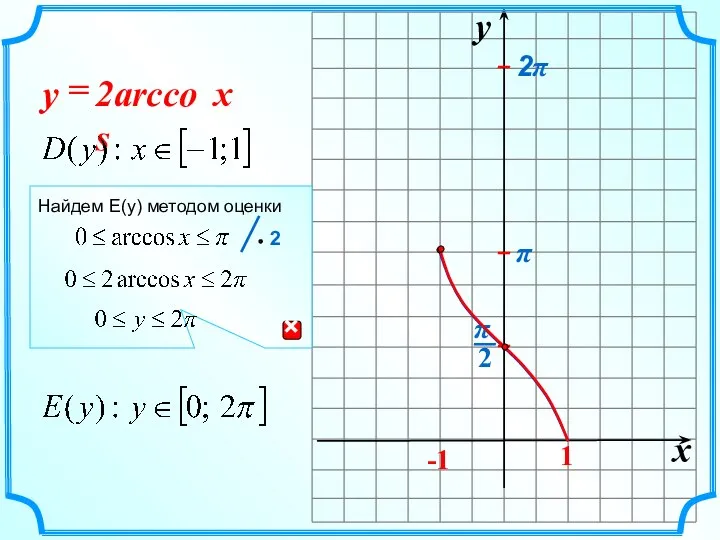
- 9. x y -1 1 2arccos = x y 2π π Найдем E(y) методом оценки
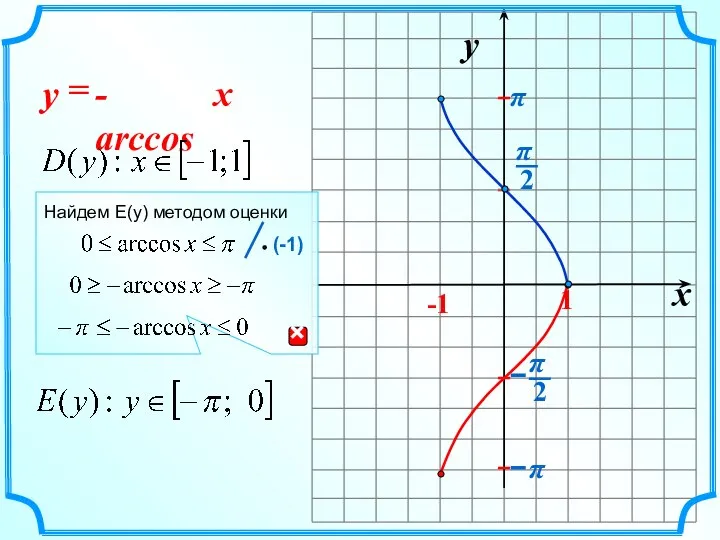
- 10. x y -1 1 - arccos = x y π Найдем E(y) методом оценки
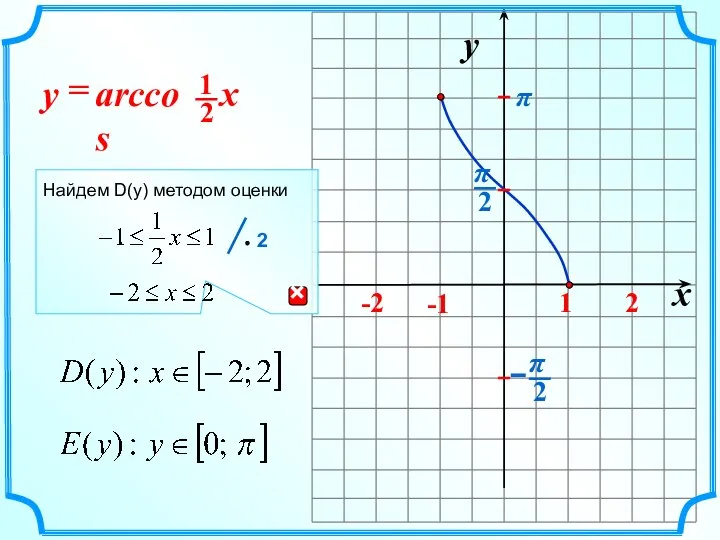
- 11. x y -1 1 arccos = x y π Найдем D(y) методом оценки
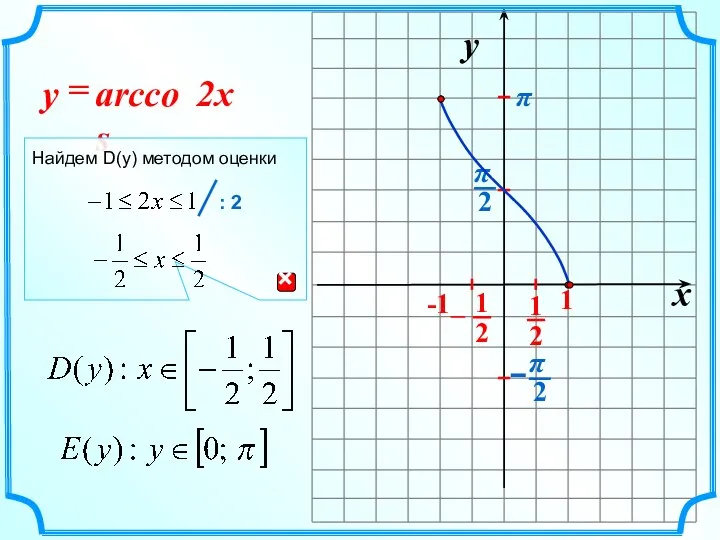
- 12. x y -1 1 arccos = 2x y π Найдем D(y) методом оценки
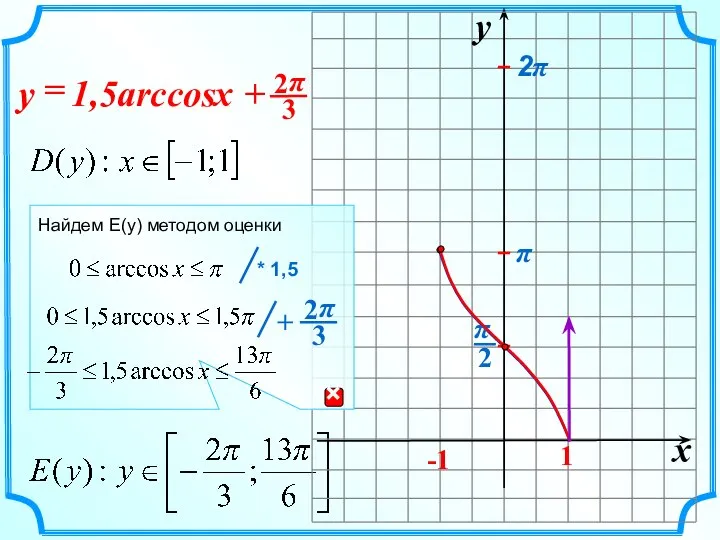
- 13. 1,5arccos + = x y x y -1 1 2π π Найдем E(y) методом оценки
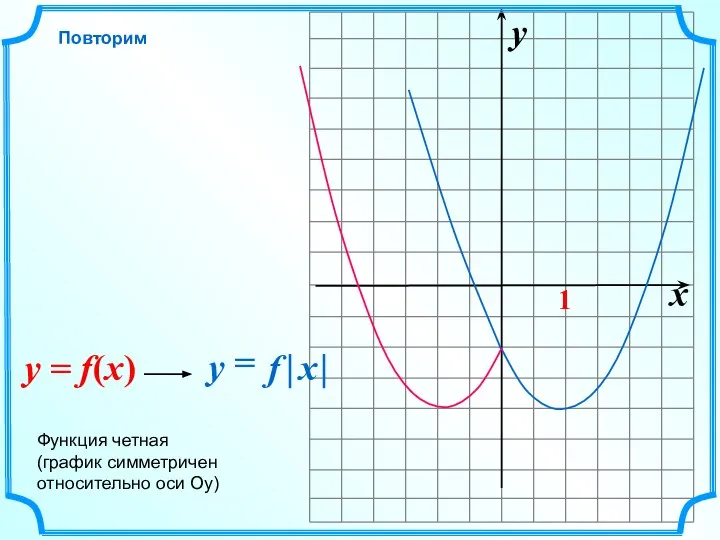
- 14. x y 1 Повторим
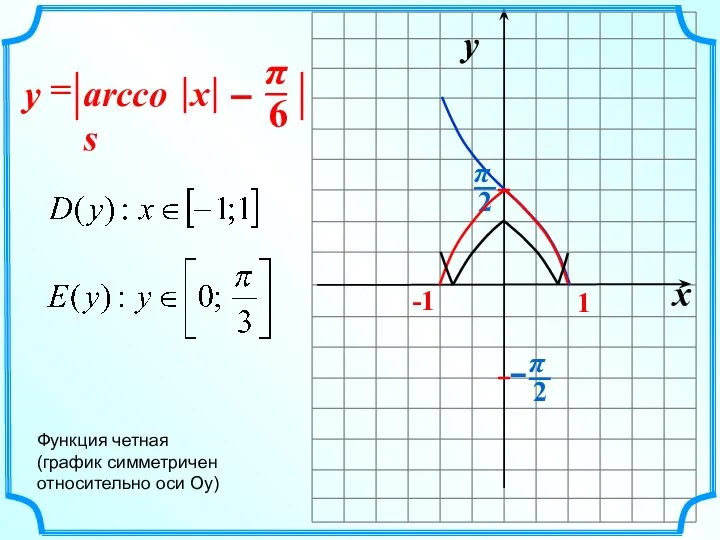
- 15. x y 1 Повторим Функция четная (график симметричен относительно оси Оу)
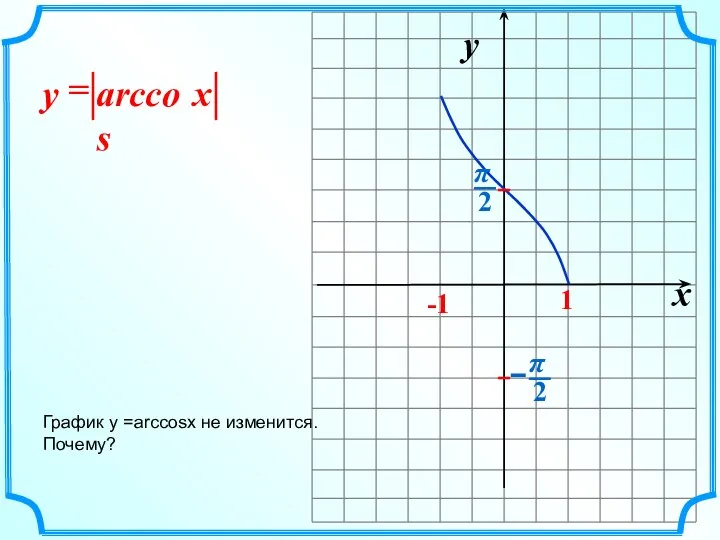
- 16. x y -1 1 arccos = x y График y =arccosx не изменится. Почему?
- 17. Найдем E(y) методом оценки arccos = x y
- 18. x y -1 1 arccos = x y Функция четная (график симметричен относительно оси Оу)
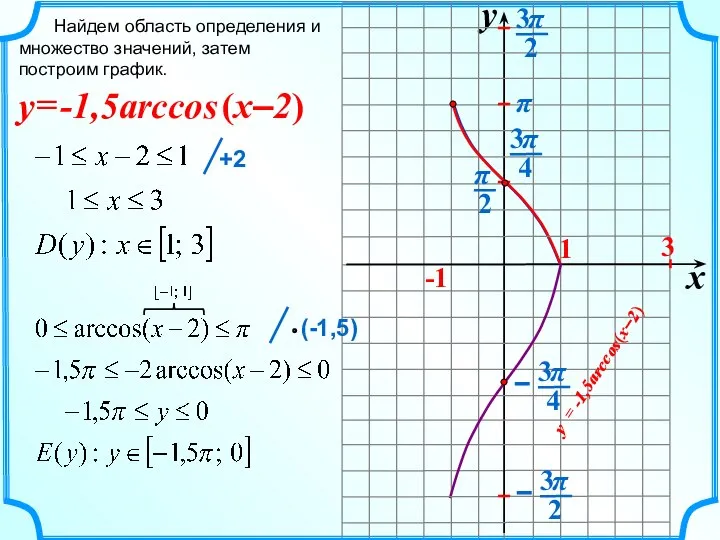
- 19. Найдем область определения и множество значений, затем построим график. -1,5arccos = (x–2) y y x -1
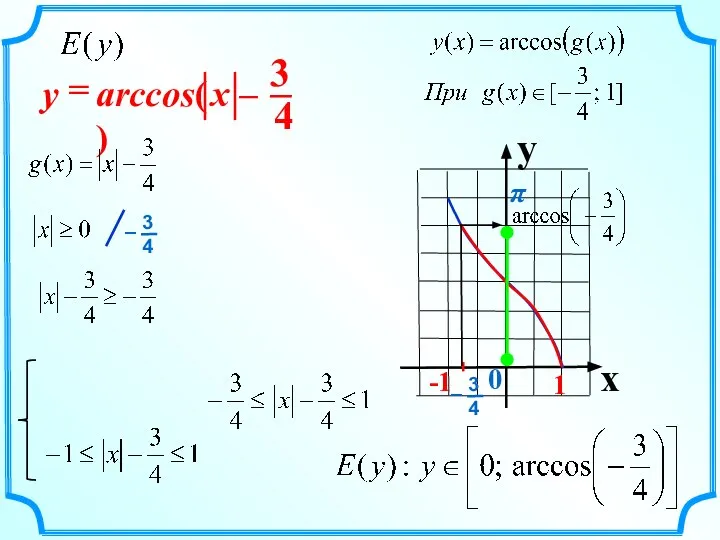
- 20. arccos( ) = x – y
- 21. arccos( ) = x – y
- 23. Скачать презентацию

 Алгоритм фронта волны
Алгоритм фронта волны Знакомство с монетами достоинством 1, 2, 5, 10 рублей
Знакомство с монетами достоинством 1, 2, 5, 10 рублей Тригонометрия на ЕГЭ. Профиль (1)
Тригонометрия на ЕГЭ. Профиль (1) Призма. Построение сечений призмы плоскостями
Призма. Построение сечений призмы плоскостями Формула у=х2
Формула у=х2 Действия с рациональными числами
Действия с рациональными числами Гипотеза Пуанкаре́
Гипотеза Пуанкаре́ Система MatLab. Методические указания к выполнению лабораторных работ
Система MatLab. Методические указания к выполнению лабораторных работ Презентация на тему Вычисление производной
Презентация на тему Вычисление производной  Периметр и площадь прямоугольника
Периметр и площадь прямоугольника Виды треугольников. 3 класс
Виды треугольников. 3 класс Счет от 0 до 20
Счет от 0 до 20 Квадратные уравнения. Повторение. 8 класс
Квадратные уравнения. Повторение. 8 класс Круги Эйлера. Геометрические фигуры
Круги Эйлера. Геометрические фигуры Пропорциональность величин
Пропорциональность величин Презентация на тему Окружность, ее центр и радиус
Презентация на тему Окружность, ее центр и радиус  Піраміда
Піраміда Задачи на проценты. ОГЭ
Задачи на проценты. ОГЭ Метод Зейделя
Метод Зейделя Действительный анализ. Теорема Лебега (примеры). Измеримые множества
Действительный анализ. Теорема Лебега (примеры). Измеримые множества РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4)
РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4) Очень жадный крокодил или больше, меньше, равно
Очень жадный крокодил или больше, меньше, равно Оптические свойства кривых второго порядка
Оптические свойства кривых второго порядка Решение примеров вида 12-1
Решение примеров вида 12-1 Преобразование графиков
Преобразование графиков Показательные уравнения и неравенства
Показательные уравнения и неравенства Пример проектирования цифрового устройства
Пример проектирования цифрового устройства Знакомство с линейкой
Знакомство с линейкой