Содержание
- 2. Сложение и вычитание многочленов
- 3. Что сделано дома Вхождение в тему урока и создание условий для осознанного восприятия нового материала. ?
- 4. Самостоятельная работа Проверка полученных результатов. Коррекция 1 вариант а,г 2 вариант б,в
- 5. Сложение и вычитание многочленов Организация и самоорганизация учащихся. Организация обратной связи Если перед числом поставить знак
- 6. Сложение и вычитание многочленов Организация и самоорганизация учащихся. Организация обратной связи Сумму и разность многочленов с
- 7. Отрабатываем алгоритм Практикум a – a – b б – m + n a – a
- 8. Отрабатываем алгоритм Практикум ? 1 P – Q + R = m2 + 2m – 2;
- 9. Домашнее задание П.7.2 № 661(в, е), 663(б), 664(б),
- 11. Скачать презентацию








 Задачи к уроку по теме Параллелограмм, 8 класс
Задачи к уроку по теме Параллелограмм, 8 класс ЕГЭ. Экономические задачи IV
ЕГЭ. Экономические задачи IV Геометрический материал
Геометрический материал Задачи на подобие треугольников
Задачи на подобие треугольников Геометрический смысл производной. Уравнение касательной
Геометрический смысл производной. Уравнение касательной Производная функции, заданной параметрически
Производная функции, заданной параметрически Счет до 10
Счет до 10 Алгебраические уравнения
Алгебраические уравнения Графики функций. Задания
Графики функций. Задания 0братная функция
0братная функция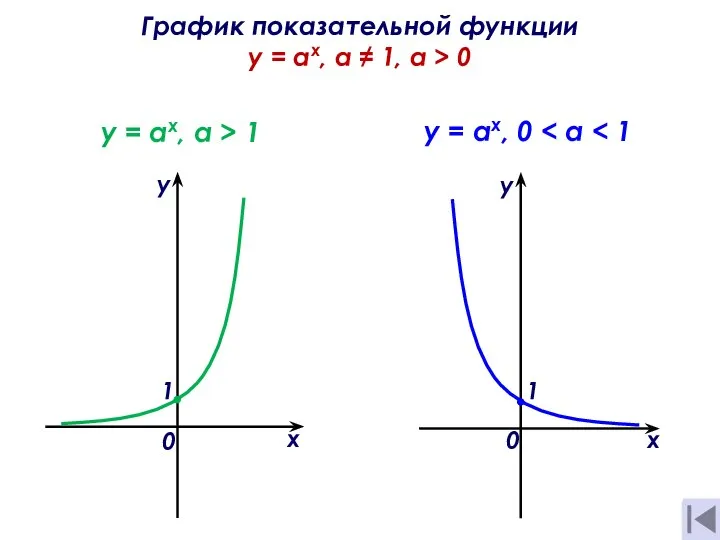 Показательные неравенства и уравнения
Показательные неравенства и уравнения Площадь треугольника и подобие
Площадь треугольника и подобие Классическое определение вероятности
Классическое определение вероятности Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс)  Аттестационная работа. Доли. Обыкновенные дроби. (5 класс)
Аттестационная работа. Доли. Обыкновенные дроби. (5 класс) Математика вокруг нас. Геометрия на столе с ножницами и без
Математика вокруг нас. Геометрия на столе с ножницами и без Решение неравенств
Решение неравенств Презентация на тему Диаграммы (6 класс)
Презентация на тему Диаграммы (6 класс)  Квадрат и куб
Квадрат и куб Многогранники. Призма
Многогранники. Призма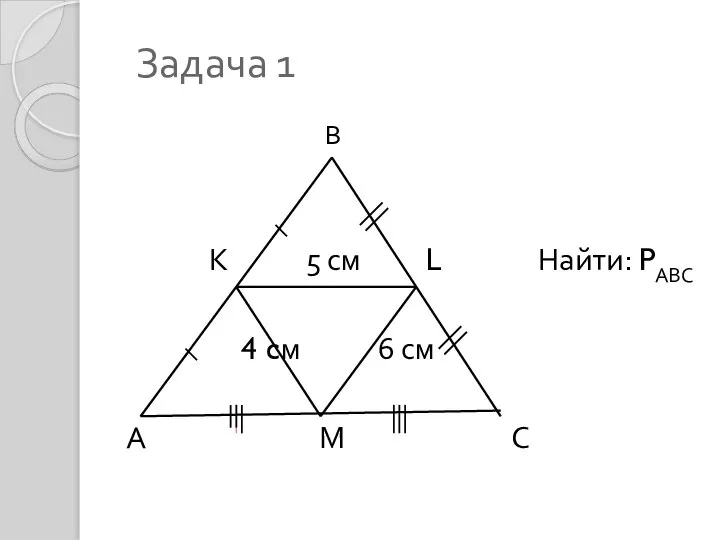 Средняя линия треугольника
Средняя линия треугольника Пропозиційна логика (продовження). Лекція №2
Пропозиційна логика (продовження). Лекція №2 Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости Ккомбинаторика. Перестановки. Размещения. Сочетания
Ккомбинаторика. Перестановки. Размещения. Сочетания Действия над матрицами. Обратная матрица. Лекция 2а
Действия над матрицами. Обратная матрица. Лекция 2а Принципы системного подхода к формированию систем статистических показателей
Принципы системного подхода к формированию систем статистических показателей Корреляция случайных величин
Корреляция случайных величин Дифференциальные уравнения 1 порядка
Дифференциальные уравнения 1 порядка