Содержание
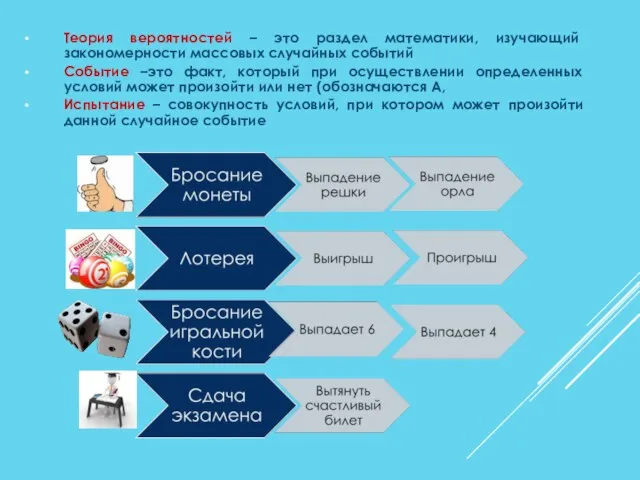
- 2. Теория вероятностей – это раздел математики, изучающий закономерности массовых случайных событий Событие –это факт, который при
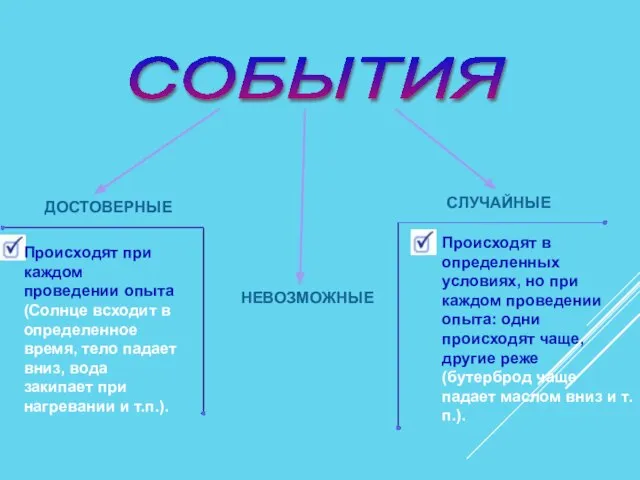
- 3. СОБЫТИЯ ДОСТОВЕРНЫЕ СЛУЧАЙНЫЕ Происходят при каждом проведении опыта (Солнце всходит в определенное время, тело падает вниз,
- 4. СОБЫТИЯ Совместные Несовместные Если в результате данного испытания появление одного из них не исключает появление (при
- 5. События образуют полную группу событий, если в результате испытания обязательно произойдет хотя бы одно из них
- 6. Два несовместных события называются противоположными, если в результате испытания одной из них должно обязательно произойти (обозначается
- 7. В толковом словаре С.И. Ожегова и Н.Ю. Шведовой: «Вероятность – возможность исполнения, осуществимости чего-нибудь». Основатель современной
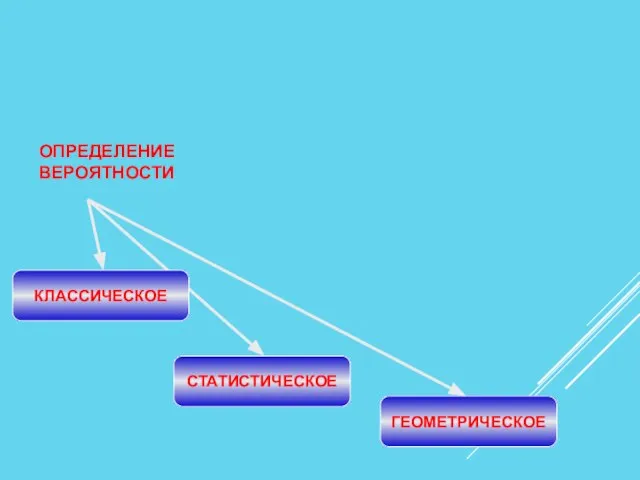
- 8. КЛАССИЧЕСКОЕ СТАТИСТИЧЕСКОЕ ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
- 9. ВЕРОЯТНОСТЬ – ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ. ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО
- 10. Пьер-Симо́н Лапла́с Классическое определение вероятности было впервые дано в работах французского математика Лапласа.
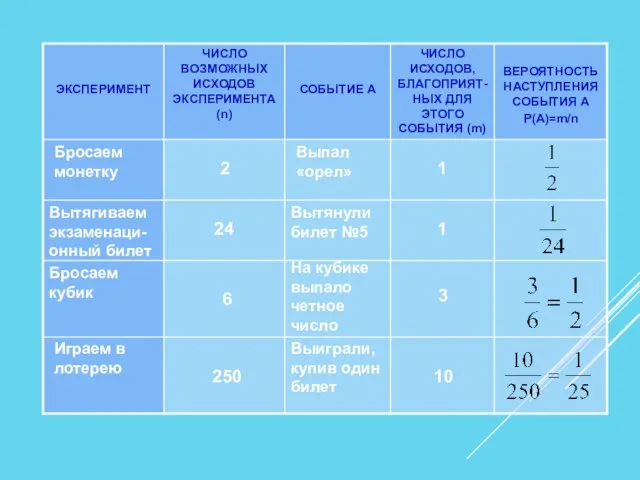
- 11. Бросаем монетку 2 Выпал «орел» 1 Вытягиваем экзаменаци- онный билет Вытянули билет №5 24 1 Бросаем
- 12. ПРИМЕР 1 В школе 1300 человек, из них 5 человек хулиганы. Какова вероятность того, что один
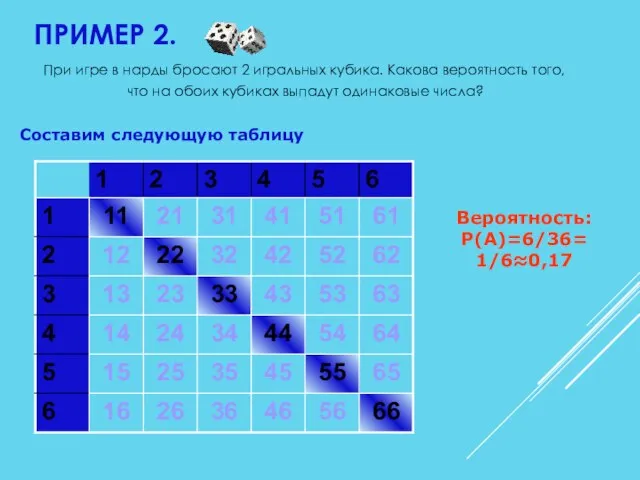
- 13. Составим следующую таблицу Вероятность: P(A)=6/36= 1/6≈0,17 При игре в нарды бросают 2 игральных кубика. Какова вероятность
- 14. Вероятность достоверного события равна P(А) = 1 Вероятность невозможного события равна P(А) = 0 Вероятность события
- 15. Задача 1. В коробке 4 синих, 3 белых и 2 желтых фишки. Они тщательно перемешиваются, и
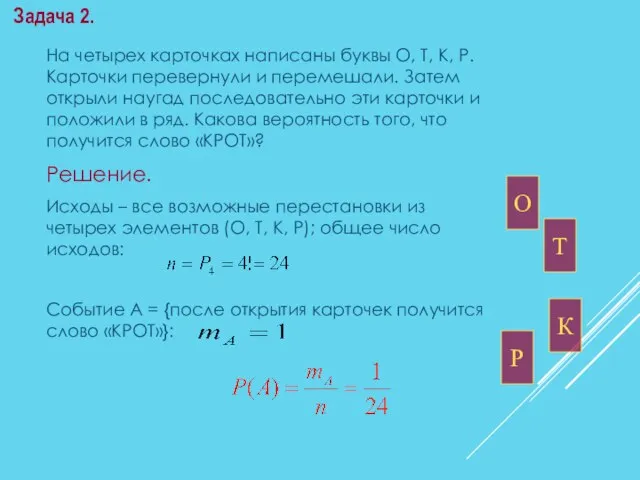
- 16. На четырех карточках написаны буквы О, Т, К, Р. Карточки перевернули и перемешали. Затем открыли наугад
- 17. Суммой событий А и В называют событие, которое наступает в том случае, когда происходит или событие
- 18. Теорема 1. Вероятность суммы двух событий равна сумме вероятностей этих событий, уменьшенной на вероятность произведения этих
- 19. Найти вероятность выпадения 2 или 3 при бросании игральной кости. Событие А – выпадение цифры 2,
- 21. Скачать презентацию












 Числовые неравенства и их свойства. Подготовка к ОГЭ
Числовые неравенства и их свойства. Подготовка к ОГЭ Функциональная зависимость
Функциональная зависимость Координаты вектора
Координаты вектора Перетворення подібності. Гомотерапія
Перетворення подібності. Гомотерапія Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Разложение правильной рациональной дроби на сумму простейших дробей. Лекция 2.2
Разложение правильной рациональной дроби на сумму простейших дробей. Лекция 2.2 Решаем задачи и уравнения
Решаем задачи и уравнения Решение задач на проценты. 6 класс. Урок 1
Решение задач на проценты. 6 класс. Урок 1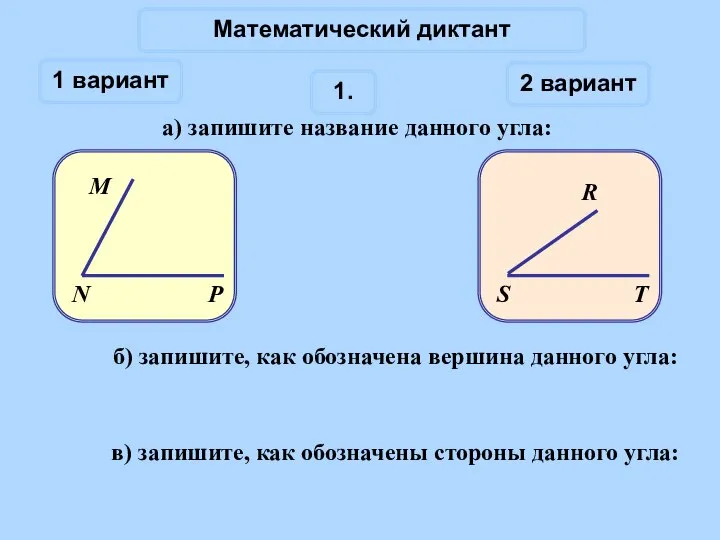 Углы. Математический диктант
Углы. Математический диктант Площади многоугольников
Площади многоугольников Древняя Индия
Древняя Индия Арифметические операции над матрицами
Арифметические операции над матрицами округление натуральных чисел 5 класс презентация
округление натуральных чисел 5 класс презентация Презентация на тему Математика 3 класс Виды треугольников
Презентация на тему Математика 3 класс Виды треугольников  Геометрический и механический смысл производной
Геометрический и механический смысл производной Решение задач с использованием теоремы о накрест лежащих углах
Решение задач с использованием теоремы о накрест лежащих углах Степенные функции, их свойства и графики
Степенные функции, их свойства и графики Вписанный угол
Вписанный угол Решение задач и примеров на сложение в пределах 1000 с переходом через разряд
Решение задач и примеров на сложение в пределах 1000 с переходом через разряд Числа 1 - 4. (1 класс)
Числа 1 - 4. (1 класс) Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Сфера и шар. 11 класс
Сфера и шар. 11 класс Геометрия на каждом уроке
Геометрия на каждом уроке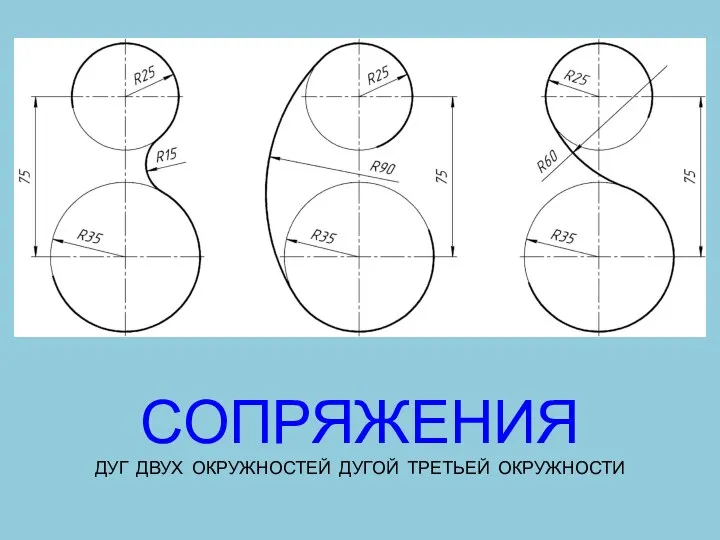 Сопряжения окружностей
Сопряжения окружностей Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Сложение смешанных дробей
Сложение смешанных дробей Статистика. Занятие 2
Статистика. Занятие 2 Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.
Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.