Содержание
- 2. А В С Какая запись является верной? 450
- 3. Назовите коллинеарные сонаправленные векторы Назовите коллинеарные противоположнонаправленные векторы Назовите равные векторы
- 4. Сложение векторов. Правило треугольника. b А В С ! ! Для любого нулевого вектора справедливо равенство
- 5. В1 Докажем, что если при сложении векторов точку А заменить другой точкой А1, то полученный вектор
- 6. Правило треугольника. RR = 0
- 7. Правило треугольника. АС = OB = RA = KX = AD = FO =
- 8. По правилу треугольника складываются и коллинеарные векторы, хотя при их сложении треугольника и не получается
- 10. Законы сложения векторов Для любых векторов справедливы равенства: 1 2 ! ! Теорема
- 11. А В D C
- 12. При доказательстве свойства 10 мы обосновали правило параллелограмма сложения неколлинеарных векторов. Чтобы применить правило параллелограмма, надо
- 13. Сложение векторов. Правило параллелограмма.
- 14. В D C Докажем свойство 2 А
- 15. Сложение векторов. Правило многоугольника.
- 16. Правило многоугольника можно сформулировать также следующим образом: если А1, А2, …, Аn – произвольные точки плоскости,
- 18. Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены.
- 19. № 766 На рисунке изображены векторы ХУ. Представьте вектор ХУ в виде суммы остальных или им
- 20. Вычитание векторов.
- 21. Вычитание векторов.
- 22. № 768 Точки М и N – середины сторон АВ и АС треугольника АВС. Выразите векторы
- 23. ( ) Найдите ABCD - прямоугольник А B C D АВ + AD – DC –
- 25. Скачать презентацию
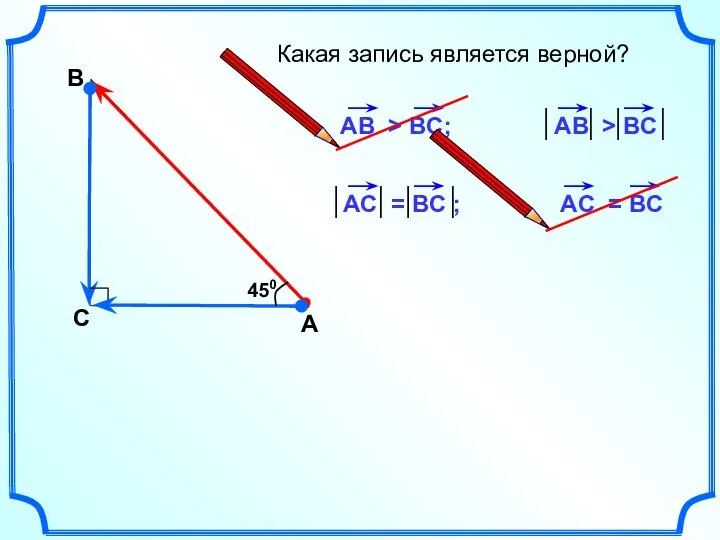
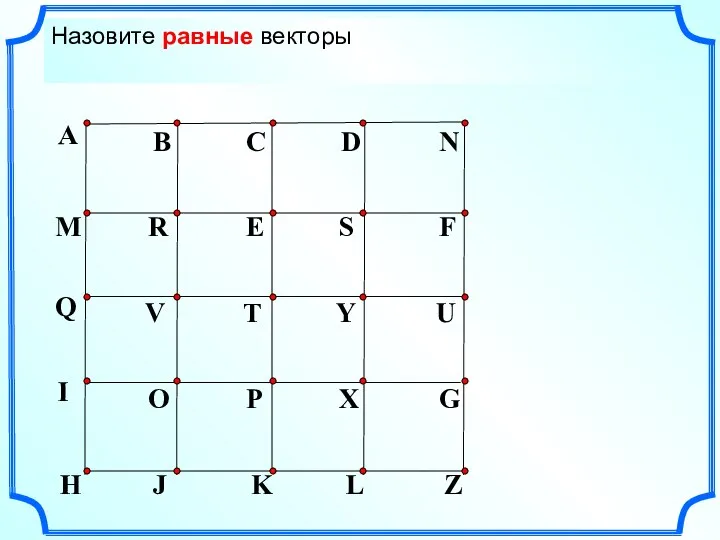
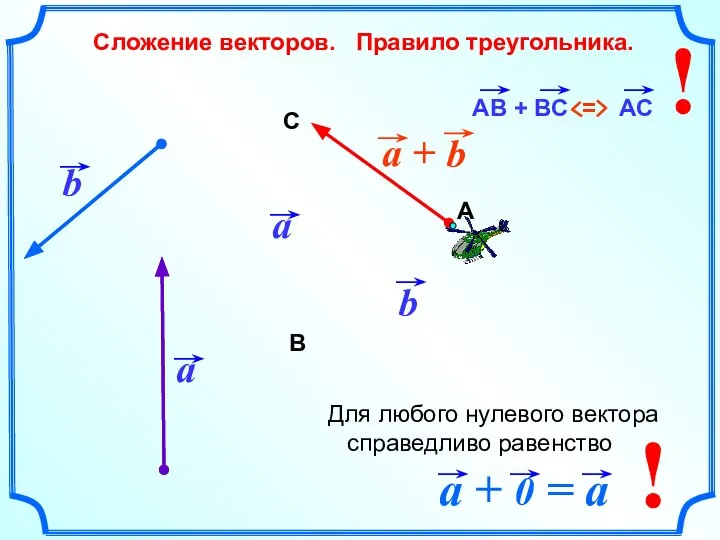
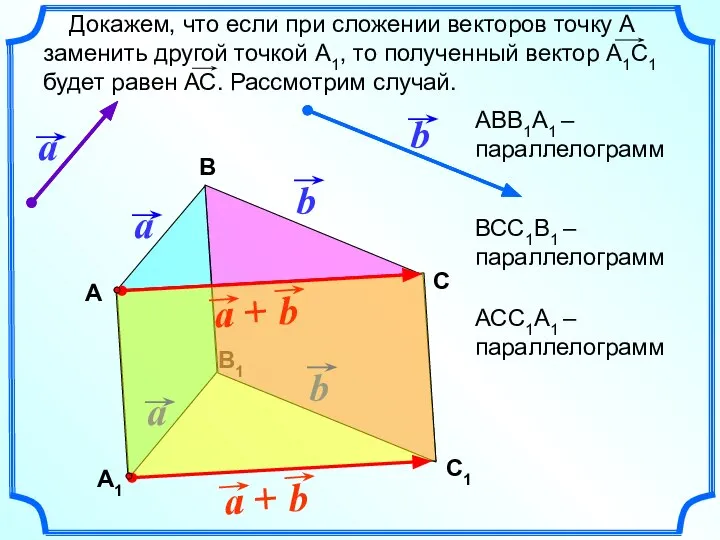
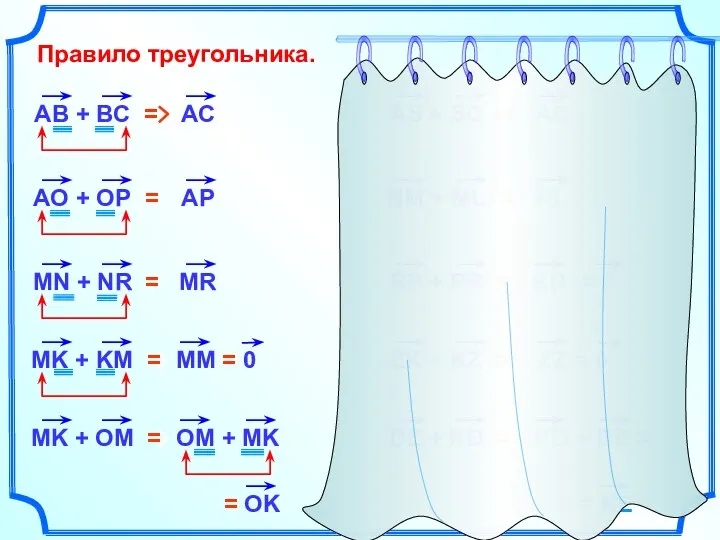
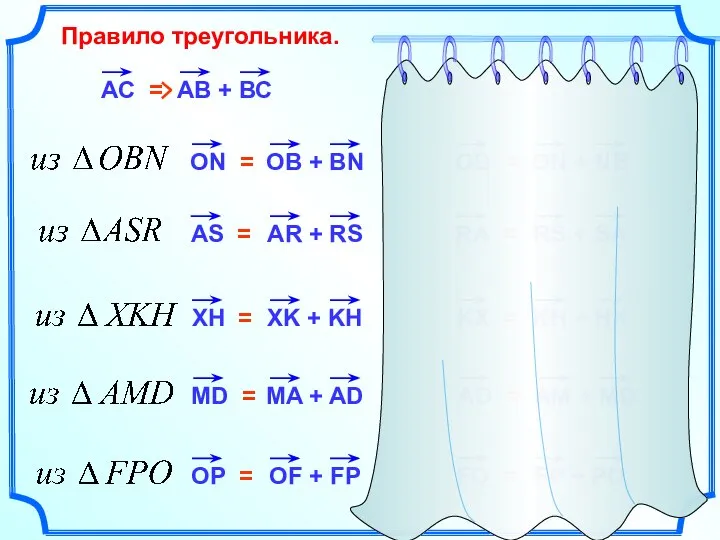
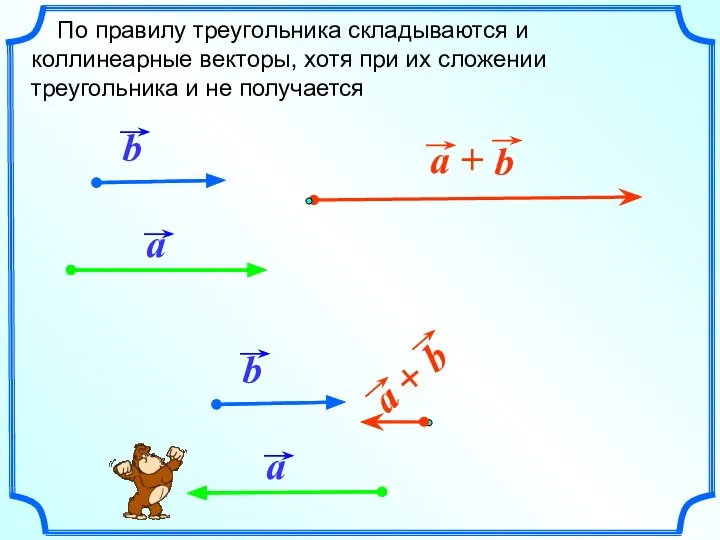
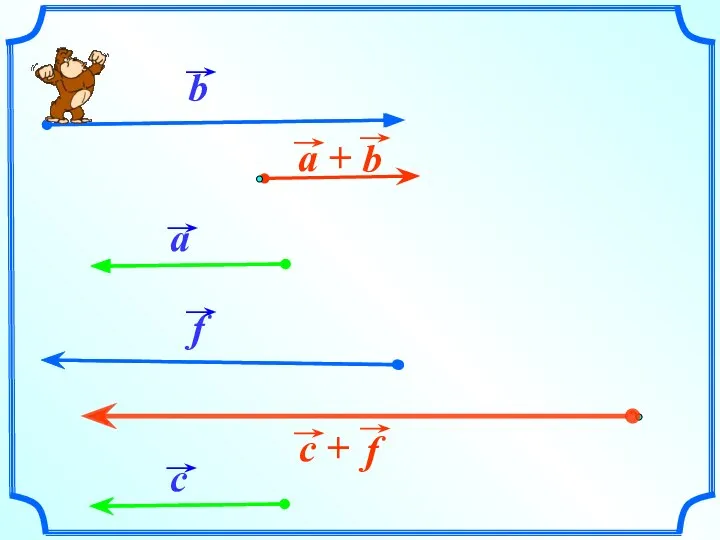

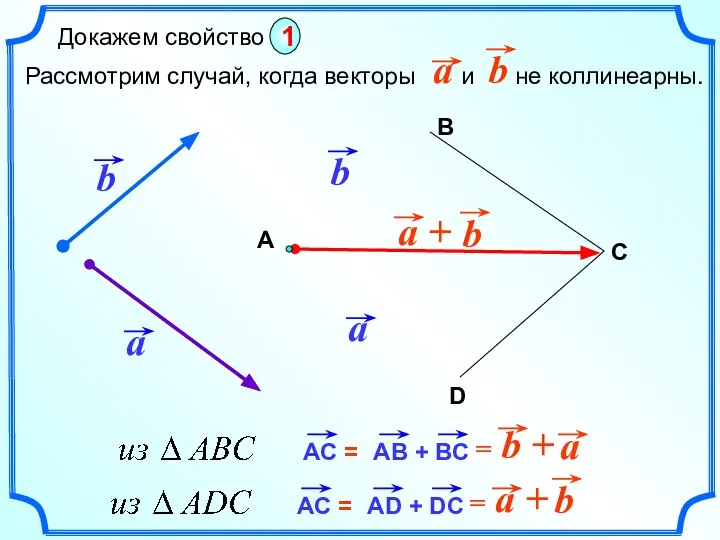
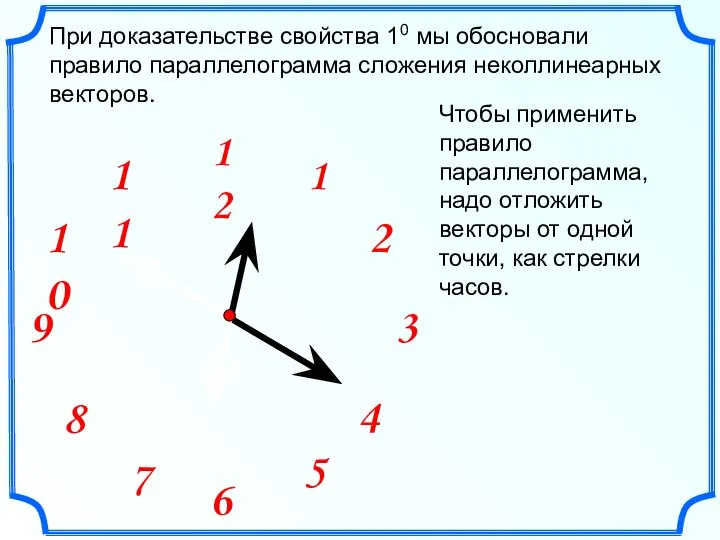

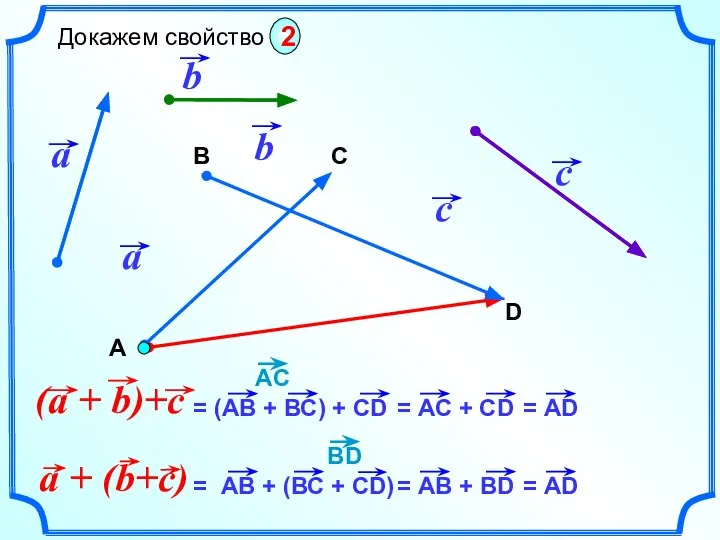
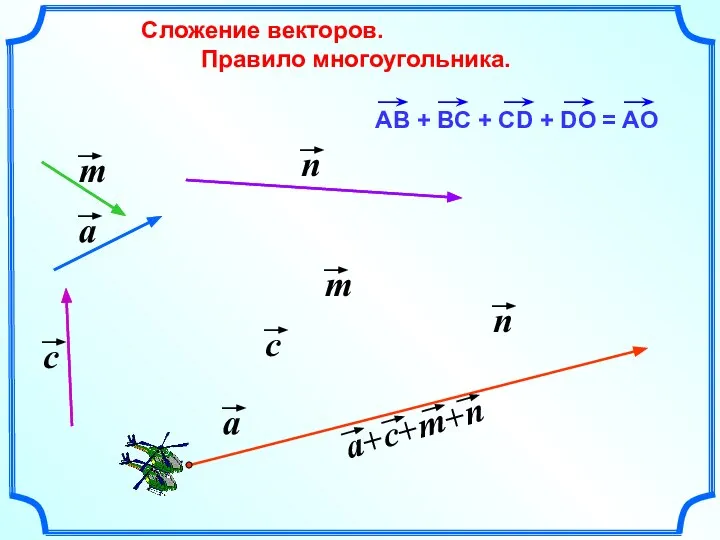
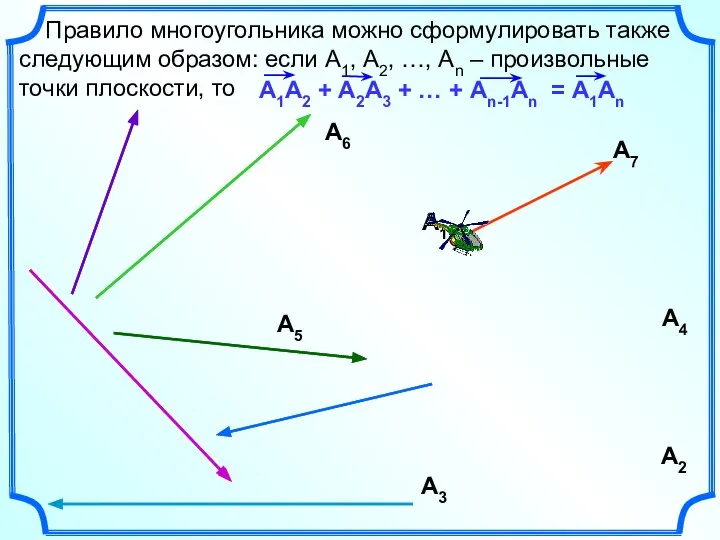
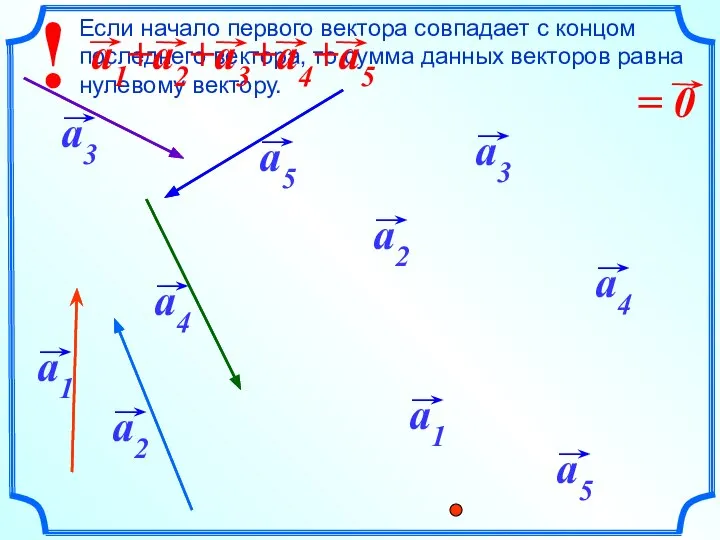
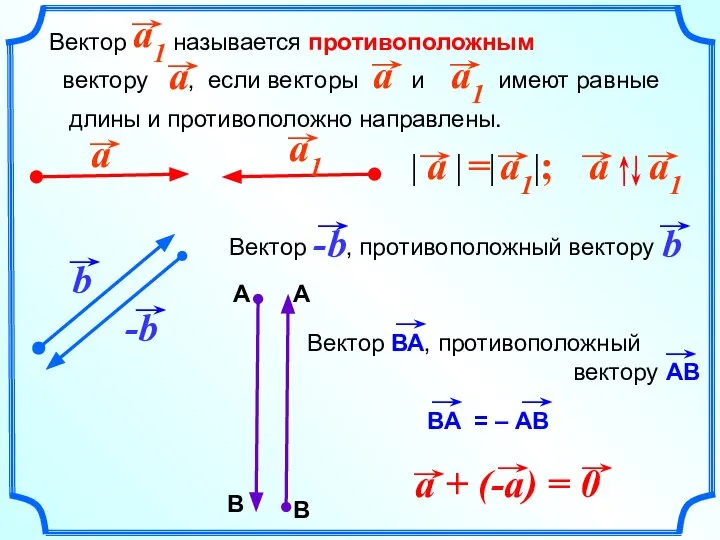
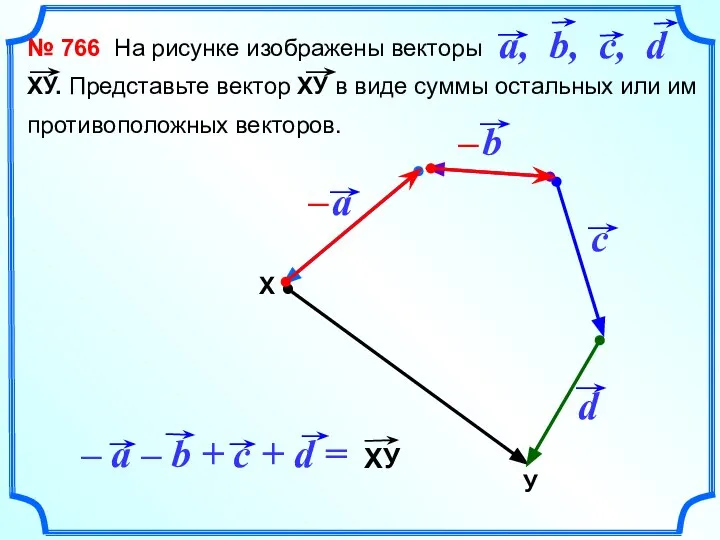
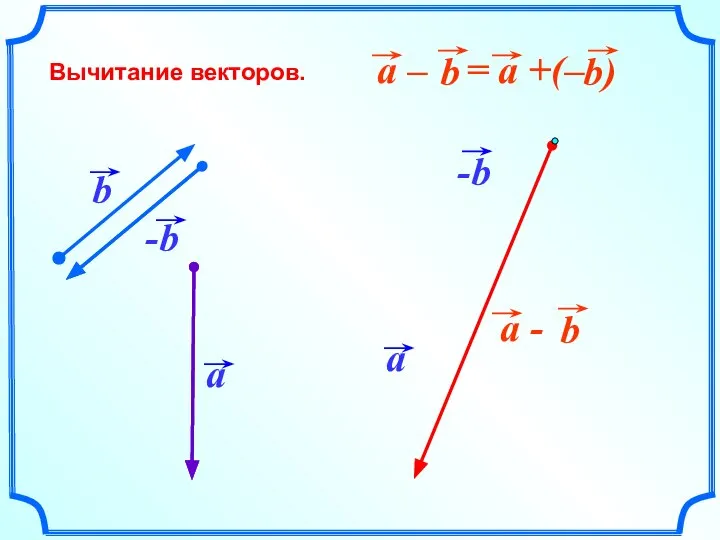
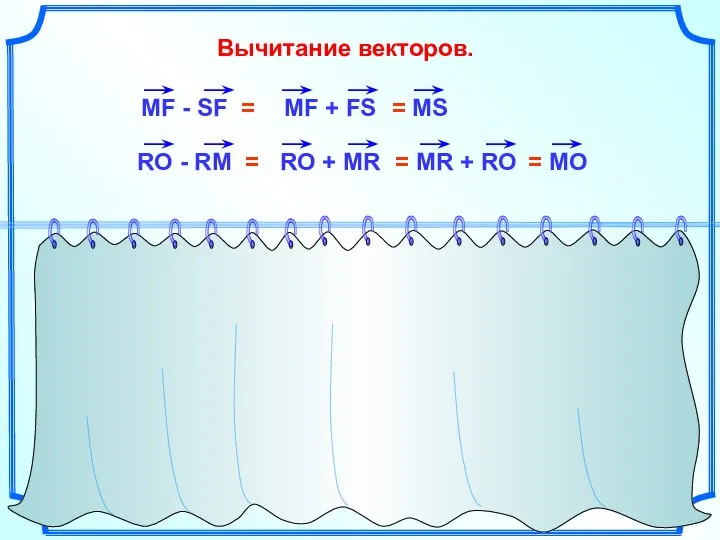
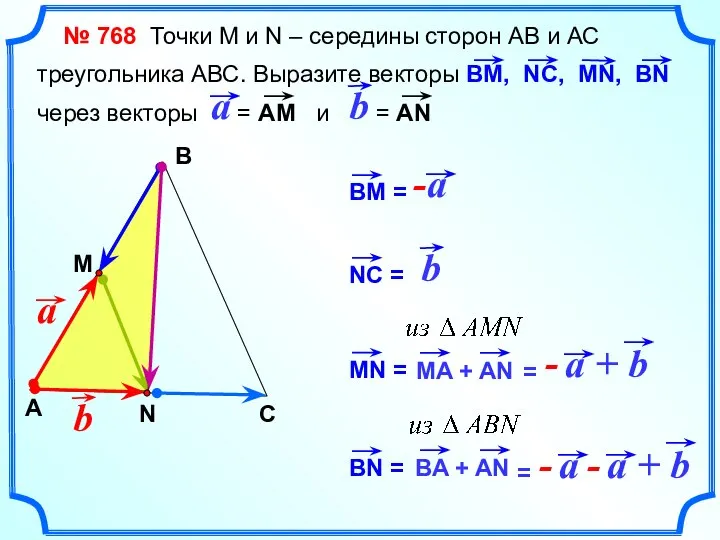
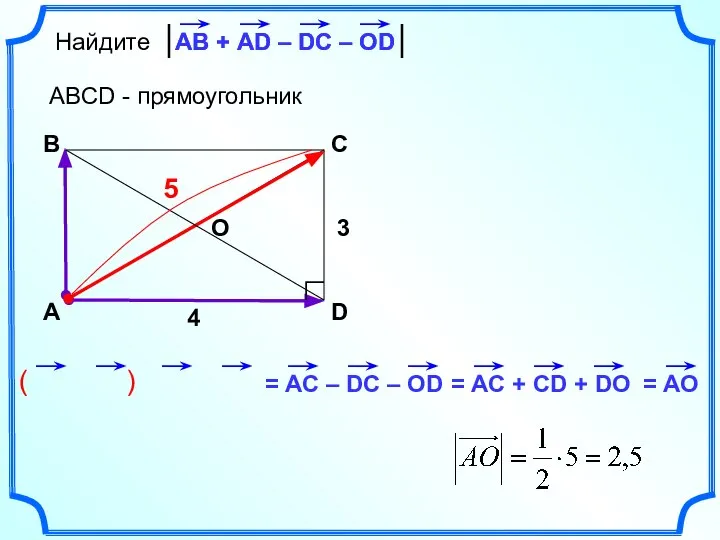
 Таблица единиц площади
Таблица единиц площади Могла ли математика спасти Пахома, или Площадь
Могла ли математика спасти Пахома, или Площадь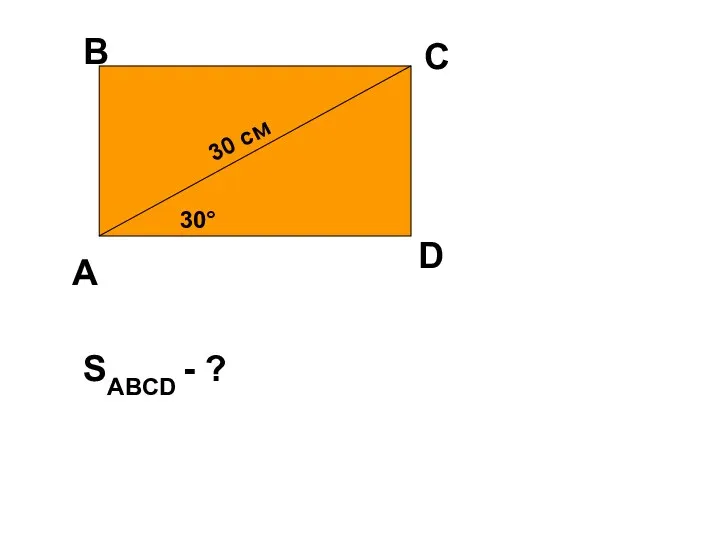 Параметры четырехугольника
Параметры четырехугольника Сложение смешанных чисел
Сложение смешанных чисел Простейшие тригонометрические уравнения. Задания для устного счета
Простейшие тригонометрические уравнения. Задания для устного счета Отношение чисел
Отношение чисел Решение уравнений (часть 2)
Решение уравнений (часть 2) Среднее арифметическое. Среднее значение величины
Среднее арифметическое. Среднее значение величины Углы треугольника
Углы треугольника Тела вращения. Математический диктант
Тела вращения. Математический диктант Координатная плоскость
Координатная плоскость Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим
Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим Частотная таблица
Частотная таблица Решение задач по темам: Параллелограмм, Трапеция, Прямоугольник, Ромб, Квадрат
Решение задач по темам: Параллелограмм, Трапеция, Прямоугольник, Ромб, Квадрат Математические правила и законы
Математические правила и законы Плоскости. Лекция 3
Плоскости. Лекция 3 Цилиндр
Цилиндр Цифра ноль
Цифра ноль Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир
Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир Презентация на тему Пропорциональность величин (6 класс)
Презентация на тему Пропорциональность величин (6 класс)  Степенная функция. Определение
Степенная функция. Определение В путешествие пойдём. В страну чисел попадём
В путешествие пойдём. В страну чисел попадём Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок
Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок Действия со степенями. Срезовая работа для 8 класса
Действия со степенями. Срезовая работа для 8 класса Старинные меры длины на Руси
Старинные меры длины на Руси Сечения многогранников
Сечения многогранников