Развитие понятия о числе

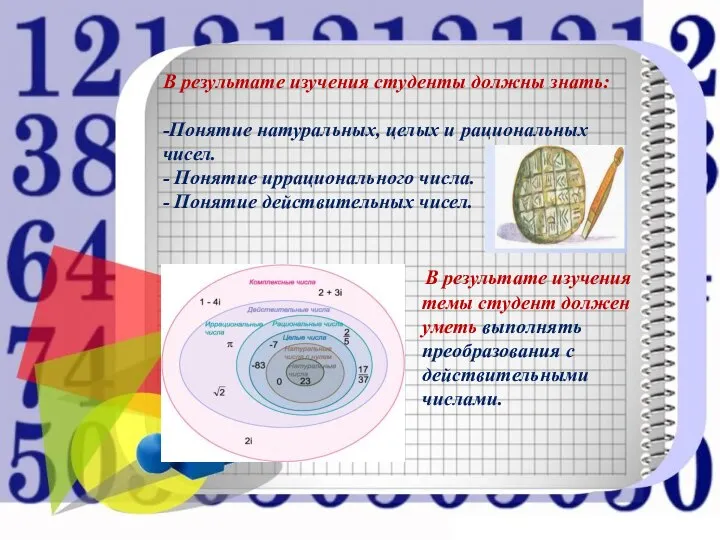
В результате изучения темы студент должен уметь выполнять преобразования с действительными числами.
В результате изучения студенты должны знать:
-Понятие натуральных, целых и рациональных чисел.
- Понятие иррационального числа.
- Понятие действительных чисел.

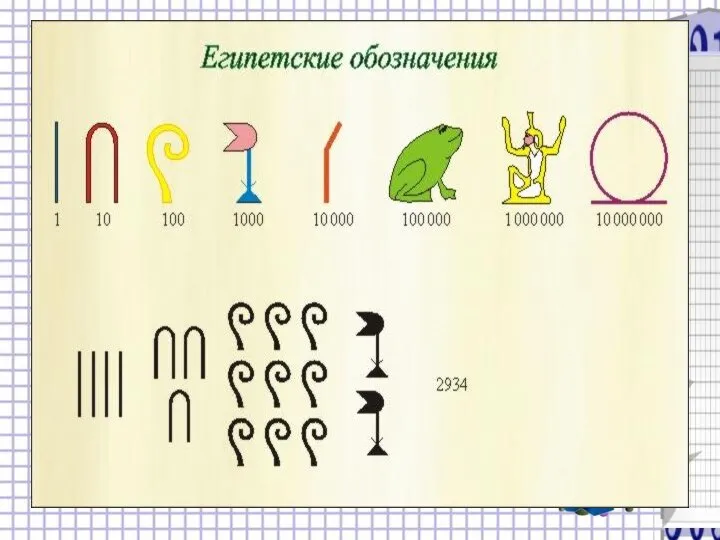
Из истории чисел
Возникнув еще в первобытном обществе из потребностей счета, понятие числа с развитием науки значительно расширилось.
.
На первых этапах существования человеческого общества числа, открытые в процессе человеческой деятельности, служили для примитивного счета предметов, дней, шагов и т.п.
Число- основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций.

Из истории чисел
.
На этом развитие не завершилось. В связи с решением уравнений математики встречались с числом, которое выражалось
С развитием цивилизации ему потребовалось изобретать все большие и большие числа, уметь их записывать. Этот процесс продолжался на протяжении многих столетий и потребовал напряженного интеллектуального труда
Потребовалась не одна сотня лет для того, чтобы математики смогли осмыслить понятие иррационального числа, и выработать способ записи такого числа и приближенного значения его в виде бесконечной десятичной дроби.
.Оно получило название мнимой единицы. После того как норвежский математик Гаспар Вессель (1745-1818) нашел возможность представить мнимое число геометрически, то так называемые «мнимые числа» получили свое место в множестве комплексных чисел.

Из истории чисел
.
На этом развитие не завершилось. В связи с решением уравнений математики встречались с числом, которое выражалось
.
Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали ¼, 1/8, …, затем 1/3, 1/6 и т.д., то есть самые простые дроби, у них числитель всегда единица. Лишь значительно позже у греков, затем у индейцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В дальнейшем оказалось необходимым еще более расширить понятие числа. Последовательно появились числа иррациональные, отрицательные и комплексные.

Из истории чисел
.
На этом развитие не завершилось. В связи с решением уравнений математики встречались с числом, которое выражалось
.
Довольно поздно к семье чисел присоединился нуль. Первоначально слово нуль означало отсутствие числа(буквальный смысл латинского слова nullum –“ничего»). Действительно, если, например, от 3 отнять 3, тоне останется ничего. Для того, чтобы это «ничего» считать числом, появились основания лишь в связи с рассмотрением отрицательных чисел.

Натуральные числа
Натуральные числа (естественные числа) – числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Множество всех натуральных чисел принято обозначать знаком N. Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.

Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
Сложение. Слагаемое + Слагаемое = Сумма
Умножение. Множитель * Множитель = Произведение
Возведение в степень , ab где a — основание степени и b — показатель степени. Если основание и показатель натуральны, то и результат будет являться натуральным числом.
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
Вычитание. Уменьшаемое Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом).
Деление. Делимое / Делитель = (Частное, Остаток).

Целые числа – бывают положительными и отрицательными. Совокупность целых чисел образует множество целых чисел. Число вида а/в,
где а и b целые числа, причём
называется рациональным числом. Множество, состоящее из положительных и отрицательных дробных чисел, называется множеством рациональных чисел.

Основные свойства
Коммутативность сложения. A+B=B+A
Коммутативность умножения. A.B=B.A
Ассоциативность сложения. (A+B)+C=A+(B+C)
Ассоциативность умножения. (AB)C=A(BC)
Дистрибутивность умножения относительно
сложения.

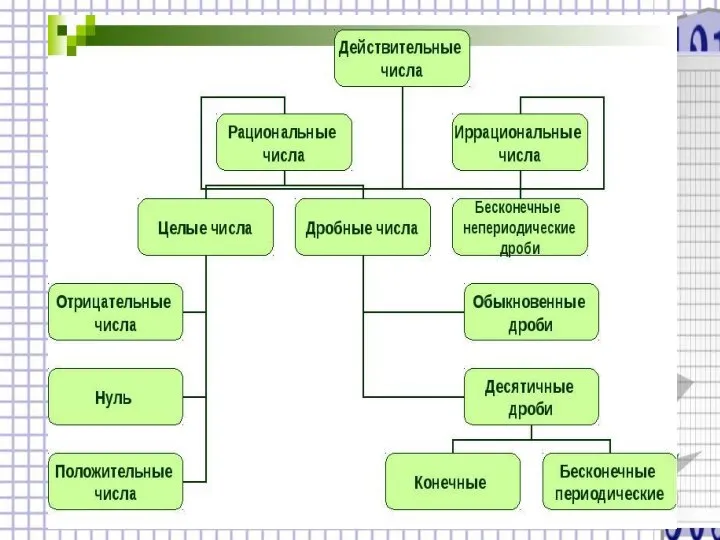
Числовые множества

Любое рациональное число можно представить либо в виде конечной десятичной дроби, либо в виде бесконечной периодической десятичной дроби.

Периодические дроби.
Определение: Периодические дроби бывают чистыми и смешанными.
Чистой периодической называется дробь, у которой период сразу после запятой.
.
Смешанной называется дробь, у которой между запятой и первым периодом есть одна или несколько повторяющихся цифр:
.
142857)

.
Обращение смешанной периодической дроби в обыкновенную:
Чтобы обратить смешанную периодическую дробь достаточно из числа стоящего до второго периода вычесть число стоящее до первого периода, и полученную разность взять числителем , а знаменателем написать цифру в периоде столькими нулями сколько цифр между запятой и периодом:

Комплексные числа
Вид комплексного числа
Х²=-1
Х=i -корень уравнения
i- комплексное число, такое, что i²=-1 Запись комплексного числа в общем виде
А + В i
А и В - действительные числа А - действительная часть
В - мнимая часть
i - мнимая единица
Термин «комплексные числа» ввел немецкий математик Карл Гаус.

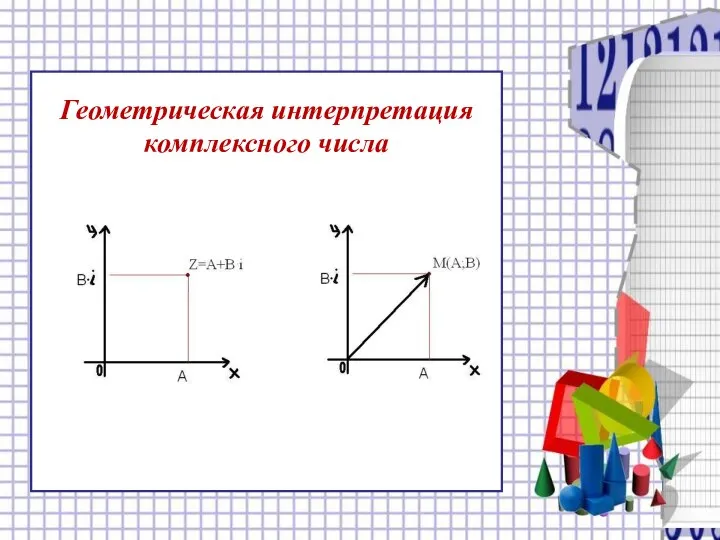
Геометрическая интерпретация комплексного числа

Комплексные взаимносопряженные числа
Z=А - В i
сопряженное
Z= А + В i
Комплексные числа называются взаимно сопряженными, если их действительные части равны, а мнимые отличаются знаками

Комплексные взаимносопряженные числа
Z=А - В i
сопряженное
Z= А + В i