Содержание
- 2. Сочетания Число всех выборов n элементов из m данных без учёта порядка называют числом сочетаний из
- 3. Сочетания Число всех выборов n элементов из m данных без учёта порядка называют числом сочетаний из
- 4. Задача №1 Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать? Решение: Надо
- 5. Задача №2. У Минотавра в лабиринте томятся 25 пленников. а)Сколькими способами он может выбрать себе трёх
- 6. Задача №3 В классе 27 учеников, из них нужно выбрать троих. Сколькими способами это можно сделать,
- 8. Сколькими различными способами из семи участников математического кружка можно составить команду из двух человек для участия
- 9. Задача №5 В отделе работают 5 ведущих и 8 старших сотрудников. В командировку надо послать двух
- 10. Из перетасованной колоды, состоящей из 36 карт, наугад взяты 4 карты. Какова вероятность того, что все
- 11. Задача №7 В партии из 50 деталей находятся 10 бракованных. Вынимают из партии наудачу четыре детали.
- 13. Скачать презентацию










 Логические и традиционные головоломки
Логические и традиционные головоломки Математика. Контрольная работа
Математика. Контрольная работа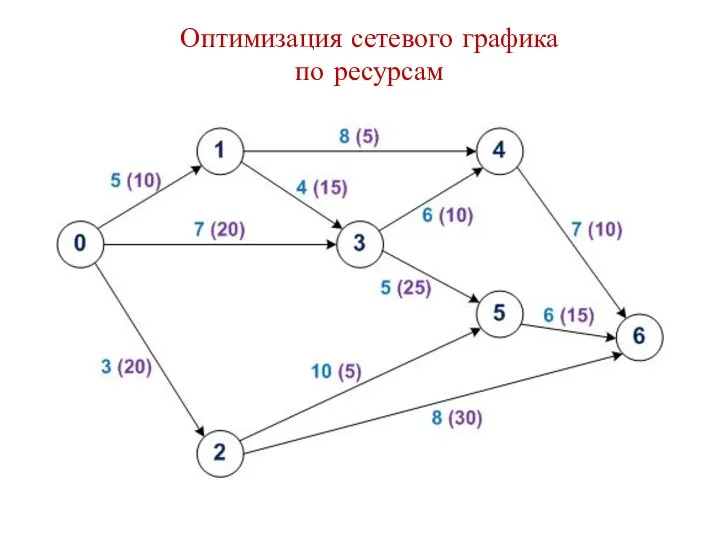 Оптимизация сетевого графика по ресурсам
Оптимизация сетевого графика по ресурсам Признаки равенства треугольников
Признаки равенства треугольников Сравнение двух прогрессий
Сравнение двух прогрессий ОГЭ и ЕГЭ без репетитора. Тренажер
ОГЭ и ЕГЭ без репетитора. Тренажер Решите неравенства
Решите неравенства Биржа знаний
Биржа знаний Равнобедренный треугольник. Интегрированный урок геометрии и русского языка
Равнобедренный треугольник. Интегрированный урок геометрии и русского языка Неравенства и их системы
Неравенства и их системы Разметка прямоугольника по угольнику
Разметка прямоугольника по угольнику Цилиндр. Цилиндры вокруг нас
Цилиндр. Цилиндры вокруг нас Роль математики в медицине
Роль математики в медицине Реализация статистических методов оценки параметров динамической случайной величины
Реализация статистических методов оценки параметров динамической случайной величины Свойства монотонных функций
Свойства монотонных функций Основы метрологии. Международная система единиц физических величин. Закономерности формирования результата измерения
Основы метрологии. Международная система единиц физических величин. Закономерности формирования результата измерения Квадратичная функция. Решение текстовых задач
Квадратичная функция. Решение текстовых задач Многогранники на службе у человека
Многогранники на службе у человека Компланарны ли тройки векторов
Компланарны ли тройки векторов Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость Многогранники. Прямоугольные параллелепипеды
Многогранники. Прямоугольные параллелепипеды Олимпиадная математика (начальная школа)
Олимпиадная математика (начальная школа) Тела вращения. Цилиндр. Площадь поверхности цилиндра
Тела вращения. Цилиндр. Площадь поверхности цилиндра Степень с рациональным показателем. Самостоятельная работа
Степень с рациональным показателем. Самостоятельная работа Площадь квадрата, прямоугольника, параллелограмма
Площадь квадрата, прямоугольника, параллелограмма Численные методы решения СЛАУ (часть 1)
Численные методы решения СЛАУ (часть 1)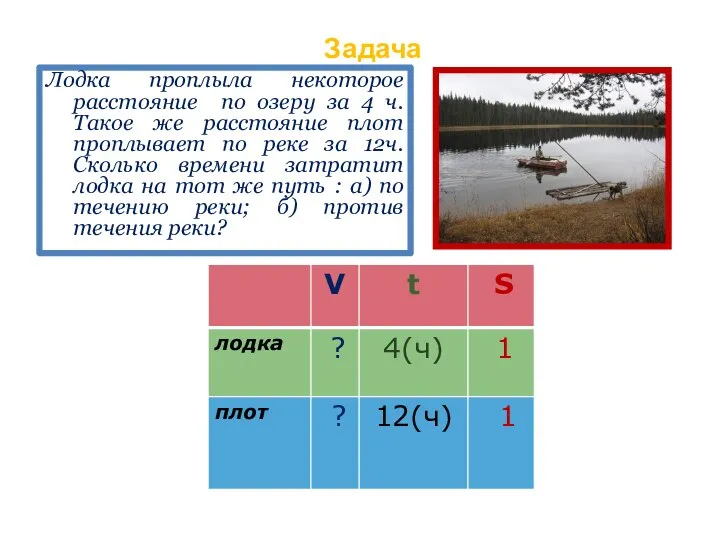 Движение как работа
Движение как работа История математики. Брейн-ринг, 10 класс
История математики. Брейн-ринг, 10 класс