Наибольшее и наименьшее значение функций

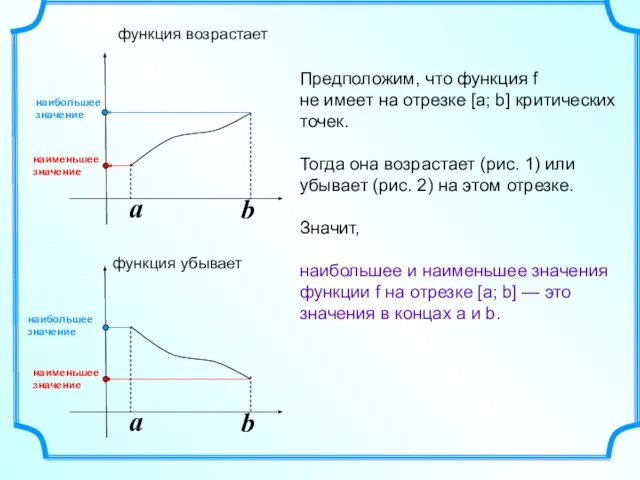
a
b
a
b
Предположим, что функция f
не имеет на отрезке [а; b] критических точек.
Тогда она возрастает (рис. 1) или убывает (рис. 2) на этом отрезке.
Значит,
наибольшее и наименьшее значения функции f на отрезке [а; b] — это значения в концах а и b.
функция возрастает
функция убывает

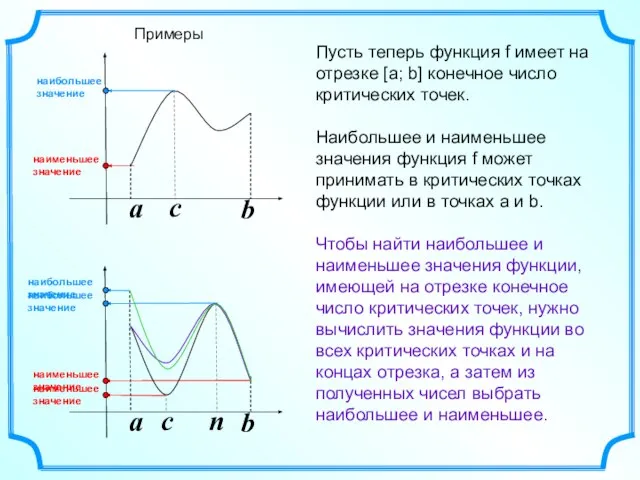
a
b
a
b
Пусть теперь функция f имеет на отрезке [а; b] конечное число критических точек.
Наибольшее и наименьшее значения функция f может принимать в критических точках функции или в точках а и b.
Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Примеры

Вывод :
Если поведение функции постоянно внутри отрезка, то своего наибольшего и наименьшего значения она достигает в концах отрезка
Если поведение функции внутри отрезка не постоянно, то функция может достигать своего наибольшего и наименьшего значения либо в концах отрезка, либо в точках экстремума

Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
1.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
1) y(0) = 0
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в критических точках, которые принадлежат заданному отрезку.

Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3) y(0) = 0
Выполнение этапов решения можно изменить, как вам удобно.

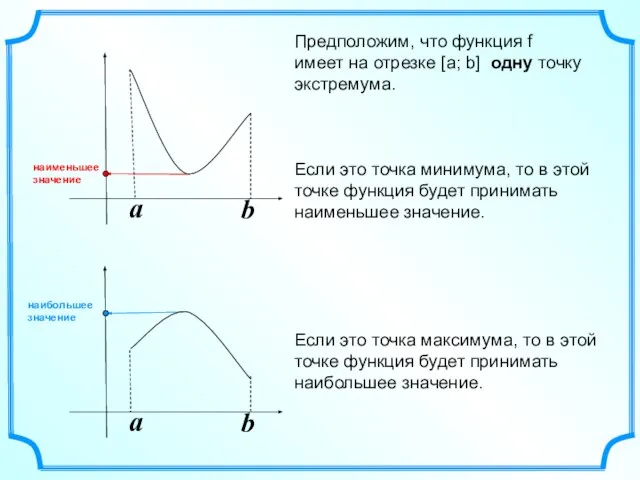
a
b
a
b
Предположим, что функция f
имеет на отрезке [а; b] одну точку экстремума.
Если это точка минимума, то в этой точке функция будет принимать наименьшее значение.
Если это точка максимума, то в этой точке функция будет принимать наибольшее значение.

Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3)
Другой способ решения
min
Наименьшее значение функция будет принимать в точке минимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в концах отрезка будет сложным.

Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из полученных значений.
1) y(0) = 4
2) y / = 3x2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
2.

Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
1) y(1) = 1 – 2 + 1 + 3 = 3
y(4) = 43– 2 42 + 4 + 3 = 39
2) y / = 3x2 – 4x + 1=
y(1) = 3
Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наименьшее значение функции y = x3 – 2x2 + x +3
на отрезке [ 1; 4 ]
3.
3x2 – 4x + 1 = 0
D=16–4*3*1=4

Найдите наибольшее значение функции
на отрезке [ -3; 3 ]
4.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из
полученных значений.
y(-3) = 11
Значения функции в критических точках, которые принадлежат заданному отрезку.
y(-3) = -25

Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
5.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.

Найдите наименьшее значение функции
на отрезке [ 1; 9 ]
6.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.

Найдите наименьшее значение функции
на отрезке [-10; 1 ]
7.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.

Найдите наименьшее значение функции
на отрезке [-10; 1 ]
7.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.

Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
8.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Запишем функцию в удобном для дифференцирования виде

Найдите наибольшее значение функции
на отрезке [ 3; 10 ]
9.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
1). Первое число меньше 1, т.к. знаменатель e4 > 5.
2). Второе число – отрицательноe.
3). Значит, наибольшее число 1.
1

Найдите наименьшее значение функции
на отрезке [ 1; 7 ]
10.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Наименьшее число – 4, т.к. первые два положительные.
1

Найдите наибольшее значение функции
y = ln(x+5)5 – 5x на отрезке [-4,5; 0]
11.
max
Наибольшее значение функция будет принимать в точке максимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
y = 5ln(x+5) – 5x
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
3. Вычислить значения функции в критических точках
и на концах отрезка.
4. Из вычисленных значений выбрать наименьшее или наибольшее.
0
Можно рассуждать иначе
Запишем функцию в удобном для дифференцирования виде

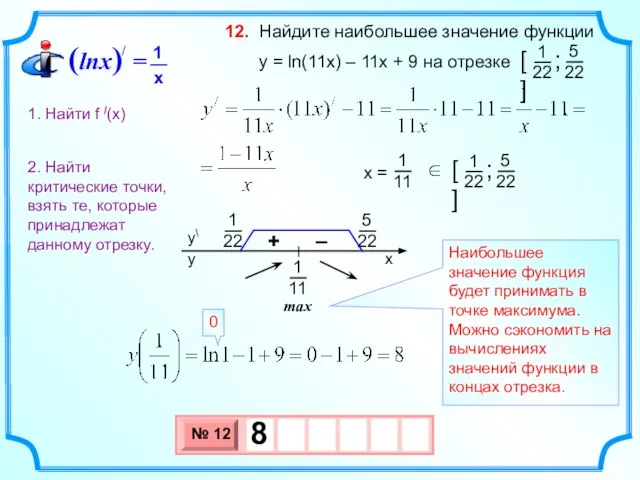
Найдите наибольшее значение функции
y = ln(11x) – 11x + 9 на отрезке
12.
max
Наибольшее значение функция будет принимать в точке максимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0

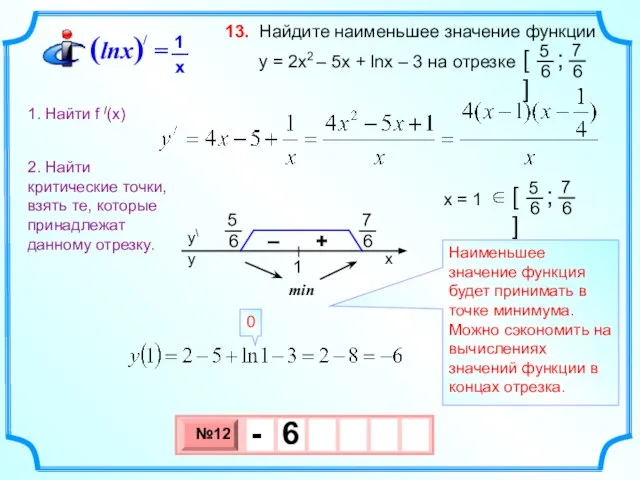
Найдите наименьшее значение функции
y = 2х2 – 5x + lnx – 3 на отрезке
13.
min
Наименьшее значение функция будет принимать в точке минимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0

Найдите наибольшее значение функции
y = 7cosx +16x – 2 на отрезке
14.
Функция на всей области определения возрастает. Нетрудно догадаться, что у / > 0.
Тогда наибольшее значение функция будет иметь в правом конце отрезка, т.е. в точке х=0.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Если вы не догадались, то вычислите значения функции в каждом конце отрезка и выберите наибольшее.
0

Критических точек нет.
Тогда наибольшее значение функция будет принимать в одном из концов отрезка.
Можно было и раньше догадаться, что наибольшее значение будет именно в левом конце отрезка! Как?
Найдите наибольшее значение функции
y = 10sinx – x + 7 на отрезке
15.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0

Функция на всей области определения убывает. Нетрудно догадаться, что у / < 0.
Тогда наименьшее значение функция будет иметь в правом конце отрезка, т.е. в точке х=0.
Найдите наименьшее значение функции
y = 5cosx – 6x + 4 на отрезке
16.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
1
0
Если вы не догадались, то вычислите значения функции в каждом конце отрезка и выберите наименьшее.

Найдите наибольшее значение функции
y = 12cosx + 6 x – 2 + 6 на отрезке
17.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.

Найдите наибольшее значение функции
y = 12cosx + 6 x – 2 + 6 на отрезке
17.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Убедимся, что данная точка является точкой максимума на заданном промежутке.
Значит, наибольшее значение функция достигает именно в этой точке.
Тогда значения функции в концах отрезка можно не считать.
Можно рассуждать иначе
max

Найдите наименьшее значение функции
y = 11 + – х – cosx на отрезке
18.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Можно убедиться, что данная точка является точкой минимума на заданном промежутке.
Значит, наименьшее значение функция достигает именно в этой точке.
Тогда значения функции в концах отрезка можно не считать.
min

Найдите наименьшее значение функции
y = 4tgx – 4x – + 5 на отрезке
19.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0

Найдите наибольшее значение функции
y = 3tgx – 3x + 5 на отрезке
20.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
-1
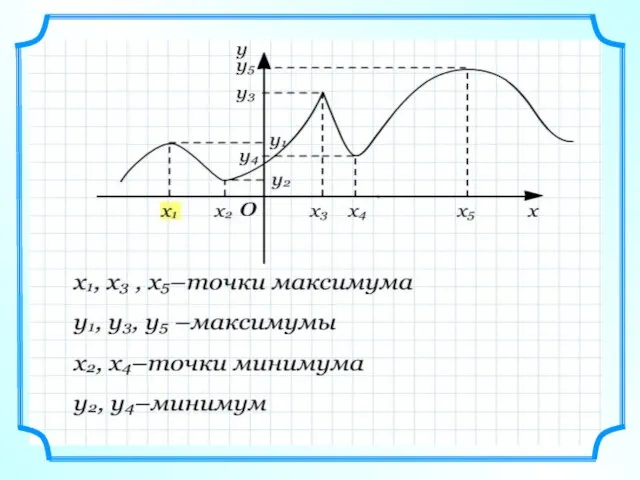
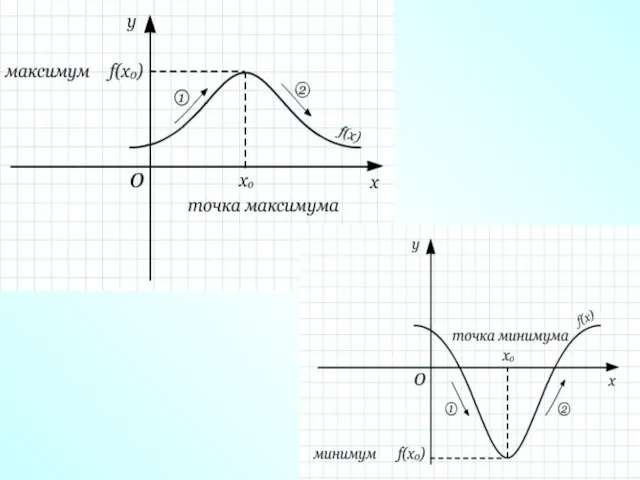
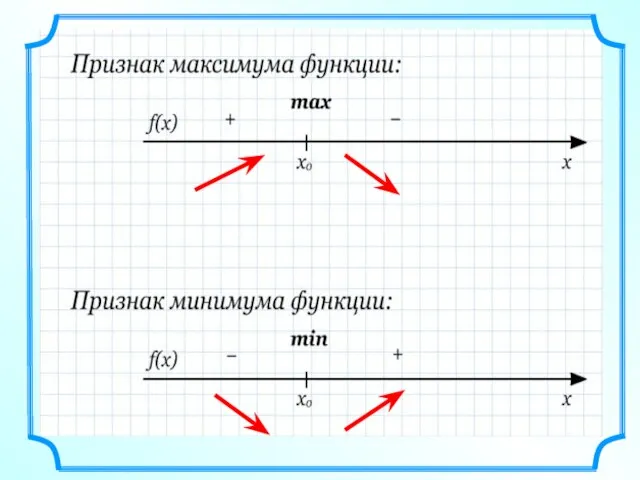
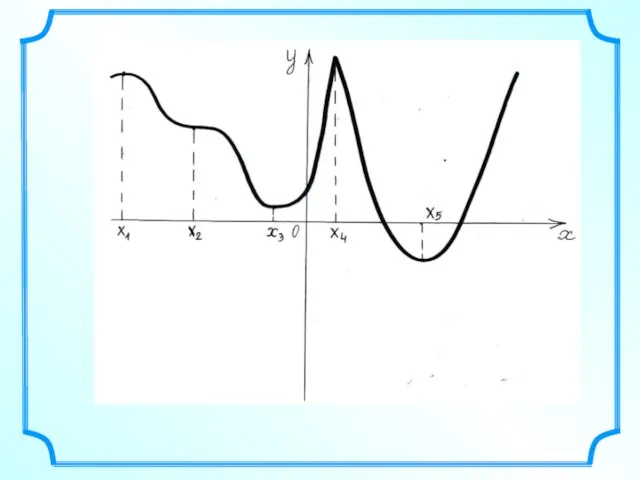
0

Нахождение точек
минимума (min)
и максимума (max)
функции

Найти производную функции.
Решить уравнение f ´(х)=0, и найти тем самым стационарные точки.
Методом интервалов установить промежутки знакопостоянства производной.
Если при переходе через точку х0:
- производная не меняет знак, то х0 – точка перегиба;
- производная меняет знак с «+» на «-», то х0 точка максимума;
- производная меняет знак с «-» на «+», то х0 точка минимума.
Алгоритм нахождения точек экстремума: