Содержание
- 2. Устная работа - разминка
- 3. 1. Разложите на множители: а) б) в) г) д) е)
- 4. Найдите ошибки:
- 5. Разложите на множители:
- 6. Теория:
- 7. Исследовательская работа 1 2 3
- 8. Исследовательская работа 6 5 4
- 11. Выполним действия с многочленами. (6a+6b):(a +b)= разложим многочлен в числителе на множители: 6.
- 12. Продолжим. Выполним деление: (a-b):(a²-b²)= Разложим многочлен в знаменателе на множители: 1 Получили алгебраическую дробь.
- 13. Алгоритм сокращения алгебраических дробей: Разложить, по возможности, числитель и знаменатель на множители. Разделить одновременно числитель и
- 14. Сократите дроби (письменно):
- 15. 2. Сократите дроби (письменно) а) б) в) г)
- 16. 4. При каких значениях р возможно сокращение дроби
- 17. Самостоятельная работа
- 18. 3. Найдите значение алгебраической дроби, предварительно сократив ее: при х=10, х=0, х=5, х=2. Всегда ли это
- 19. Запомним !
- 20. Буквы могут принимать лишь допустимые значения, т. е. такие значения, при которых знаменатель этой дроби не
- 21. Найти допустимые значения букв, входящих в дробь: любое действительное число
- 22. Работа на уроке № 430 (нечетные)
- 23. Найдите допустимые значения алгебраической дроби
- 24. Основное свойство дроби
- 26. Скачать презентацию























 32046
32046 Признак параллельности прямых. Задачи для устной работы
Признак параллельности прямых. Задачи для устной работы Показатели вариации
Показатели вариации Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Геометрические тела. Многогранники
Геометрические тела. Многогранники Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Понятие производной
Понятие производной Tema1_TeoriaMnozhestv
Tema1_TeoriaMnozhestv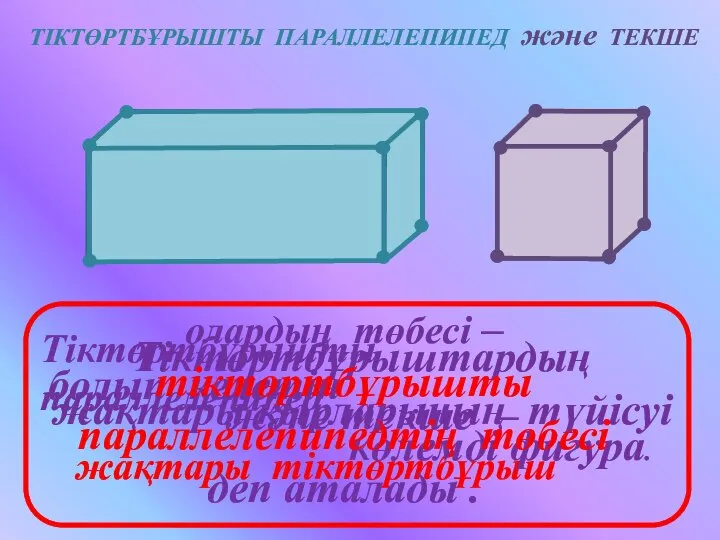 Тіктөртбұрышты параллелепипед және текше
Тіктөртбұрышты параллелепипед және текше Свойства логарифмов
Свойства логарифмов Элементы геометрии на небесной сфере. Лекция 1
Элементы геометрии на небесной сфере. Лекция 1 Признаки параллелограмма
Признаки параллелограмма Найдите все значения параметра a,
Найдите все значения параметра a, аксиомы стереометрии
аксиомы стереометрии Практикум по решению задач практической направленности
Практикум по решению задач практической направленности Умножение дробей
Умножение дробей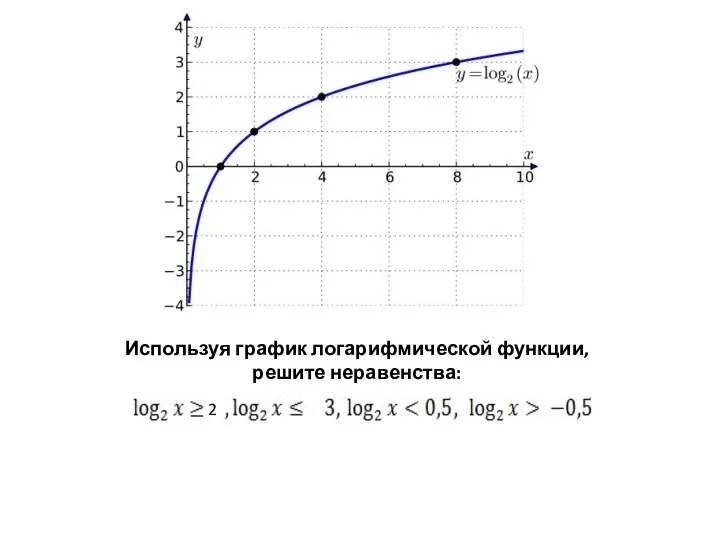 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма
Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма угол между прямой и плоскостью (1)
угол между прямой и плоскостью (1) Учимся писать цифры
Учимся писать цифры Векторы. Нулевой вектор
Векторы. Нулевой вектор Сравнение дробей. 1 часть
Сравнение дробей. 1 часть Живая планета!
Живая планета! Преобразование иррациональных выражений
Преобразование иррациональных выражений Арифметичская прогрессия
Арифметичская прогрессия Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Волшебная страна математики: основы математики для детей 5-6 лет
Волшебная страна математики: основы математики для детей 5-6 лет Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника