Содержание
- 2. Содержание: 1.) Определение призмы. 2.) виды призм: - прямая призма; - наклонная призма; - правильная призма;
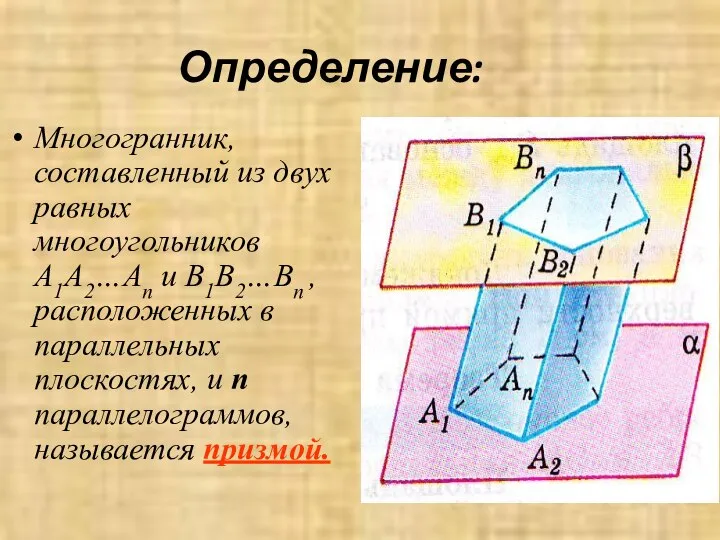
- 3. Определение: Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn , расположенных в параллельных плоскостях, и
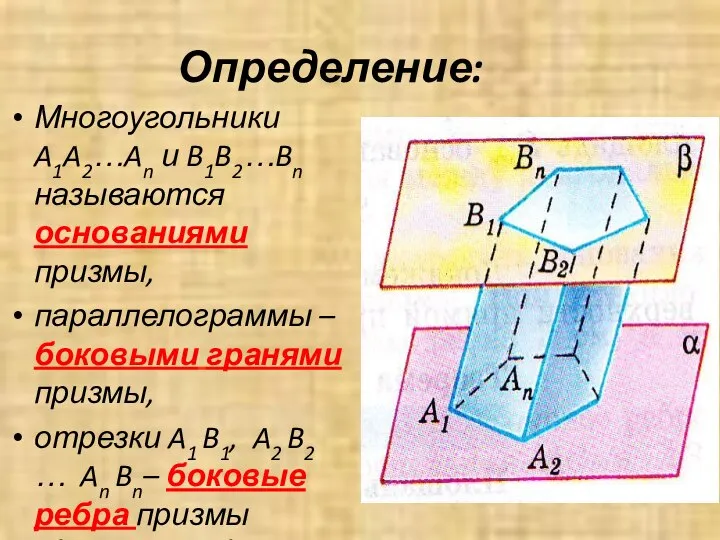
- 4. Определение: Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы, параллелограммы – боковыми гранями призмы, отрезки A1 B1,
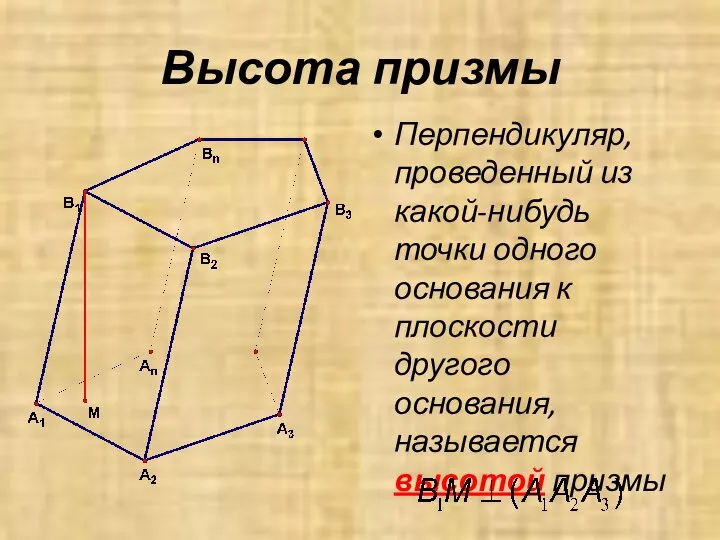
- 5. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы Высота призмы
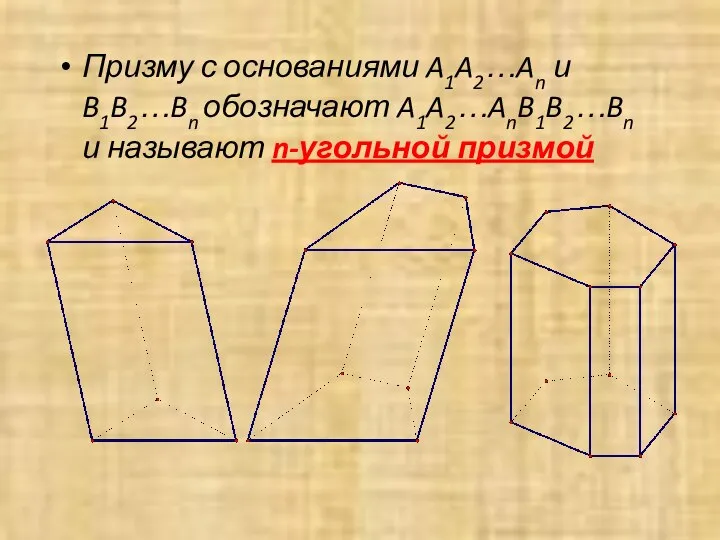
- 6. Призму с основаниями A1A2…An и B1B2…Bn обозначают A1A2…AnB1B2…Bn и называют n-угольной призмой
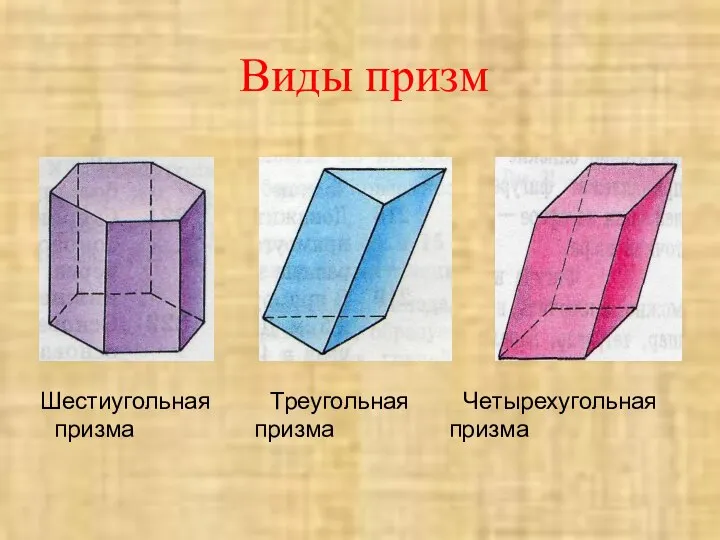
- 7. Виды призм Шестиугольная Треугольная Четырехугольная призма призма призма
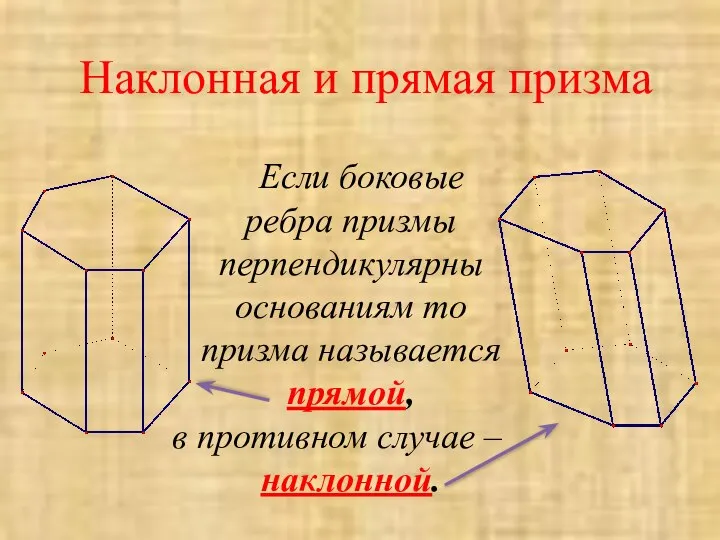
- 8. Наклонная и прямая призма Если боковые ребра призмы перпендикулярны основаниям то призма называется прямой, в противном
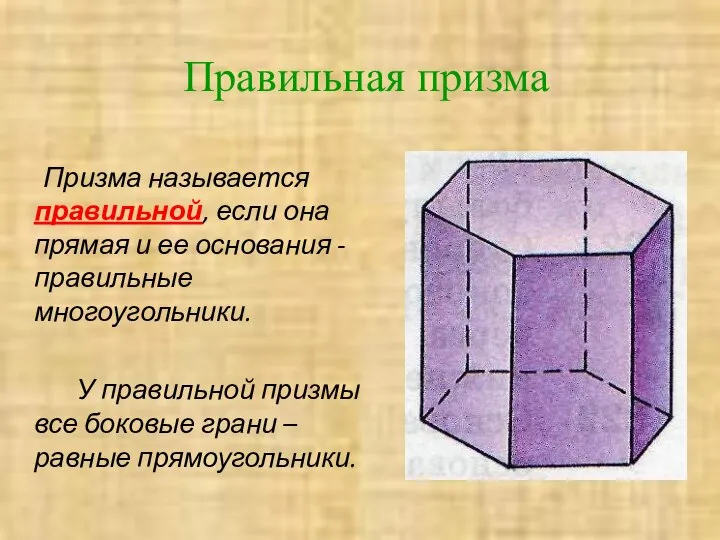
- 9. Правильная призма Призма называется правильной, если она прямая и ее основания - правильные многоугольники. У правильной
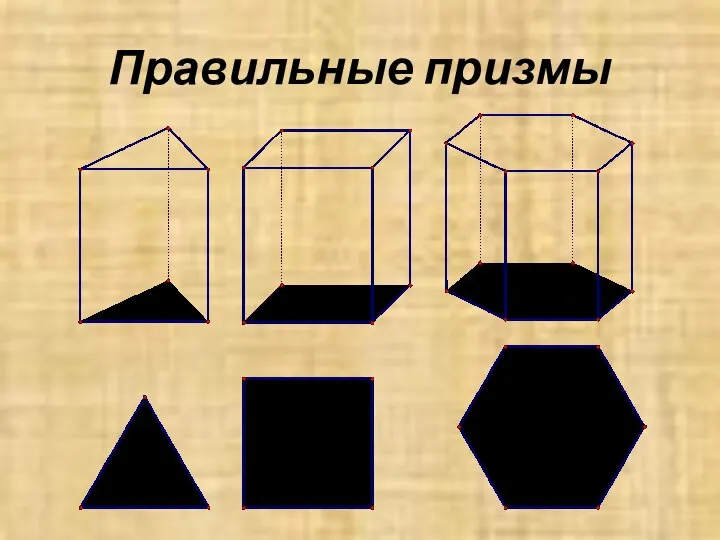
- 10. Правильные призмы
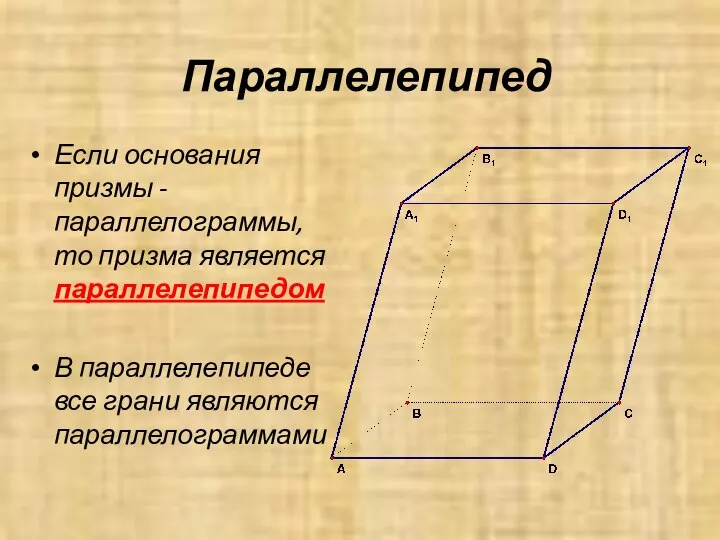
- 11. Параллелепипед Если основания призмы - параллелограммы, то призма является параллелепипедом В параллелепипеде все грани являются параллелограммами
- 12. Площадь полной поверхности призмы Площадью полной поверхности призмы называется сумма площадей ее боковых граней и площадей
- 13. Теорема о площади боковой поверхности прямой призмы Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра
- 14. Призмы встречающиеся в жизни
- 15. Применение призмы в архитектуре
- 16. Применение призмы в быту.
- 17. Задача на нахождение Sполн призмы. Вычислить площадь полной поверхности, если высота равна 12см, а сторона основания
- 18. Решение: Ответ: полн полн
- 20. Скачать презентацию








 Системы счисления
Системы счисления Первообразная. Таблица для нахождения первообразных элементарных функций
Первообразная. Таблица для нахождения первообразных элементарных функций Специальная теория относительности
Специальная теория относительности Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Свойства степени
Свойства степени Тесты по математике
Тесты по математике Сложение вида +6
Сложение вида +6 Задание 19. Профиль (1)
Задание 19. Профиль (1)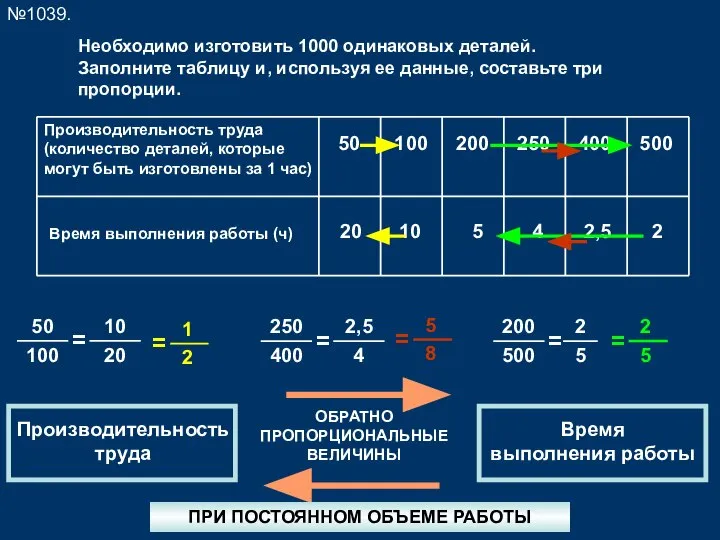 Пропорциональные величины
Пропорциональные величины Скалярное произведение векторов
Скалярное произведение векторов Случаи вычитания 12 -
Случаи вычитания 12 - Устный счёт. Транспорт
Устный счёт. Транспорт Как посчитать консонанс
Как посчитать консонанс Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников 1155274
1155274 Векторная алгебра
Векторная алгебра ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах
ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах Логика предикатов
Логика предикатов Возвратные уравнения
Возвратные уравнения Параллельность прямых
Параллельность прямых Формула Пика
Формула Пика Первообразная. Таблица первообразных
Первообразная. Таблица первообразных урок 1,2 по геометрии 11 класс 6 сентября 2022
урок 1,2 по геометрии 11 класс 6 сентября 2022 Решение экономических задач
Решение экономических задач Использование циклов
Использование циклов Устный счёт
Устный счёт Формулы для решения С2 координатно-векторным способом
Формулы для решения С2 координатно-векторным способом