Содержание
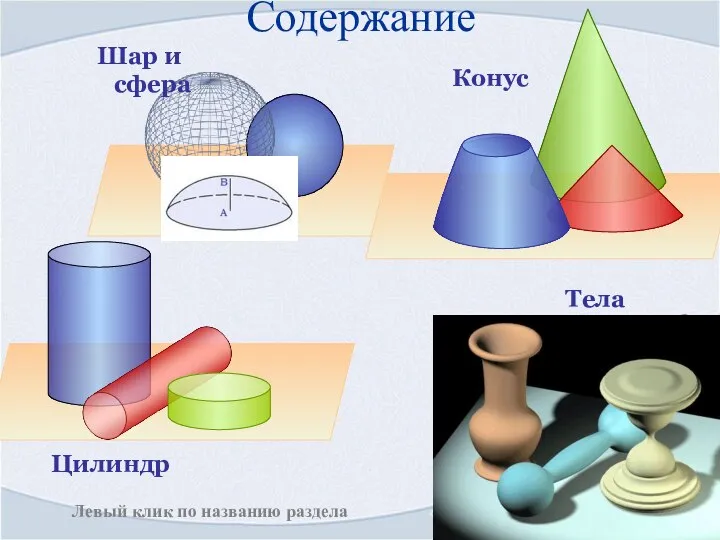
- 2. Цилиндр Конус Шар и сфера Тела вращения Содержание Левый клик по названию раздела
- 3. Тело вращение – это пространственная фигура полученная вращением плоской ограниченной области вместе со своей границей вокруг
- 4. Задание 1) Приведите примеры из окружающего мира тел, похожих на тело полученное вращением треугольника вокруг оси,
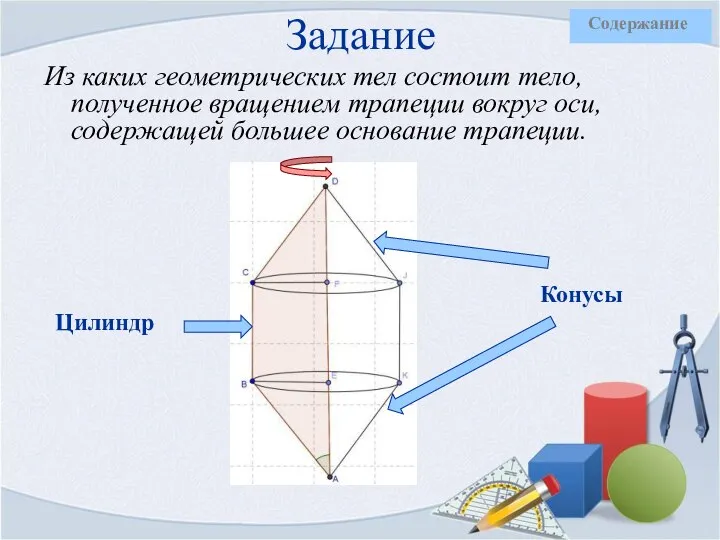
- 5. Задание Из каких геометрических тел состоит тело, полученное вращением трапеции вокруг оси, содержащей большее основание трапеции.
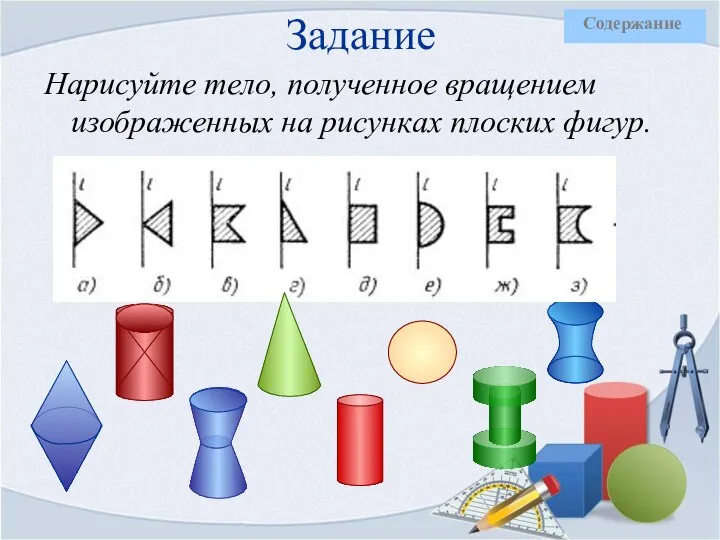
- 6. Задание Нарисуйте тело, полученное вращением изображенных на рисунках плоских фигур. Проверка
- 7. Задание Нарисуйте тело, полученное вращением изображенных на рисунках плоских фигур.
- 8. Задание Нарисуйте плоскую фигуру, вращая которую можно получить изображенное тело. А) Б) В) Г) Д)
- 9. Цилиндр Зададим две параллельные плоскости α и β. В плоскости α расположим окружность некоторого радиуса. Если
- 10. Цилиндр Цилиндр – это тело, которое описывает прямоугольник при вращении около оси, содержащей его сторону. Верхний
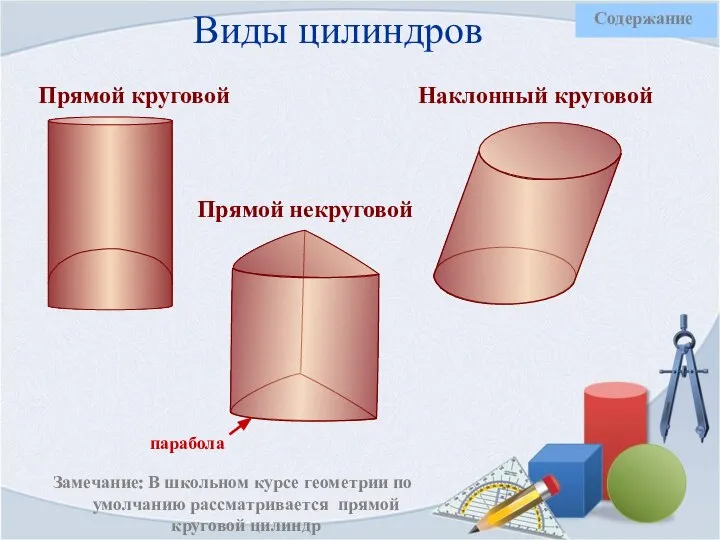
- 11. Виды цилиндров Прямой круговой Прямой некруговой Наклонный круговой Замечание: В школьном курсе геометрии по умолчанию рассматривается
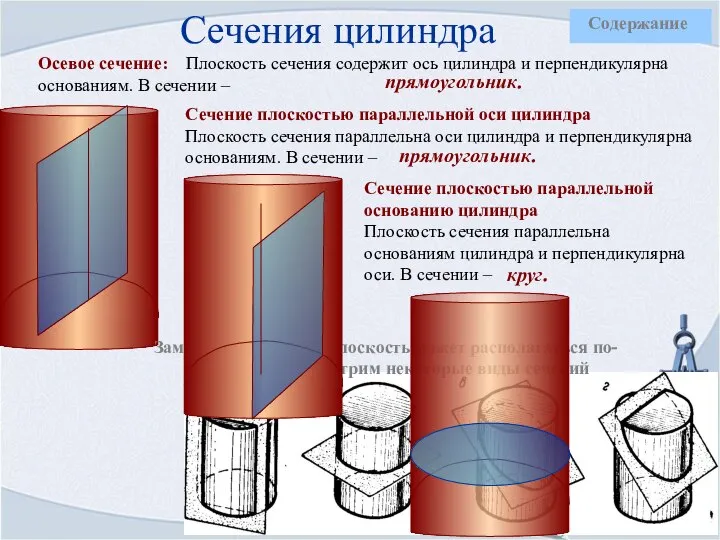
- 12. Сечения цилиндра Осевое сечение: Плоскость сечения содержит ось цилиндра и перпендикулярна основаниям. В сечении – Замечание:
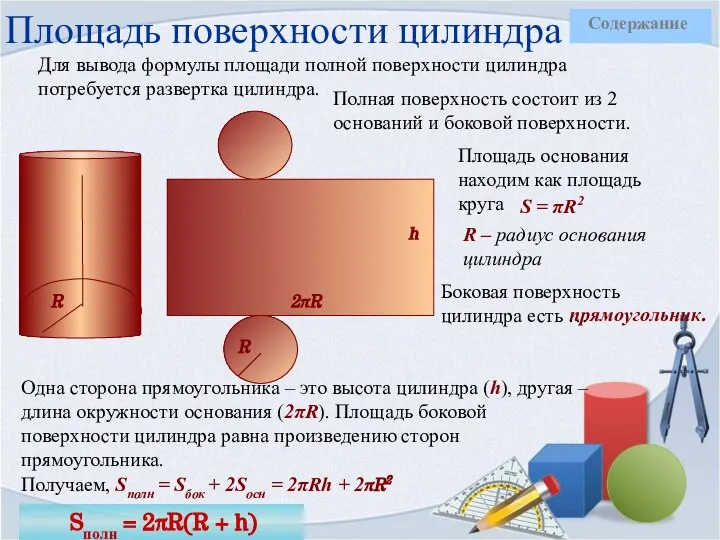
- 13. Площадь поверхности цилиндра Для вывода формулы площади полной поверхности цилиндра потребуется развертка цилиндра. Sполн = 2πR(R
- 14. Решение устных задач с цилиндром 1)Во сколько раз увеличится боковая поверхность цилиндра, если его высота увеличится
- 15. Решение устных задач с цилиндром 3) Осевые сечения двух цилиндров равны. Равны ли высоты этих цилиндров?
- 16. Решение задач с практическим содержанием 5) Найдите площадь листа жести, если из него изготовлена труба длиной
- 17. Решение задачи 5 d = 32 cм = 0,32 м; d = 2R Sбок= πdh; Sбок
- 18. Решение задачи 6 Sматериала = n· Sбанки 1) Найдем количество материала на изготовление 1 банки: d
- 19. Решение задачи 8 1) Вычислим площадь поверхности, которую нужно покрасить: Sсвода = 0,5Sбок=0,5 ·2·2,9 ·6π =
- 20. Решение задачи 7 1) Вычислим площадь поверхности котла, который имеет цилиндрическую форму: Sполн = 2πR(R+h)=2 ·
- 21. Конус Зададим плоскость α и точку С вне этой плоскости. В плоскости α расположим окружность некоторого
- 22. Конус – это тело, которое описывает прямоугольный треугольник при вращении вокруг оси, содержащей его катет. Круг
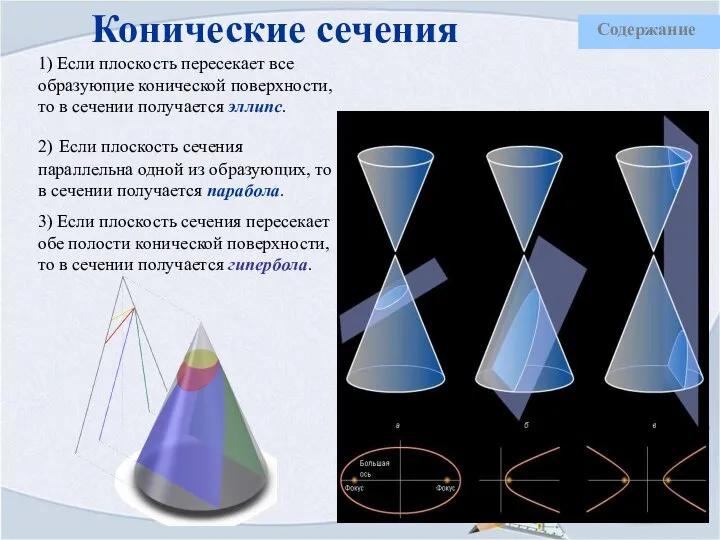
- 23. Конические сечения 1) Если плоскость пересекает все образующие конической поверхности, то в сечении получается эллипс. 2)
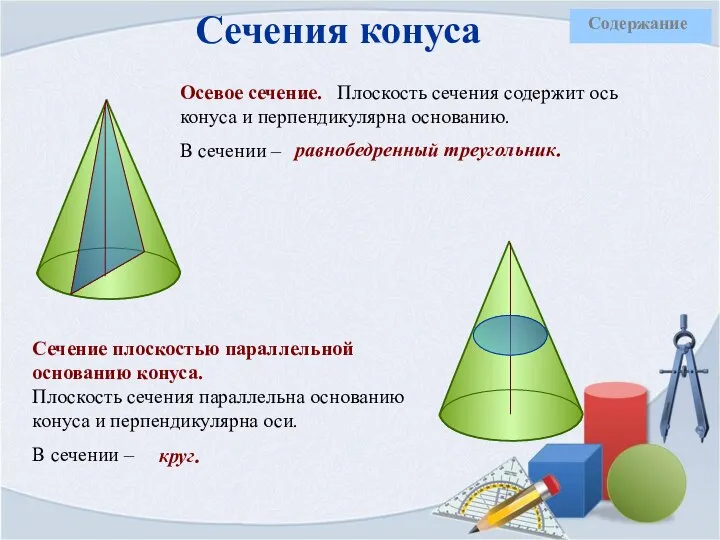
- 24. Сечения конуса Осевое сечение. Плоскость сечения содержит ось конуса и перпендикулярна основанию. В сечении – Сечение
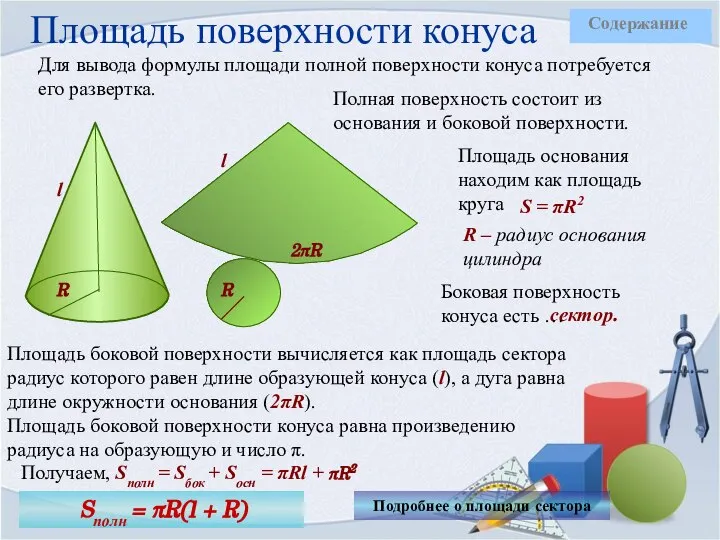
- 25. Площадь поверхности конуса Для вывода формулы площади полной поверхности конуса потребуется его развертка. Sполн = πR(l
- 26. Площадь сектора Вычисляя боковую поверхность конуса вписываем в данную формулу новые обозначения и выражаем α через
- 27. Решение устных задач с конусом 1)Во сколько раз увеличится боковая поверхность конуса, если его образующая увеличится
- 28. Решение задач 3) Коническая крыша башни имеет диаметр 6 м и высоту 2 м. сколько листов
- 29. Решение задач 4) Сколько м2 ткани потребуется для пошива шатра цирка «Шапито», если диаметр шатра составляет
- 30. Определение шара Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем
- 31. Сечения шара Сечение шара, проходящее через его центр. В сечении – Сечение плоскостью, не проходящей через
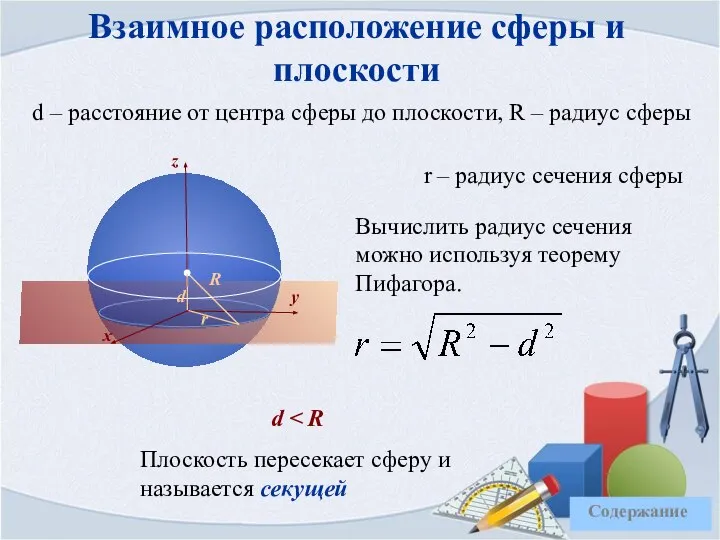
- 32. Взаимное расположение сферы и плоскости d – расстояние от центра сферы до плоскости, R – радиус
- 33. Взаимное расположение сферы и плоскости d – расстояние от центра сферы до плоскости, R – радиус
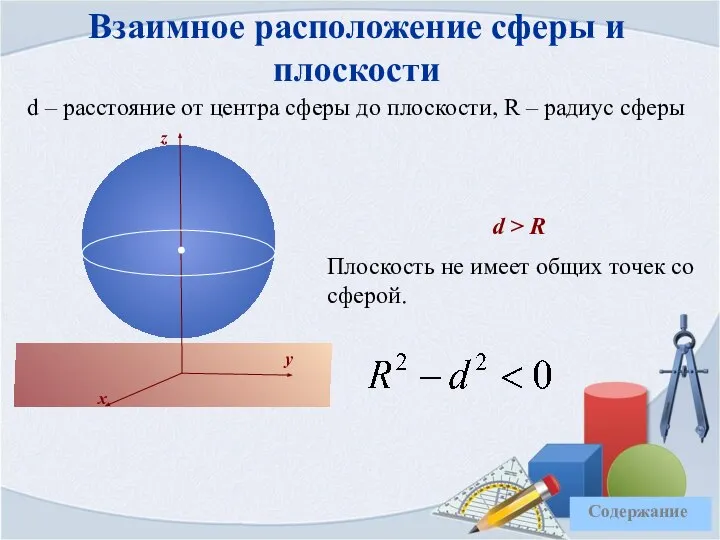
- 34. Взаимное расположение сферы и плоскости d – расстояние от центра сферы до плоскости, R – радиус
- 35. Решение задач 1)Вычислить площадь поверхности шара изображенного на рисунке. R = ОА, Найдем ОА из ΔАСО.
- 36. О - центр Земли, А – точка орбиты в которой находится корабль, В и С –
- 37. 1)Из справочник имеем длину дуги от экватора до полярного круга 66°. Этой же мере соответствует центральный
- 38. Географическая справка Географические широты могут иметь значение от 0° до 90°. Географическая широта 90° находится у
- 39. Благодарю Ранько Е. А. учителя начальных классов МАОУ лицей №21 г. Иваново за предоставленный шаблон презентации
- 40. Литература Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11: Учеб. для общеобразоват. учреждений. –
- 42. Скачать презентацию




























 Урок повторения и самоконтроля
Урок повторения и самоконтроля Презентация на тему Движение. Виды движения
Презентация на тему Движение. Виды движения  Пространственные и временные представления
Пространственные и временные представления Графики функций
Графики функций Статистическая радиотехника. Случайный процесс, ансамбль его реализаций
Статистическая радиотехника. Случайный процесс, ансамбль его реализаций Координаты на прямой
Координаты на прямой Интегрирование тригонометрических и иррациональных функций
Интегрирование тригонометрических и иррациональных функций Первый признак подобия треугольников. Решение задач
Первый признак подобия треугольников. Решение задач Понятие многогранника, призмы и их элементов
Понятие многогранника, призмы и их элементов Численные решения обыкновенных дифференциальных уравнений (ОДУ)
Численные решения обыкновенных дифференциальных уравнений (ОДУ) Графики функций. Устная работа
Графики функций. Устная работа Задачи на сложение и вычитание
Задачи на сложение и вычитание Презентация на тему Квадратное уравнение и его корни
Презентация на тему Квадратное уравнение и его корни  Случаи вычитания 11-
Случаи вычитания 11- Метр. (2класс)
Метр. (2класс) Эконометрика. Лекция 2
Эконометрика. Лекция 2 Провешивание прямой на местности
Провешивание прямой на местности Обыкновенные дроби
Обыкновенные дроби Теорема косинусов
Теорема косинусов Площадь параллелограмма
Площадь параллелограмма Анализ и синтез как методы научного познания, их применение при обучении математике
Анализ и синтез как методы научного познания, их применение при обучении математике Презентация на тему Арифметика Магницкого
Презентация на тему Арифметика Магницкого  Цилиндр. Цилиндры вокруг нас
Цилиндр. Цилиндры вокруг нас Кредиты в нашей жизни или элементы финансовой математики
Кредиты в нашей жизни или элементы финансовой математики Построение графика квадратичной функции
Построение графика квадратичной функции Многоугольники. Виды многоугольников
Многоугольники. Виды многоугольников Деление окружности на 5 равных частей. Сопряжение
Деление окружности на 5 равных частей. Сопряжение Логарифм числа и его свойства
Логарифм числа и его свойства