Презентация на тему Метод областей

Выдающийся французский математик, физик и писатель, один из создателей математического анализа, проектной геометрии, теории вероятностей, гидростатики, создатель механического счетного устройства – «паскалева колеса» и наконец философ, чьи мысли оказывали влияние на многих выдающихся людей сказал:
Блэз Паскаль
Blaise Pascal
(19.06.1623 – 19.08.1662)

«Предмет математики настолько серьёзен, что надо не упускать случая сделать его занимательным»
«Крупное научное открытие даёт решение крупной проблемы , но и в решении любой задачи присутствует крупица открытия»

Гипотеза:
можно ли, очень удобный метод интервалов для решения рациональных неравенств, применить при решении неравенств с параметрами?

ХОД РАБОТЫ:
Постановка целей исследования;
Изучение материала по теме «Метод областей»;
Решение простейших неравенств и их систем изучаемым методом;
Решение систем неравенств с параметром из сборника тренировочных заданий ЕГЭ;
Создание презентации и оформление буклета;
Подведение итогов работы.

ВВЕДЕНИЕ
Для успешного исследования многих задач повышенной сложности полезно уметь строить не только графики функций, но и множества точек плоскости, координаты которых удовлетворяют заданным уравнениям, неравенствам или их системам. Эффективно строить на координатной плоскости такие множества позволяет метод областей. Это весьма полезный прием можно назвать обобщающим методом интервалов.

Метод областей особенно полезен при решении уравнений или неравенств с параметром. Применение метода интервалов в таких случаях затруднено, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра. Это означает необходимость сравнивать их между собой и рассматривать различные случаи. В этой ситуации нам может помочь метод областей.

ЦЕЛЬ РАБОТЫ:
Познакомиться с новым методом решения неравенств и их систем в рамках подготовки к сдаче ЕГЭ.

ЗАДАЧИ ИССЛЕДОВАНИЯ:
Рассмотреть «метод областей» как общий прием решения неравенств на плоскости;
Применить «метод областей» к решению задач с параметрами.
Показать типы задач, которые могут быть решены с помощью данного метода.

УКАЗАТЬ МНОЖЕСТВО ТОЧЕК ПЛОСКОСТИ (Х; У), УДОВЛЕТВОРЯЮЩИХ НЕРАВЕНСТВУ:
Рассмотрим
f(х;у)=х(у-х)(у+х)
f(х;у)=0, если
у-х=0
у+х=0
или
у=х
у=-х
х=0
или
1)

Заметим, что все прямые «порождены» сомножителями, входящими в функцию f(x) нечетным образом, и при переходе через любую из указанных трех прямых происходит смена знака этой функции. Поэтому в других областях знаки функции f(x) вычислять не требуется.
f(1;0)=1∙(0-1)∙(0+1)=-1<0

2)
Рассмотрим
f(х;у)=
f(х;у)=0, если
или
у-х=0
или
у+х=0
у=х
у=-х
у=х
у=-х
х=0

у=х
у=-х
В отличии от примера 1 при переходе через прямую х=0 знак функции не меняется, так как соответствующий ей сомножитель входит в выражение для у=f(x) четным образом. (Как в случае кратных корней при решении неравенств методом интервалов)
f(1;0)=12∙(0-1)∙(0+1)=-1<0

Преобразуем неравенство:
Рассмотрим f(х;у)=
f(х;у)=0, если у=0;
f(х;у) не существует,
если х-у=0, если у=х;
f(0;1)=
3)
у=х
у=0

f(х;у)=
f(х;у)=0, если
х-у=0 или
у=х
f(1;0)=(1-0)∙(1-02 +1)=2>0
4)
Рассмотрим
у=х

Решение систем неравенств с параметром
«Методом областей»

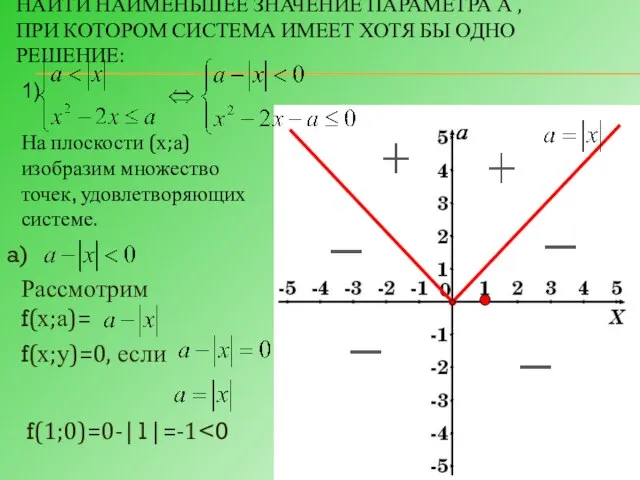
НАЙТИ НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ПАРАМЕТРА А , ПРИ КОТОРОМ СИСТЕМА ИМЕЕТ ХОТЯ БЫ ОДНО РЕШЕНИЕ:
На плоскости (х;а)
изобразим множество
точек, удовлетворяющих
системе.
а)
Рассмотрим
f(х;а)=
f(х;у)=0, если
f(1;0)=0-|1|=-1<0
1)

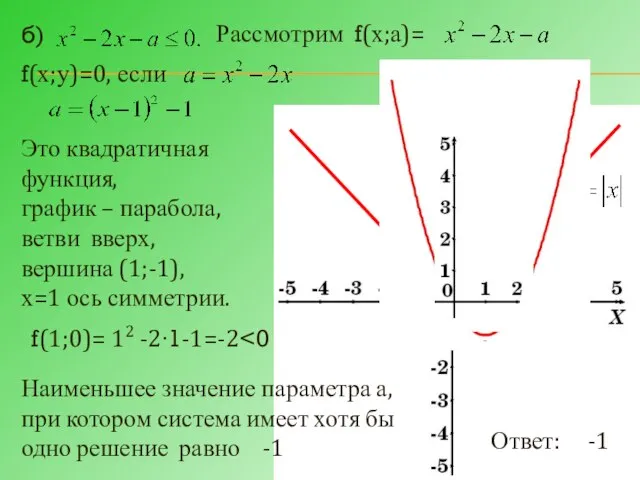
б)
Рассмотрим f(х;а)=
f(х;у)=0, если
f(1;0)= 12 -2∙1-1=-2<0
Это квадратичная функция,
график – парабола,
ветви вверх,
вершина (1;-1),
х=1 ось симметрии.
Наименьшее значение параметра а, при котором система имеет хотя бы одно решение равно -1
Ответ: -1

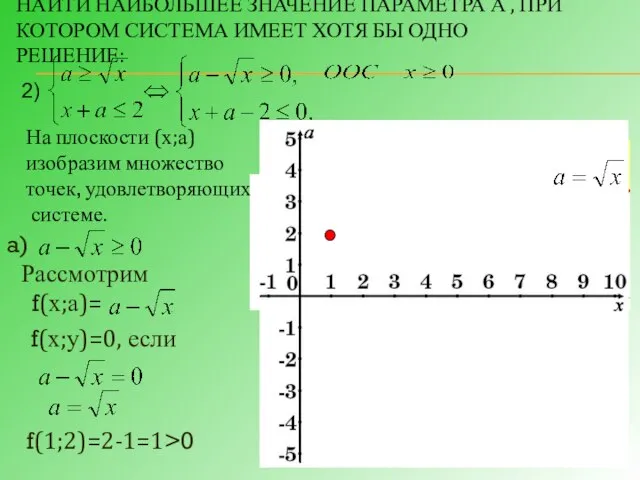
НАЙТИ НАИБОЛЬШЕЕ ЗНАЧЕНИЕ ПАРАМЕТРА А , ПРИ КОТОРОМ СИСТЕМА ИМЕЕТ ХОТЯ БЫ ОДНО РЕШЕНИЕ:
На плоскости (х;а) изобразим множество
точек, удовлетворяющих
системе.
а)
Рассмотрим
f(х;а)=
f(х;у)=0, если
f(1;2)=2-1=1>0
2)

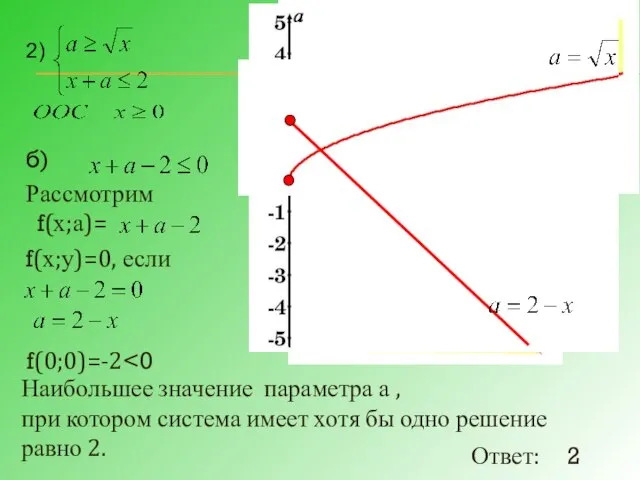
б)
Рассмотрим
f(х;а)=
f(х;у)=0, если
f(0;0)=-2<0
Наибольшее значение параметра а ,
при котором система имеет хотя бы одно решение равно 2.
Ответ: 2
2)

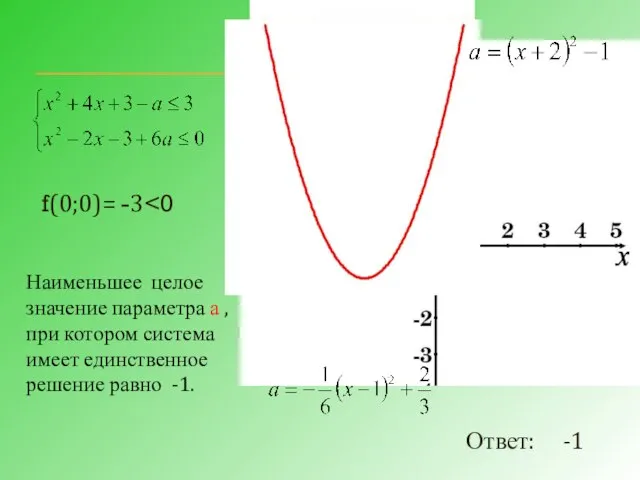
Найти наименьшее целое значение
параметра а , при котором система имеет единственное решение:
3)

Преобразуем систему:
1) Рассмотрим f(х;а)=
f(х;у)=0, если
Это квадратичная функция, график – парабола,
ветви вверх, вершина (-2;-1), х=-2 ось симметрии.

f(0;0)= 3>0

2)Рассмотрим f(х;а)=
f(х;у)=0, если
Это квадратичная функция, график – парабола,
ветви вниз, вершина (1; ), х=1ось cимметрии.

f(0;0)= -3<0
Наименьшее целое
значение параметра а ,
при котором система
имеет единственное решение равно -1.
Ответ: -1

Готовимся к ЕГЭ!

НАЙДИТЕ ВСЕ ЗНАЧЕНИЯ А , ПРИ КАЖДОМ ИЗ КОТОРЫХ ОБЩИЕ РЕШЕНИЯ НЕРАВЕНСТВ И ОБРАЗУЮТ НА ЧИСЛОВОЙ ОСИ ОТРЕЗОК ДЛИНЫ ЕДИНИЦА.
а)
Решение:
Найдем а, при которых система неравенств (1) имеет решения:
Преобразуем систему:

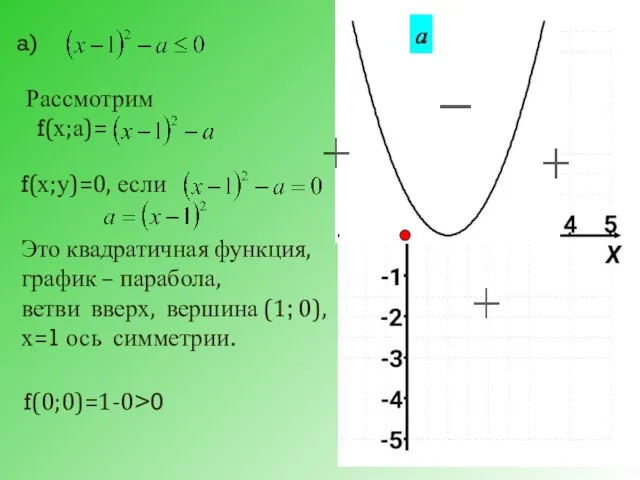
а)
Рассмотрим
f(х;а)=
f(х;у)=0, если
Это квадратичная функция,
график – парабола,
ветви вверх, вершина (1; 0),
х=1 ось симметрии.
f(0;0)=1-0>0

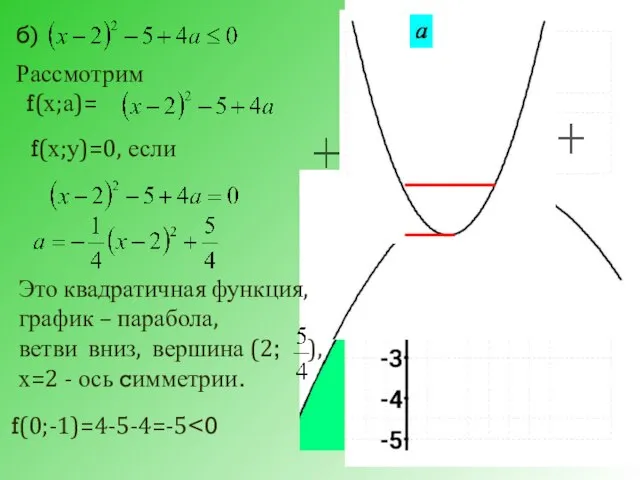
б)
Рассмотрим
f(х;а)=
f(х;у)=0, если
Это квадратичная функция,
график – парабола,
ветви вниз, вершина (2; ),
х=2 - ось cимметрии.
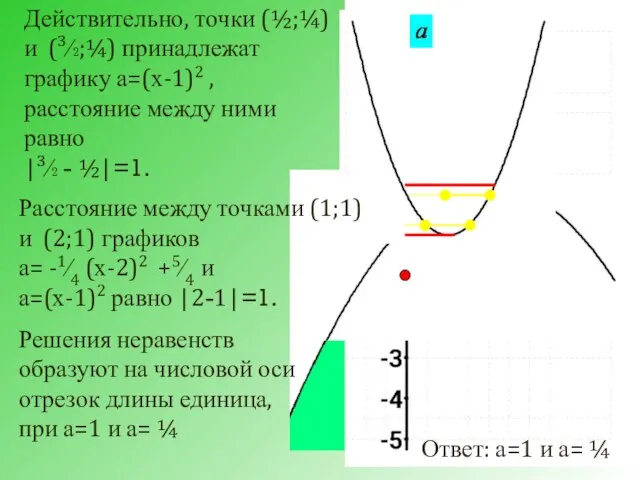
f(0;-1)=4-5-4=-5<0

Система неравенств имеет решение,
если aϵ [0; ].
Решения неравенств
образуют на числовой оси отрезок длины единица,
при а=1 и а= ¼
а=1
а= ¼

Действительно, точки (½;¼) и (³∕₂;¼) принадлежат графику а=(х-1)2 , расстояние между ними равно
|³∕₂ - ½|=1.
Решения неравенств
образуют на числовой оси отрезок длины единица,
при а=1 и а= ¼
Ответ: а=1 и а= ¼
Расстояние между точками (1;1) и (2;1) графиков
а= -1∕4 (х-2)2 +5∕4 и
а=(х-1)2 равно |2-1|=1.

Метод областей можно назвать
методом интервалов для плоскости.
Его можно использовать
для решения заданий ЕГЭ части С .
Таким образом:

Проверь себя!

Системы неравенств с параметрами

ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА «А» , СИСТЕМА ИМЕЕТ ЕДИНСТВЕННОЕ РЕШЕНИЕ:
Найти наименьшее значение параметра «а» ,при котором система имеет хотя бы одно решение:

НАЙТИ НАИМЕНЬШЕЕ ЦЕЛОЕ ЗНАЧЕНИЕ ПАРАМЕТРА «А» ,ПРИ КОТОРОМ СИСТЕМА ИМЕЕТ ХОТЯ БЫ ОДНО РЕШЕНИЕ:
Найти наибольшее значение параметра «а» ,при котором система имеет хотя бы одно решение:

Найти наибольшее целое значение параметра «а» ,при котором система имеет хотя бы одно решение:

Замечание: метод областей как таковой – лишь иллюстрация. Решение может считаться обоснованным, только если получены и выписаны уравнения всех линий, изображенных на рисунке, и приведены доказательства правильности расстановки знаков. Рисунок, естественно, должен быть выполнен по возможности аккуратнее. В частности, желательно указать, какие линии входят в рассматриваемое множество, а какие нет.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.
Математика для поступающих в серьезные вузы.
О.Ю.Черкасов , А.Г.Якушев . – M.: Московский лицей, 2009.
ЕГЭ 2010 математика. Федеральный институт педагогических измерений. Официальный разработчик контрольных измерительных материалов для ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА.
Общая редакция: А.Л.Семенов, И.В.Ященко.