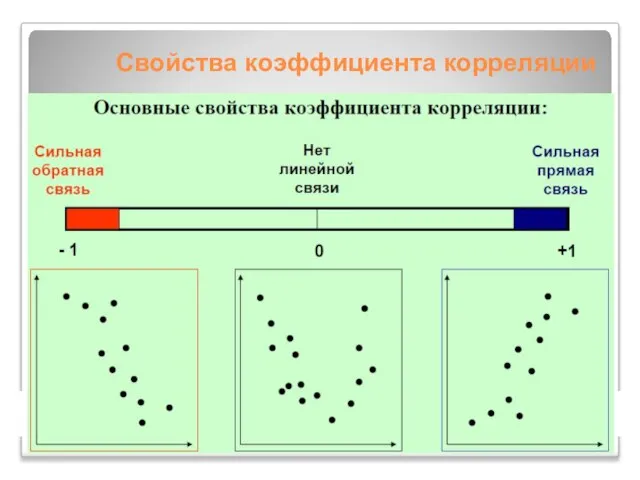
Слайд 4Свойства коэффициента корреляции
Слайд 6Построение уравнения регрессии

Слайд 7
Чаще всего используются следующие зависимости :
линейная ;
параболическая ;
экспоненциальная .
Оценка параметров осуществляется

методом наименьших квадратов:
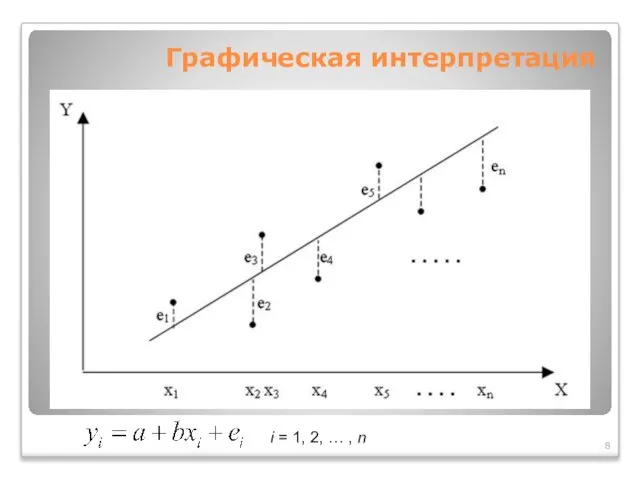
Слайд 8Графическая интерпретация
i = 1, 2, … , n
Слайд 12Алгоритм кластерного анализа: K-means
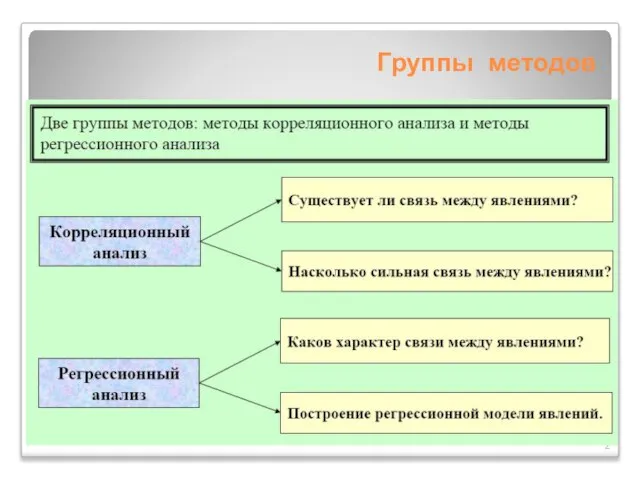
Одной из широко используемых методик кластеризации является разделительная

кластеризация, в соответствии с которой для выборки данных, содержащей n записей, задаётся число кластеров k, которое должно быть сформировано. Затем алгоритм разбивает все объекты выборки на k групп (k К наиболее простым и эффективным алгоритмам кластеризации относится k-means (k-средних). Он состоит из четырёх шагов:
1. Задаётся число кластеров k, которое должно быть сформировано из объектов исходной выборки.
2. Случайным образом выбирается k записей, которые будут служить начальными центрами кластеров.
3. Для каждой записи исходной выборки определяется ближайший к ней центр кластера.
4. Производится вычисление центроидов - центров тяжести кластеров. Это делается путём определения среднего для значений каждого признака всех записей в кластере.
Шаги 3 и 4 повторяются до тех пор, пока не будет выполнено условие в соответствии с некоторым критерием сходимости (чаще всего используется сумма квадратов ошибок между центроидом кластера и всеми вошедшими в него записями).
Остановка алгоритма производится, когда на каждой итерации в каждом кластере остаётся один и тот же набор записей.









 Параллельные плоскости
Параллельные плоскости Приёмы умножения на 2
Приёмы умножения на 2 Математика 4 класс
Математика 4 класс Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Математика в профессии Застройщик
Математика в профессии Застройщик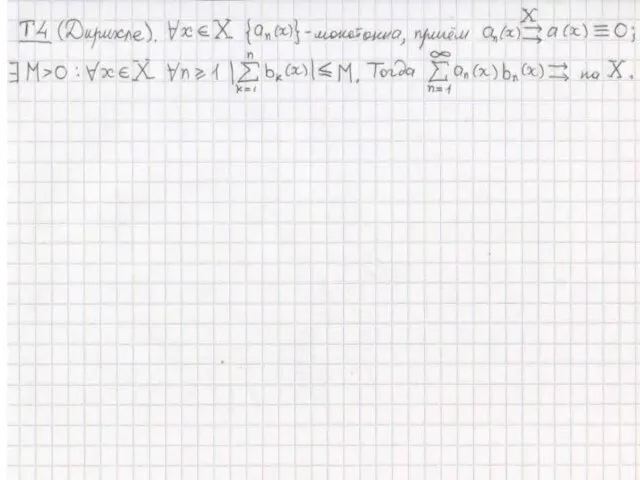 Свойства равномерно-сходящихся плоскостей и рядов
Свойства равномерно-сходящихся плоскостей и рядов Презентация на тему Пропорции
Презентация на тему Пропорции  Перетворення графіків
Перетворення графіків Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Тренажёр. Единицы измерения
Тренажёр. Единицы измерения Обыкновенные дроби
Обыкновенные дроби Устная работа. Вычисления
Устная работа. Вычисления Вычисление реакций и перемещений в статически неопределимых системах
Вычисление реакций и перемещений в статически неопределимых системах Перпендикулярные прямые
Перпендикулярные прямые Функциональная грамотность (математика) - задачи
Функциональная грамотность (математика) - задачи Решение тригонометрических уравнений
Решение тригонометрических уравнений Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10
Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10 Сложение отрицательных чисел
Сложение отрицательных чисел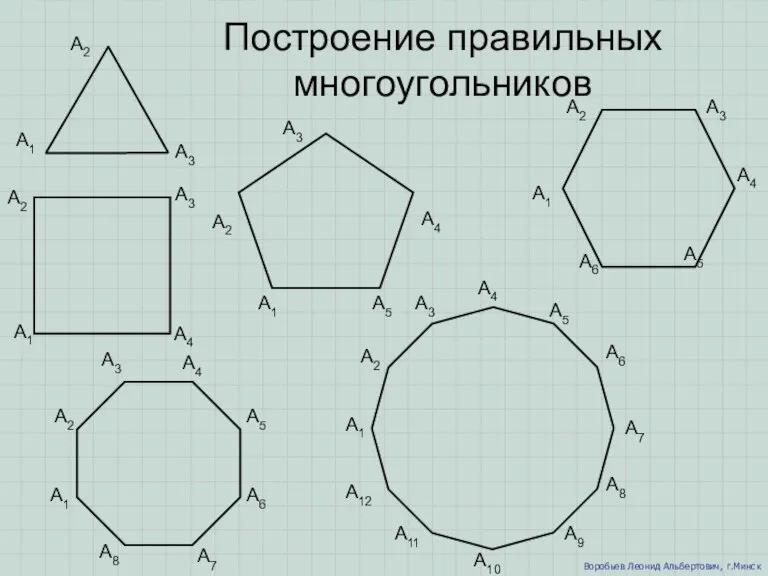 Построение правильных многоугольников
Построение правильных многоугольников Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Золотое сечение. Витрувий
Золотое сечение. Витрувий Презентация на тему Кто хочет стать математиком
Презентация на тему Кто хочет стать математиком  Решение логарифмических уравнений к занятию
Решение логарифмических уравнений к занятию Понятие и виды средних величин
Понятие и виды средних величин Презентация на тему Вклад Пифагора в развитие музыки 7 класс
Презентация на тему Вклад Пифагора в развитие музыки 7 класс  Квадратные неравенства с параметрами
Квадратные неравенства с параметрами Логарифм и его свойства
Логарифм и его свойства