Содержание
- 2. Теорема Фалеса Геометрия 8 класс
- 3. Фалес Милетский «Отец философии» 624 до н.э – 548 до н.э.
- 4. Считается, что именно Фалес «привез» геометрию из Египта и познакомил с ней греков. Его деятельность привлекла
- 5. Легенда рассказывает о том, что Фалес, будучи в Египте, поразил фараона Амасиса тем, что сумел точно
- 6. Есть одна точная дата, связанная с жизнью Фалеса, — 585 до н. э., когда в Милете
- 7. Но одна из важнейших заслуг Фалеса в том, что ему приписываются многие геометрические теоремы круг делится
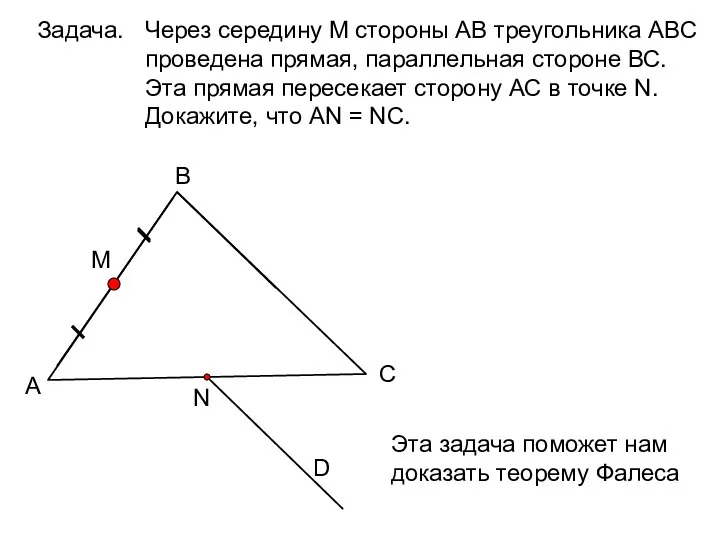
- 8. Задача. А В С D Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне
- 9. Теорема: если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они
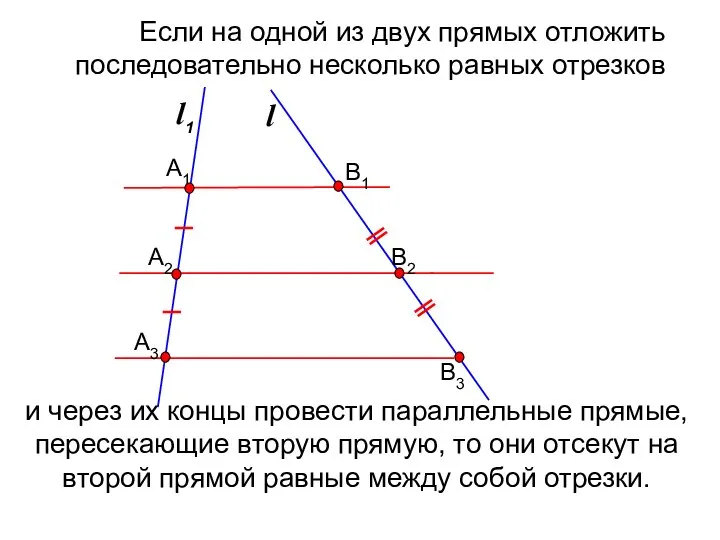
- 11. Фалес Милетский Древнегреческий ученый (ок. 625 – 547 гг. до н. э.) Теорема Фалеса Если на
- 12. l1 l и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на
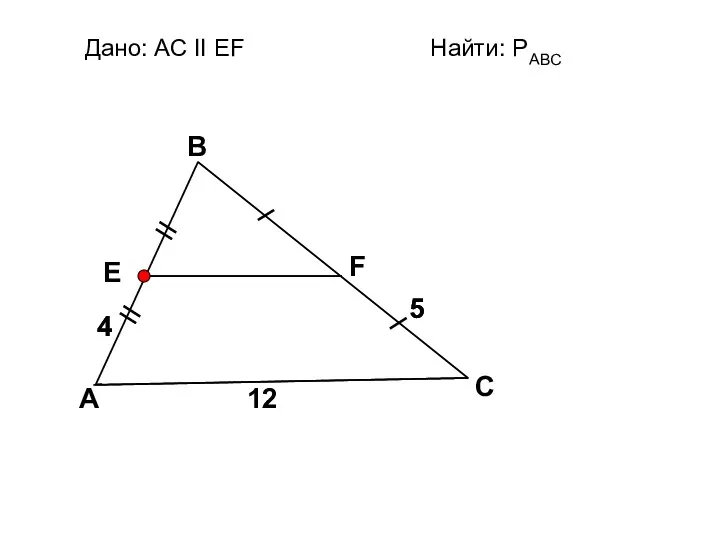
- 13. A B C F E Дано: АС II EF Найти: PАВС 12 5 5 4 4
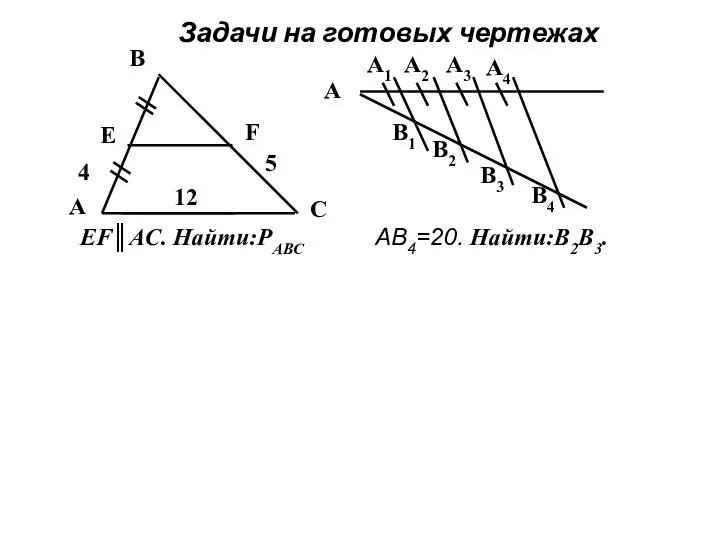
- 14. Задачи на готовых чертежах A B C E F 4 5 12 EF║AC. Найти:РАВС A A1
- 15. ЗАДАЧА: РАЗДЕЛИТЕ ДАННЫЙ ОТРЕЗОК НА n РАВНЫХ ЧАСТЕЙ А В 1.Проведём из точки А луч АО,
- 16. Средняя линия треугольника Тема урока:
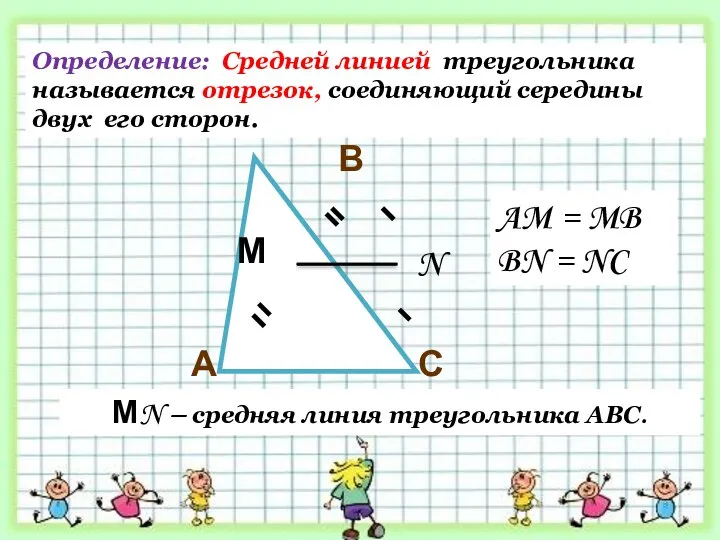
- 17. С В А М N МN – средняя линия треугольника АВС. Определение: Средней линией треугольника называется
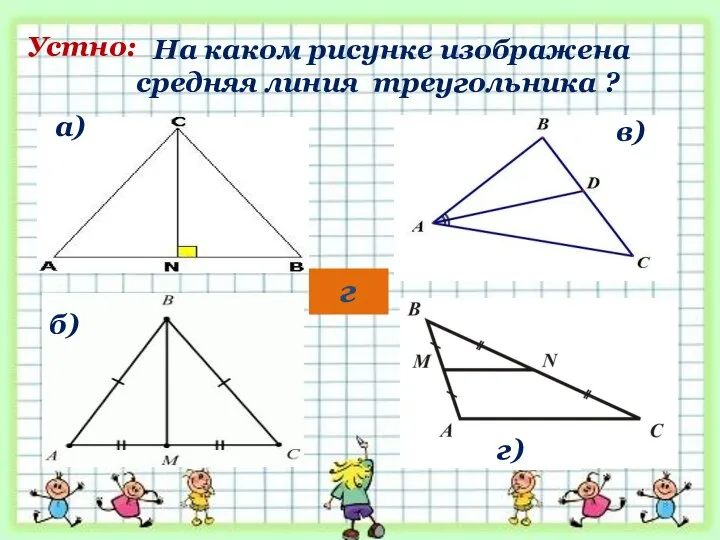
- 18. На каком рисунке изображена средняя линия треугольника ? а) г) б) в) Устно: г
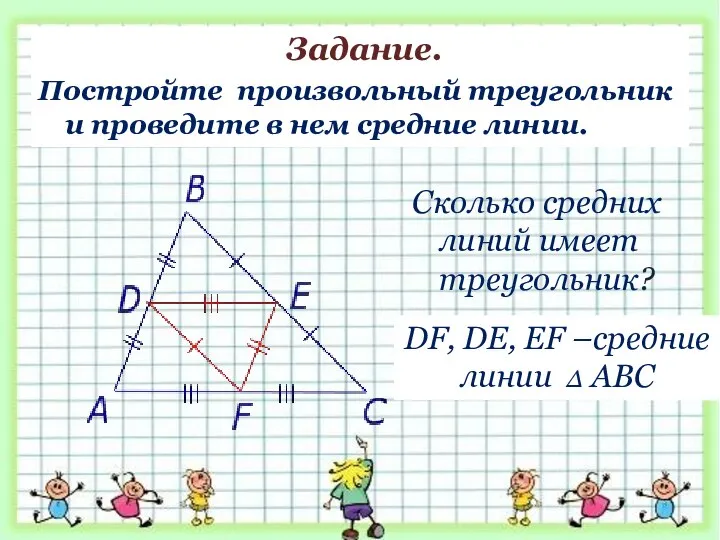
- 19. Сколько средних линий имеет треугольник? Задание. Постройте произвольный треугольник и проведите в нем средние линии. DF,
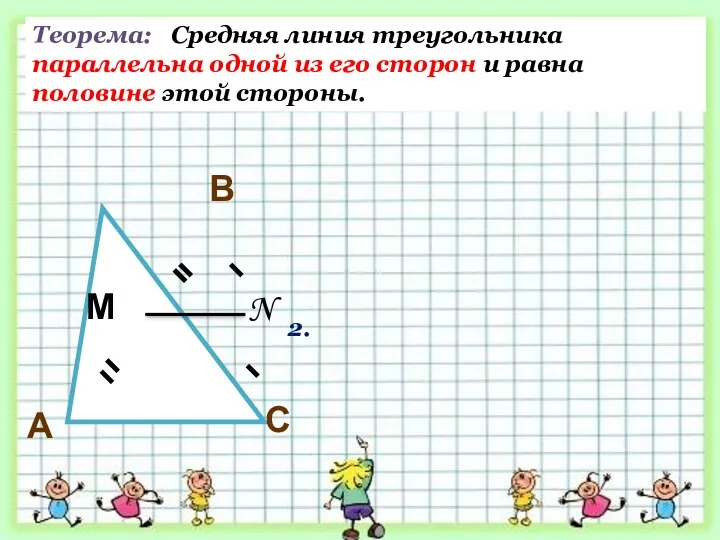
- 20. Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. С В
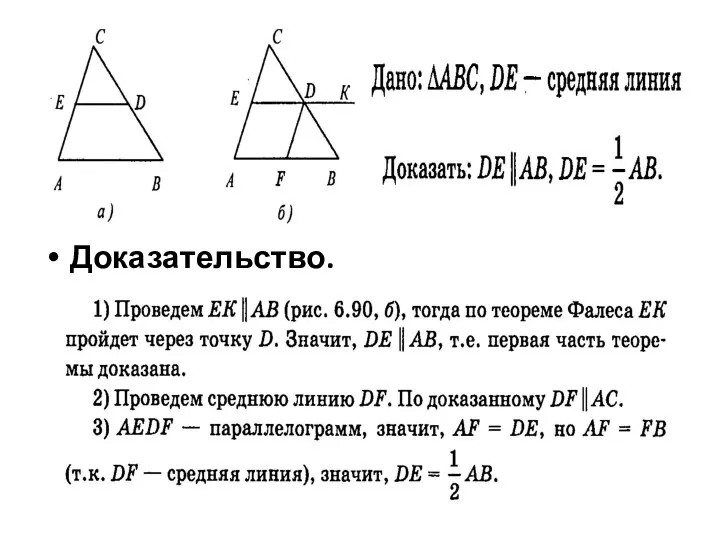
- 21. Доказательство.
- 22. 1. Сколько треугольников вы видите? 2. Есть ли равные треугольники? Почему? Устно: 3. Сколько параллелограммов на
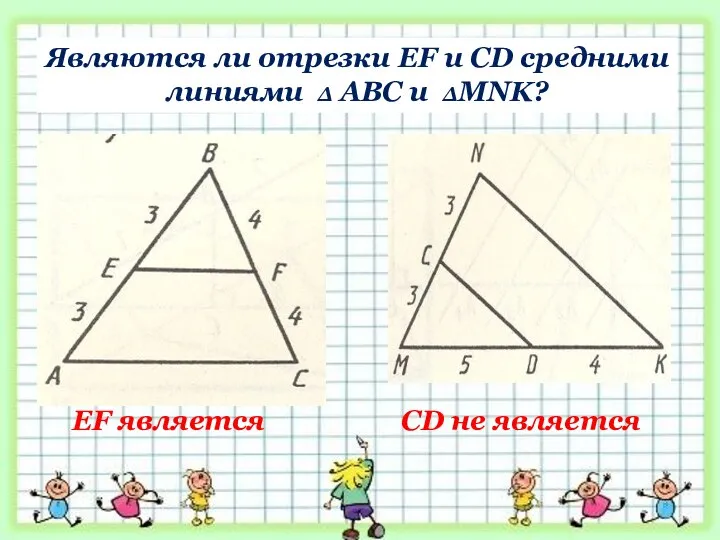
- 23. Являются ли отрезки EF и CD средними линиями ∆ АВС и ∆MNK? EF является CD не
- 24. Отрезок MN является средней линией треугольника … в)
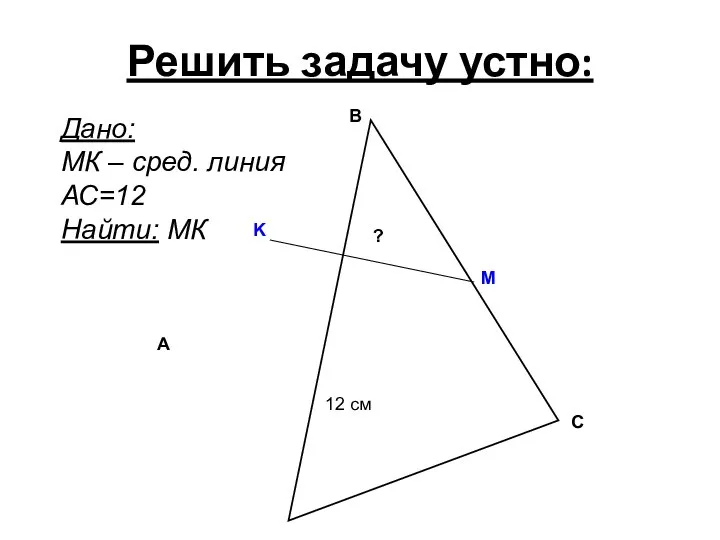
- 25. Решить задачу устно: A B C K M 12 см Дано: MК – сред. линия АС=12
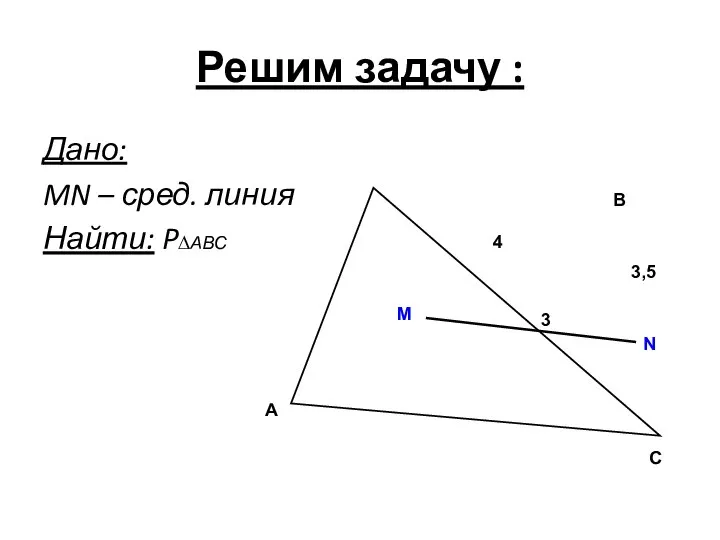
- 26. Решим задачу : Дано: MN – сред. линия Найти: P∆АВС M N A B C 3
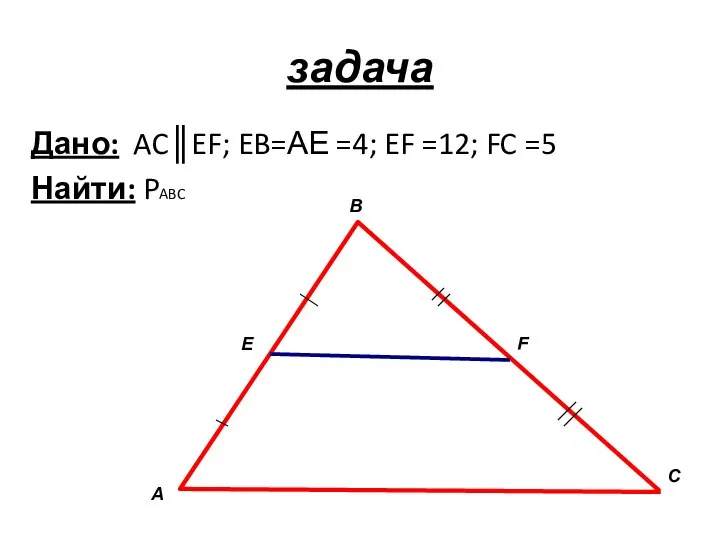
- 27. задача Дано: AC║EF; EB=АЕ =4; EF =12; FC =5 Найти: PABC А В С E F
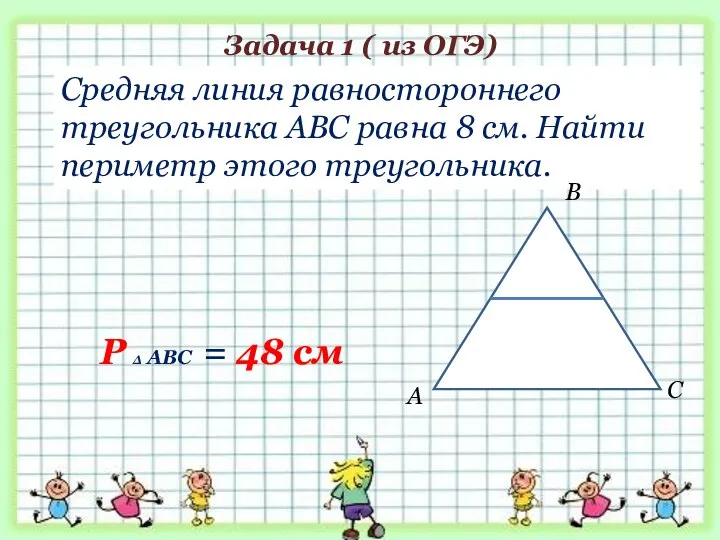
- 28. Задача 1 ( из ОГЭ) Средняя линия равностороннего треугольника АВС равна 8 см. Найти периметр этого
- 29. 2 урок
- 30. A B C M Дано: S∆ABC = 40 см² Найти: SΔMNK K N Задача 2 SΔ
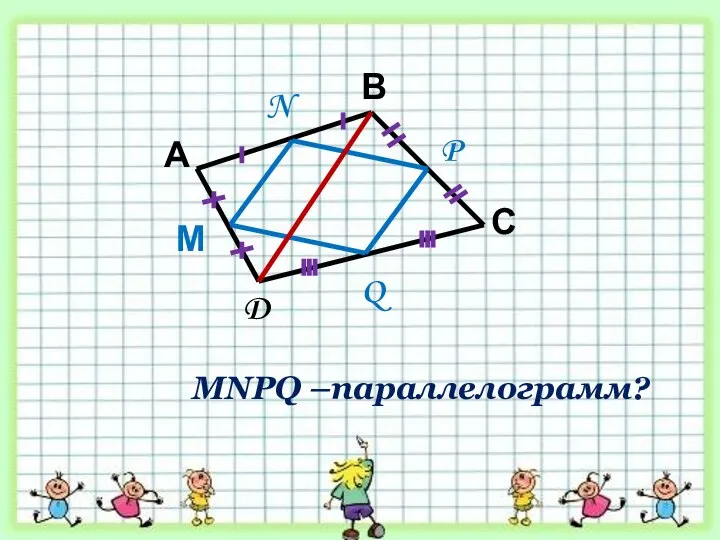
- 31. А В С D М N P Q MNPQ –параллелограмм?
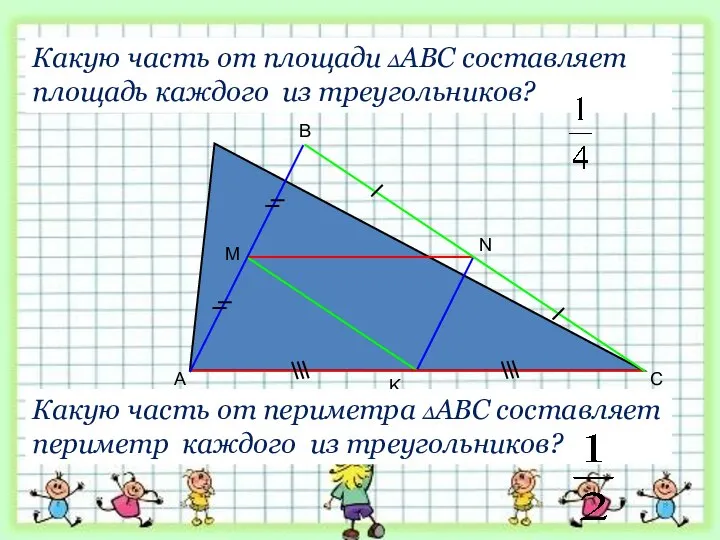
- 32. A B C M K N Какую часть от площади ∆АВС составляет площадь каждого из треугольников?
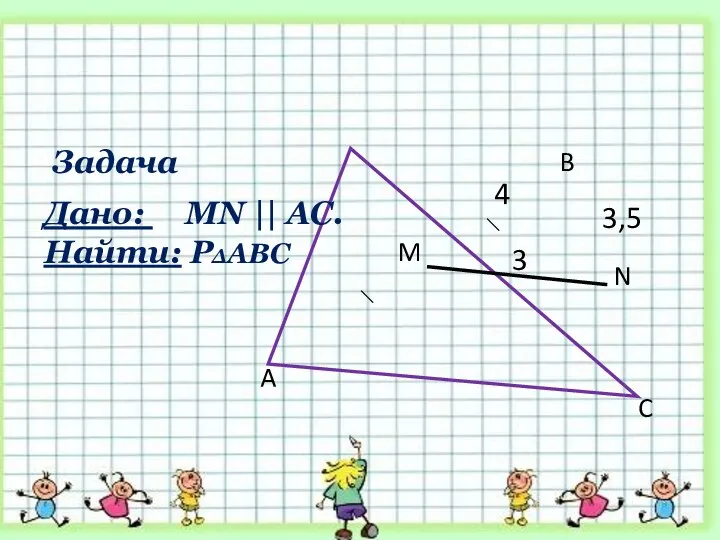
- 33. Задача 3,5 A B C N M 3 4 Дано: MN || AC. Найти: Р∆АВС
- 34. Какие новые знания получены на уроке? Что называют средней линией треугольника? Сформулируйте теорему о средней линии
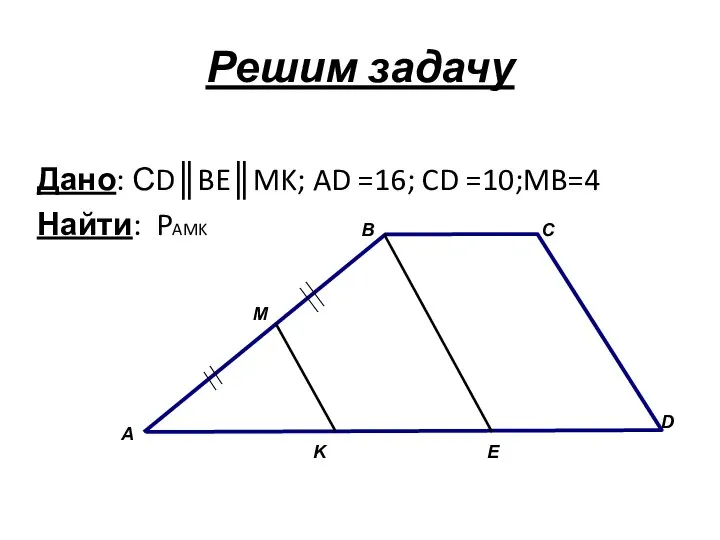
- 35. Решим задачу Дано: СD║BE║MK; AD =16; CD =10;MB=4 Найти: PAMK А B C D E K
- 36. Моё настроение Отличное! Все понятно! Непонятное! Есть над чем подумать…
- 38. Скачать презентацию
















 Длиннее, короче. Одинаковые по длине
Длиннее, короче. Одинаковые по длине Функция y=k/x, её график и свойства. 8 класс. Урок 2
Функция y=k/x, её график и свойства. 8 класс. Урок 2 Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Письмо цифр
Письмо цифр Применение математики в нематематических областях
Применение математики в нематематических областях Четырёхугольники (повторение материала)
Четырёхугольники (повторение материала) Презентация на тему Леонтий Филиппович Магницкий
Презентация на тему Леонтий Филиппович Магницкий  Геометрия вокруг нас
Геометрия вокруг нас Окружность. Углы
Окружность. Углы Практическое занятие №7 Минимизация логического автомата
Практическое занятие №7 Минимизация логического автомата ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции
ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции Дифференциальные уравнения в частных производных
Дифференциальные уравнения в частных производных Веселая математика
Веселая математика Фрагмент урока по методике преподавания математики
Фрагмент урока по методике преподавания математики Сложение и вычитание чисел в пределах 20
Сложение и вычитание чисел в пределах 20 Кривые как траектории движения точек
Кривые как траектории движения точек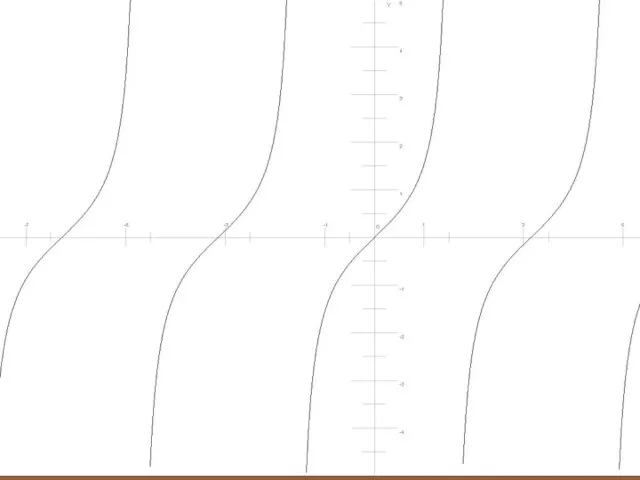 Преобразования графиков функций
Преобразования графиков функций Свойства монотонных функций
Свойства монотонных функций Презентация на тему Построение сечений многогранников методом «следа»
Презентация на тему Построение сечений многогранников методом «следа»  Теория множеств
Теория множеств Координатные векторы
Координатные векторы Решение задач на проценты, растворы и сплавы
Решение задач на проценты, растворы и сплавы Знакомство с линиями чертежа Замкнутая, незамкнутая
Знакомство с линиями чертежа Замкнутая, незамкнутая Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы
Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы Параллельность прямой и плоскости
Параллельность прямой и плоскости Ряды. Сходимость рядов
Ряды. Сходимость рядов