- Главная
- Математика
- Вторая производная, ее физический смысл. Применение производной к построению графиков функций

Содержание
Слайд 2 Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x0 ), то её производная называется второй производной функции f ( x ) в
Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x0 ), то её производная называется второй производной функции f ( x ) в
точке ( x0 ), и обозначается f '' ( x0 ).
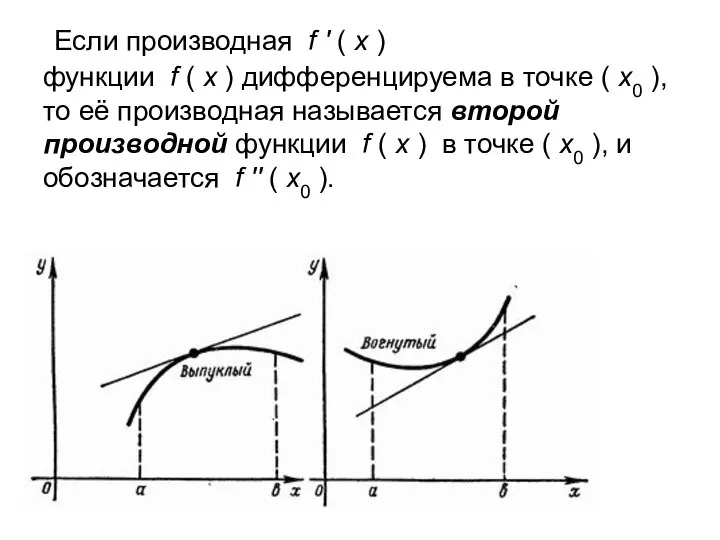
Слайд 3Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной
Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной

к кривой y = f ( x ) в любой точке ( x0 , f ( x0 )), x0 ( a, b ).
Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 )), x0 ( a, b ).
если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 )), x0 ( a, b ).
если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
Слайд 4Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.

 Проценты. Графический диктант
Проценты. Графический диктант Презентация на тему СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
Презентация на тему СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ  Функциональная грамотность: формирование, диагностика
Функциональная грамотность: формирование, диагностика Презентация по математике "Чтение и запись натуральных чисел. Разряд" -
Презентация по математике "Чтение и запись натуральных чисел. Разряд" -  Математика. Зачем она нам в жизни
Математика. Зачем она нам в жизни Рациональные дроби. 8 класс
Рациональные дроби. 8 класс Решение логарифмических уравнений к занятию
Решение логарифмических уравнений к занятию Презентация на тему Геометрические построения с помощью циркуля и линейки
Презентация на тему Геометрические построения с помощью циркуля и линейки  Знаки препинания в сложном предложении
Знаки препинания в сложном предложении Математические шифровки
Математические шифровки Область определения функции. С/Р
Область определения функции. С/Р Корни уравнения
Корни уравнения Возмущения линейных систем и проматрицы
Возмущения линейных систем и проматрицы 1665470218901_Лекция Бернулли-1
1665470218901_Лекция Бернулли-1 Сфера и шар
Сфера и шар Площади. Тест 8 класс
Площади. Тест 8 класс Многочлен. Основные понятия
Многочлен. Основные понятия Вынесение множителя из - под знака корня. Внесение множителя под знак корня
Вынесение множителя из - под знака корня. Внесение множителя под знак корня Модели решения функциональных и вычислительных задач. Методы и технологии моделирования
Модели решения функциональных и вычислительных задач. Методы и технологии моделирования Состав числа 10
Состав числа 10 Задачи на готовых чертежах. Подобные треугольники
Задачи на готовых чертежах. Подобные треугольники Измерение углов
Измерение углов Планы второго порядка
Планы второго порядка Метод неопределенных коэффициентов. Теорема о рациональном корне многочлена с целыми коэффициентами
Метод неопределенных коэффициентов. Теорема о рациональном корне многочлена с целыми коэффициентами Решение задач с уравнением реакции
Решение задач с уравнением реакции Соотношение между сторонами и углами треугольника. Скалярное произведение векторов. (Вариант 2)
Соотношение между сторонами и углами треугольника. Скалярное произведение векторов. (Вариант 2) Нахождение числа по его дроби. Урок-игра Детективное агентство
Нахождение числа по его дроби. Урок-игра Детективное агентство Игра Верю - не верю
Игра Верю - не верю