Содержание
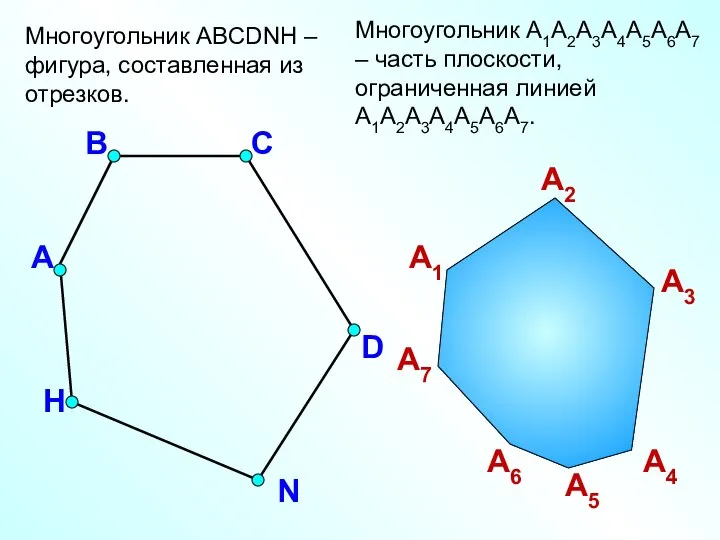
- 2. Многоугольник ABCDNH – фигура, составленная из отрезков. А В С D H N
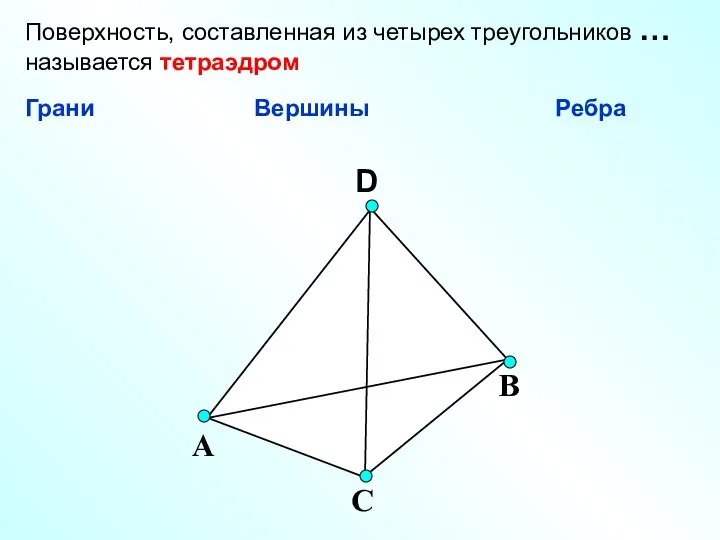
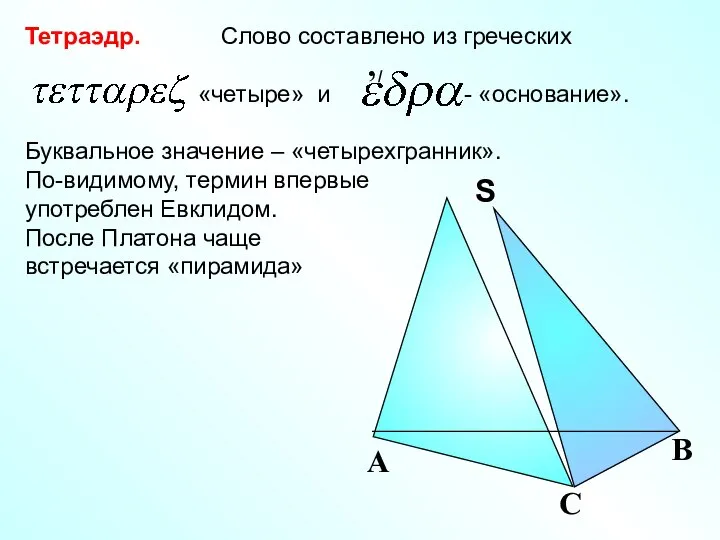
- 3. D А С В Поверхность, составленная из четырех треугольников … называется тетраэдром Грани Вершины Ребра
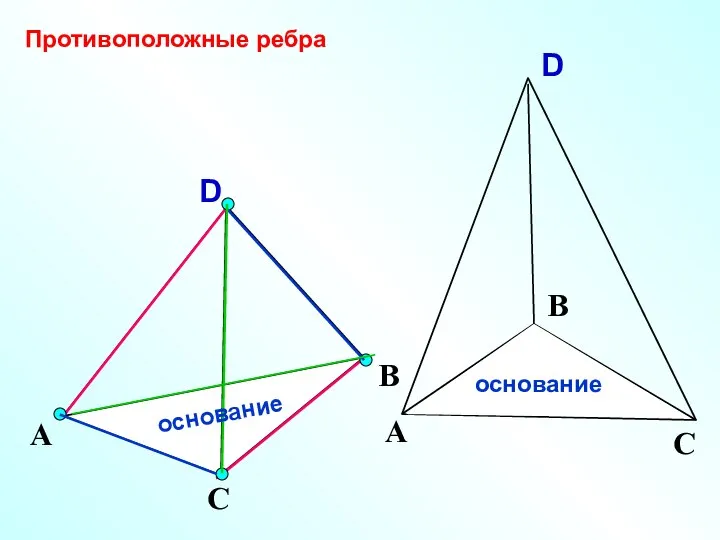
- 5. D А С В Противоположные ребра основание основание
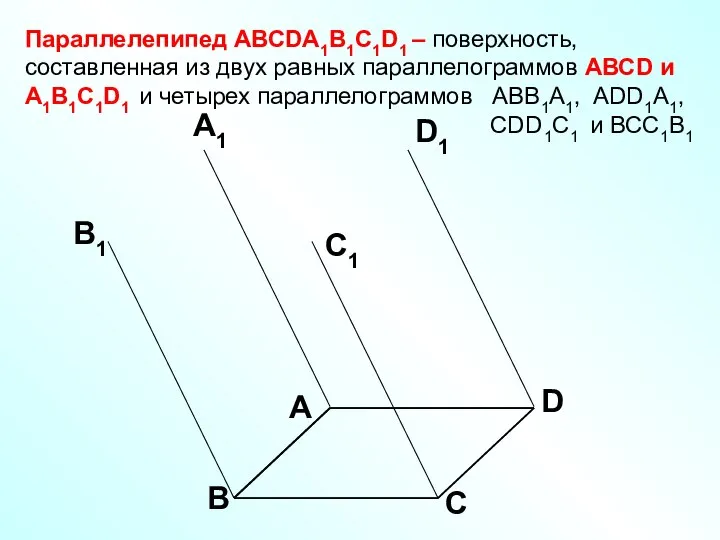
- 6. Параллелепипед АВСDA1B1C1D1 – поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1 и четырех параллелограммов АВВ1А1,
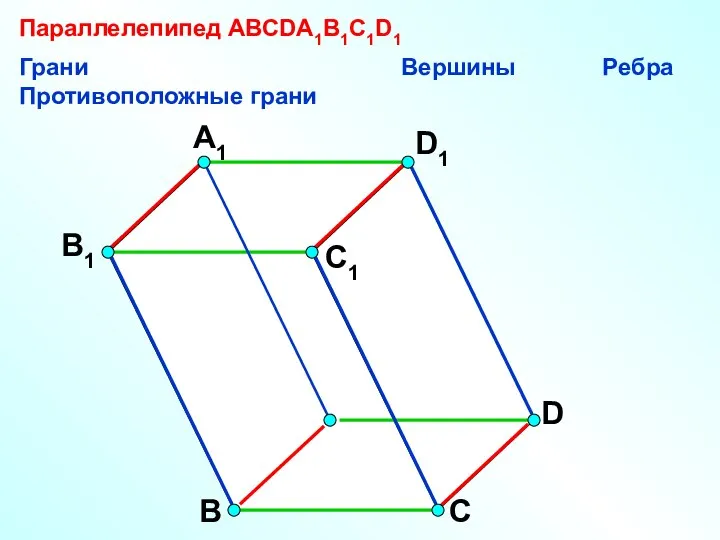
- 7. А В С D D1 С1 A1 B1 Параллелепипед АВСDA1B1C1D1 Грани Вершины Ребра Противоположные грани
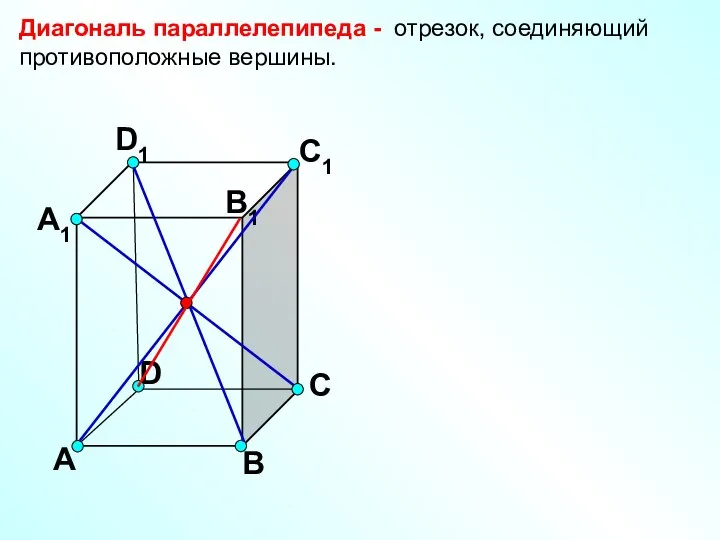
- 9. А В С D А1 D1 С1 B1 Диагональ параллелепипеда - отрезок, соединяющий противоположные вершины.
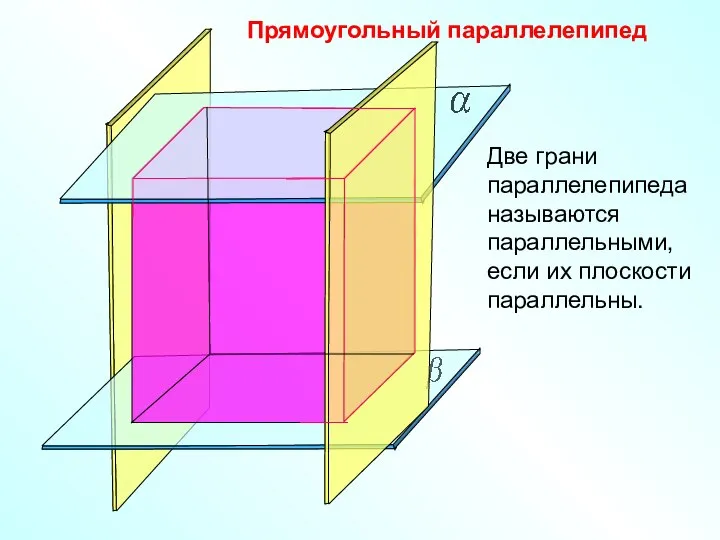
- 10. Прямоугольный параллелепипед Две грани параллелепипеда называются параллельными, если их плоскости параллельны.
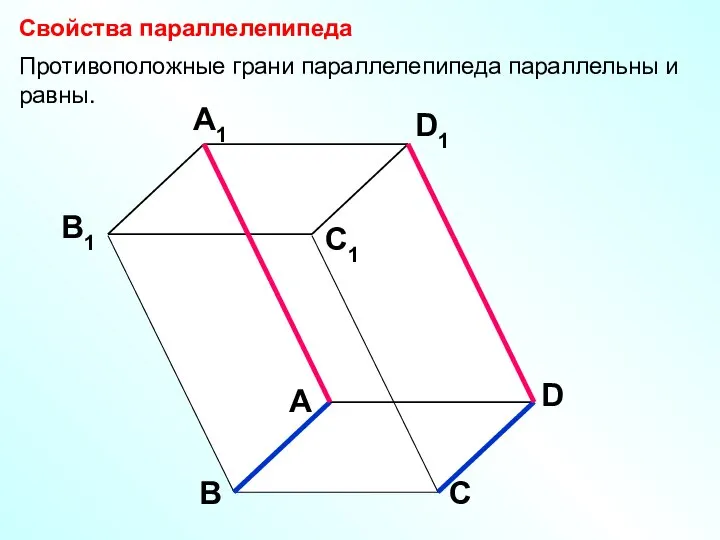
- 11. А В С D D1 С1 A1 B1 Свойства параллелепипеда Противоположные грани параллелепипеда параллельны и равны.
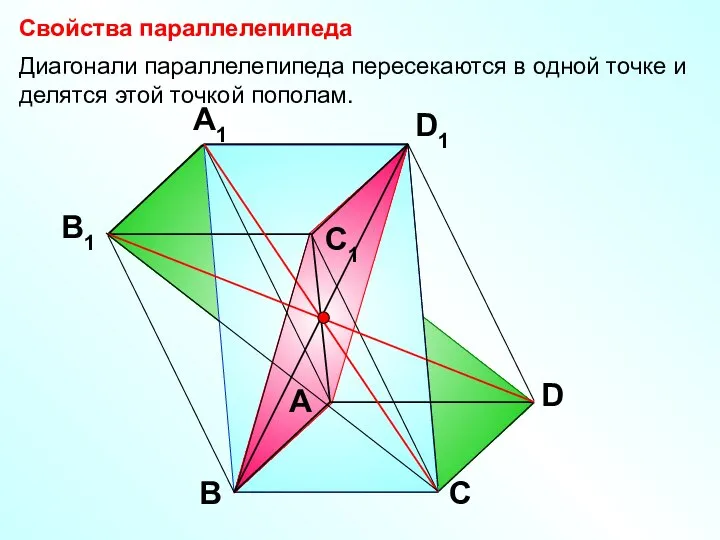
- 12. А В С D D1 С1 A1 B1 Свойства параллелепипеда Диагонали параллелепипеда пересекаются в одной точке
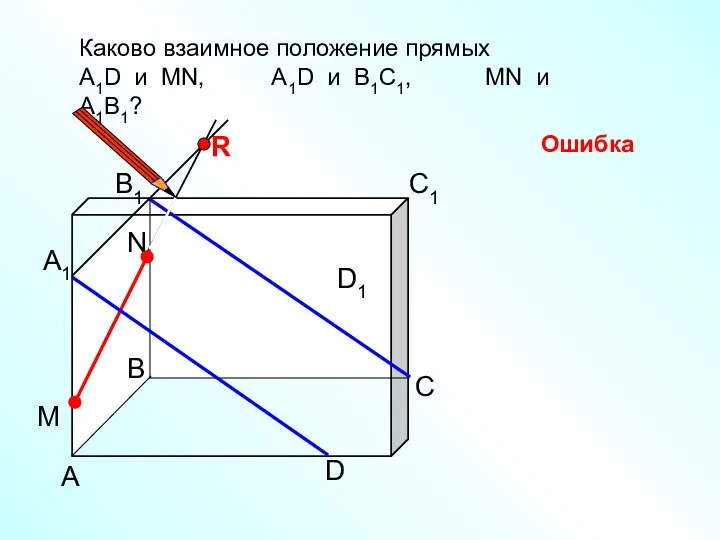
- 13. А D С В B1 С1 D1 А1 Каково взаимное положение прямых А1D и MN, А1D
- 14. А D С В B1 С1 D1 А1 F E F и E - средины ребер
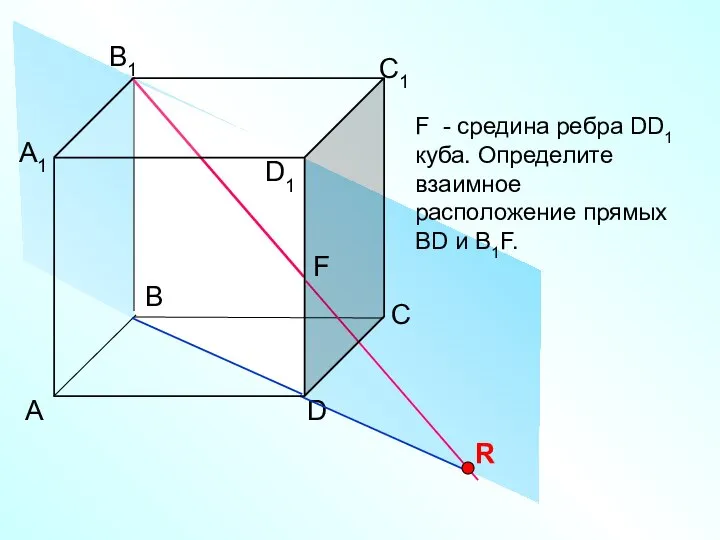
- 15. А D С В B1 С1 D1 А1 F F - средина ребра DD1 куба. Определите
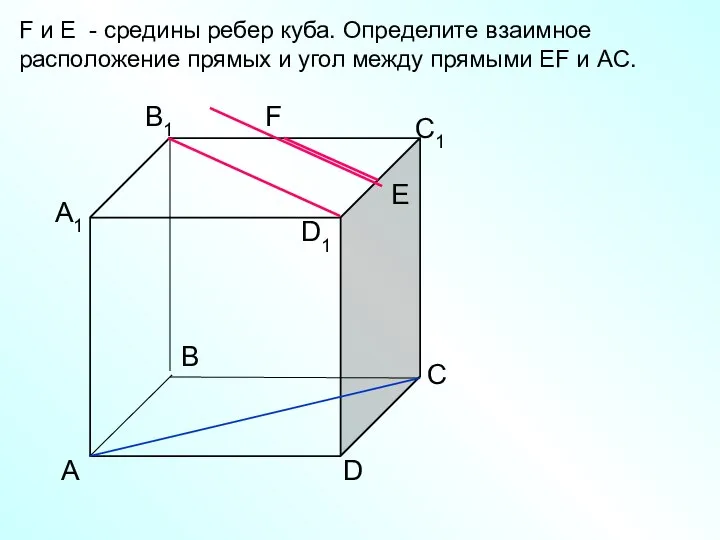
- 16. А D С В B1 С1 D1 А1 F E F и E - средины ребер
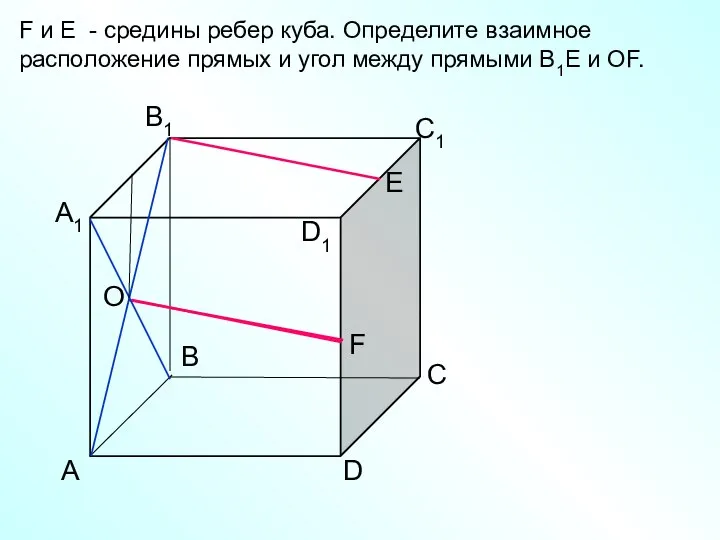
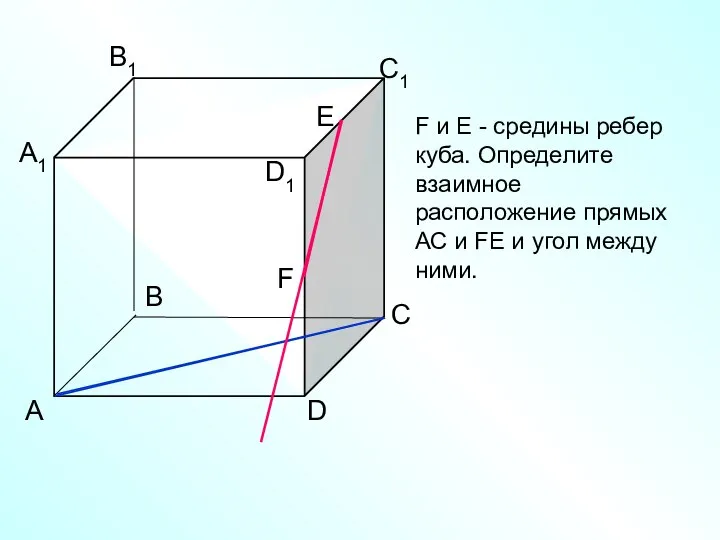
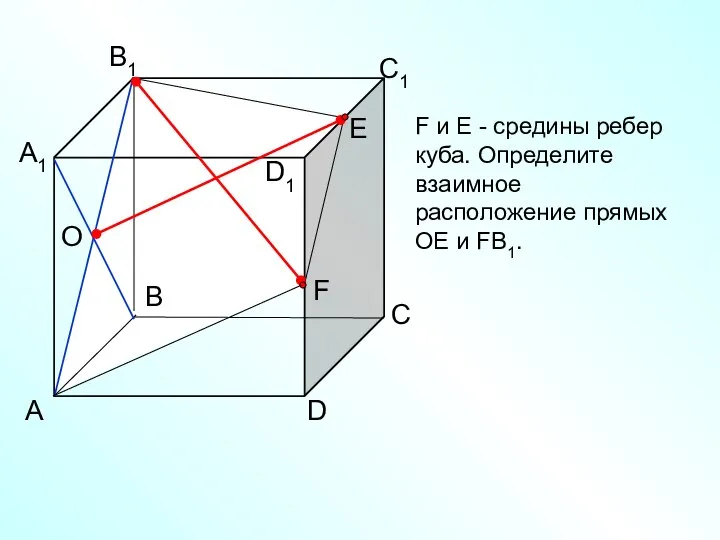
- 17. А D С В B1 С1 D1 А1 F F и Е - средины ребер куба.
- 18. А D С В B1 С1 D1 А1 F F и Е - средины ребер куба.
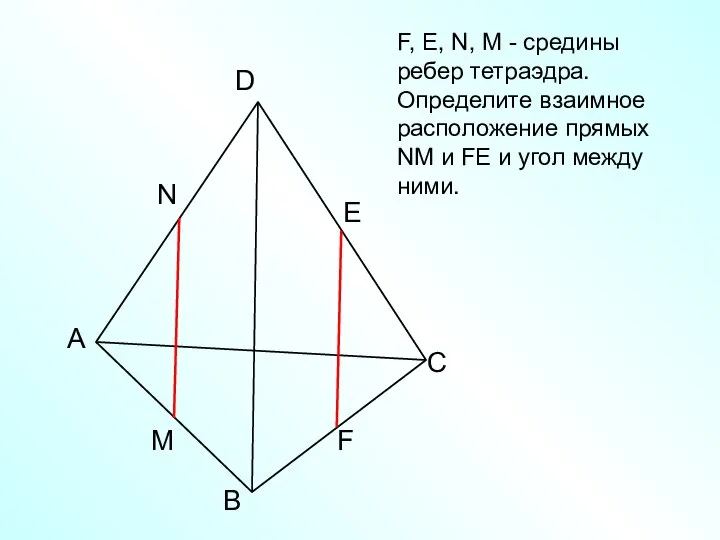
- 19. А В С D N M E F F, Е, N, M - средины ребер тетраэдра.
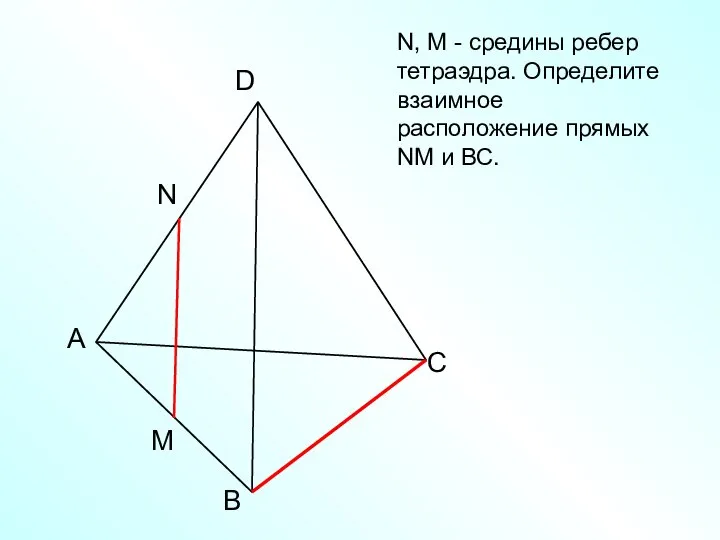
- 20. А В С D N M N, M - средины ребер тетраэдра. Определите взаимное расположение прямых
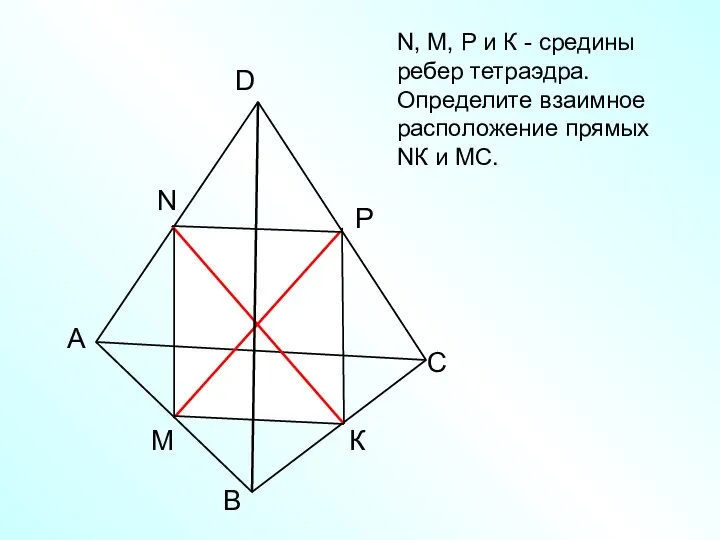
- 21. А В С D N M N, M, Р и К - средины ребер тетраэдра. Определите
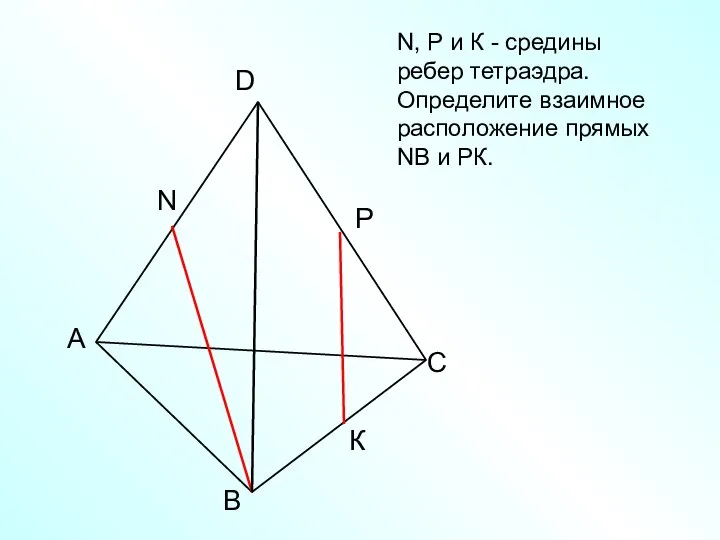
- 22. А В С D N N, Р и К - средины ребер тетраэдра. Определите взаимное расположение
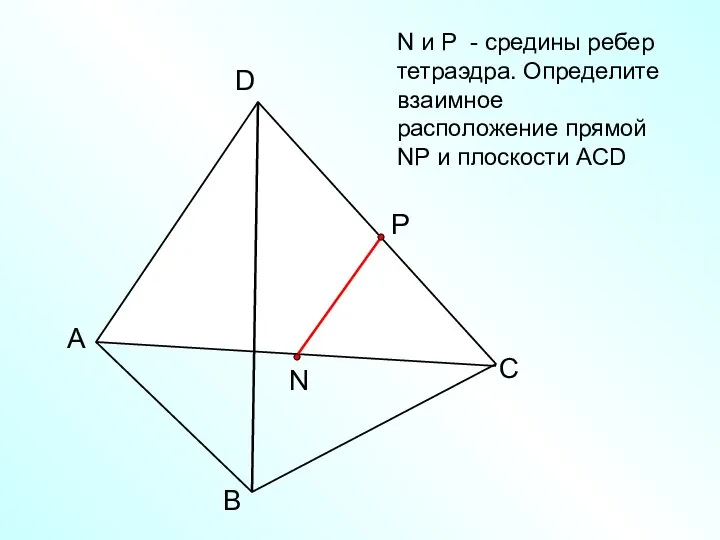
- 23. А В С D N N и Р - средины ребер тетраэдра. Определите взаимное расположение прямой
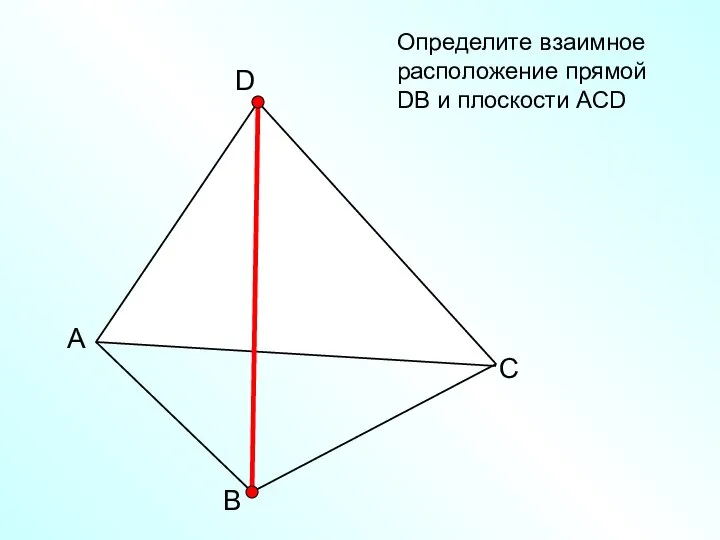
- 24. А В С D Определите взаимное расположение прямой DВ и плоскости АСD
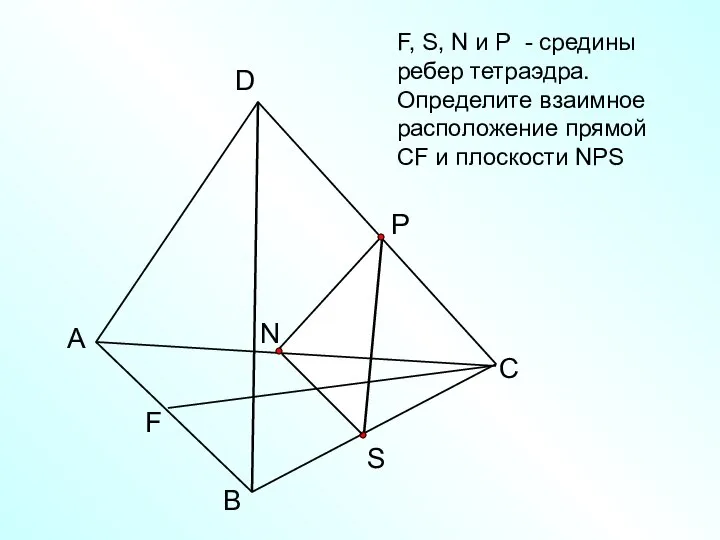
- 25. А В С D N F, S, N и Р - средины ребер тетраэдра. Определите взаимное
- 27. Скачать презентацию
 Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница
Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница Методика изучения площади
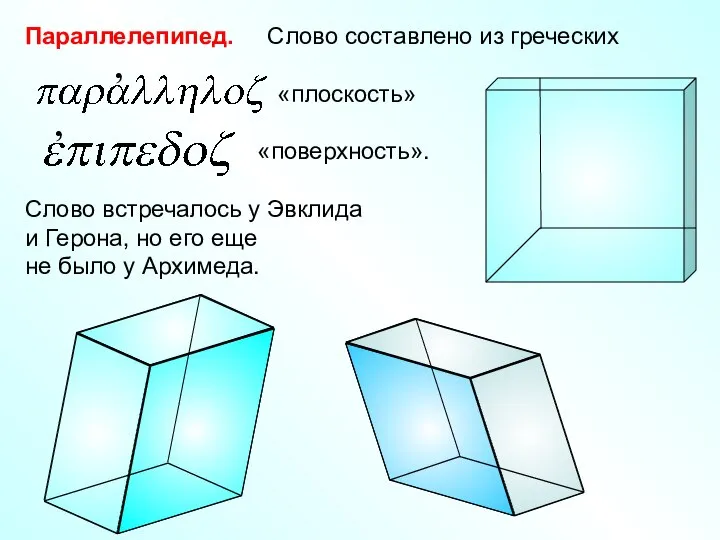
Методика изучения площади Пифагор Самосский
Пифагор Самосский Презентация на тему Методы решения неравенств с одной переменной
Презентация на тему Методы решения неравенств с одной переменной  Презентация на тему Правила дифференцирования
Презентация на тему Правила дифференцирования  Пирамида
Пирамида Параллельные прямые. Подготовка к контрольной работе
Параллельные прямые. Подготовка к контрольной работе Повелеваю в моем сказочном Математическом королевстве ребятам 1-в класса
Повелеваю в моем сказочном Математическом королевстве ребятам 1-в класса Корреляционный анализ
Корреляционный анализ Решение заданий повышенной сложности
Решение заданий повышенной сложности Конструирование предметов из геометрических фигур
Конструирование предметов из геометрических фигур Тренажёр. Таблица умножения
Тренажёр. Таблица умножения Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Všetko o kocke
Všetko o kocke Задачи на готовых чертежах для подготовки к ЕГЭ
Задачи на готовых чертежах для подготовки к ЕГЭ Разложение многочлена на множители
Разложение многочлена на множители Неопределенность измерения. Порядок расчета
Неопределенность измерения. Порядок расчета Приложение производной
Приложение производной Увеличить на... уменьшить на
Увеличить на... уменьшить на pril1
pril1 Логарифм. Свойства логарифмов
Логарифм. Свойства логарифмов График функции y = ax^2 + n
График функции y = ax^2 + n Действия над обыкновенными дробями. Счет и вычисления
Действия над обыкновенными дробями. Счет и вычисления Ряды. Сходимость рядов
Ряды. Сходимость рядов История возникновения геометрии как науки
История возникновения геометрии как науки Организация поточного обучения по математике в МАОУ СОШ МАСТЕРГРАД
Организация поточного обучения по математике в МАОУ СОШ МАСТЕРГРАД Состав числа в пределах 10; Компоненты задачи
Состав числа в пределах 10; Компоненты задачи Геометрический смысл производной
Геометрический смысл производной