Содержание
- 2. OBJECTIVE In the work we study the problem for the case Have a normal form where
- 3. AIM OF WORK The direct study of a formal normal form with the feature type Bogdanov-Takens
- 4. Takens in 1974 for the system of equations of the form got a fairly simple formal
- 5. General( for all cases) the formal normal form was obtained in 2015. This Form looks very
- 6. THEOREM The field is formally equivalent to one of the following fields formal power series. Forms
- 7. DEFINITION Two analytical vector fields in are formally equivalent ,then and only then when there is
- 8. THE FUNCTIONAL EQUATION OF EQUIVALENCE AND THE SCHEME OF REDUCTION TO SYSTEMS OF LINEAR EQUATIONS Objective
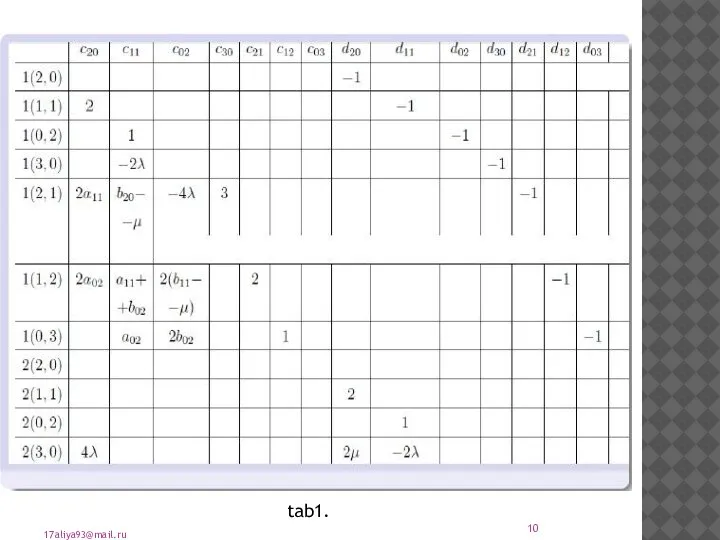
- 9. We substitute the expansions in the main equation : [email protected]
- 10. Get the system of equations. This system has a specific type which allows to solve it
- 11. INFERENCE After we solve this system of equations the formal normal form takes the form We
- 12. REFERENCES Formal normal form Zholandeka Strozhinoy — PWS Publishing, 1997 [email protected]
- 14. Скачать презентацию










 Площади геометрических фигур
Площади геометрических фигур Знакомство с основными понятиями в математике. Задачи с несколькими вопросами
Знакомство с основными понятиями в математике. Задачи с несколькими вопросами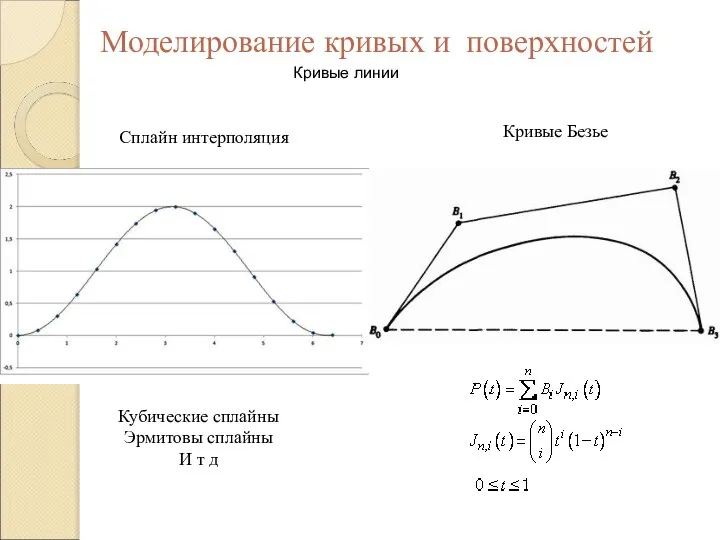 Моделирование кривых и поверхностей
Моделирование кривых и поверхностей Раскрытие скобок
Раскрытие скобок Презентация на тему Транспортир
Презентация на тему Транспортир  Элементы нелинейного функционального анализа. Гладкие многообразия
Элементы нелинейного функционального анализа. Гладкие многообразия Прямоугольник. Квадрат
Прямоугольник. Квадрат Булева алгебра. Классы булевых функций
Булева алгебра. Классы булевых функций Религия Байеса
Религия Байеса Интегральные уравнения
Интегральные уравнения Сравнительный анализ методов полиэдральной аппроксимации при построении гарантирующего решения
Сравнительный анализ методов полиэдральной аппроксимации при построении гарантирующего решения Элементы статистики. Количество звонков в день за ноябрь
Элементы статистики. Количество звонков в день за ноябрь Матрицы и действия над ними
Матрицы и действия над ними Множення і ділення
Множення і ділення Понятие числовой последованности
Понятие числовой последованности Уравнения. Графики
Уравнения. Графики Теорема Пифагора
Теорема Пифагора Правило параллелепипеда
Правило параллелепипеда Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ  Презентация на тему Длина окружности. Площадь круга
Презентация на тему Длина окружности. Площадь круга  Концентрические замощения на основе ромбов Пенроуза
Концентрические замощения на основе ромбов Пенроуза Решение уравнений и неравенств
Решение уравнений и неравенств Сумма углов треугольника
Сумма углов треугольника комбинаторика 1 лекция-1
комбинаторика 1 лекция-1 Начертательная геометрия
Начертательная геометрия Числа 1 – 5 закрепление
Числа 1 – 5 закрепление Как называются числа при вычитании?
Как называются числа при вычитании? Порядок действий
Порядок действий