Концентрические замощения на основе ромбов Пенроуза

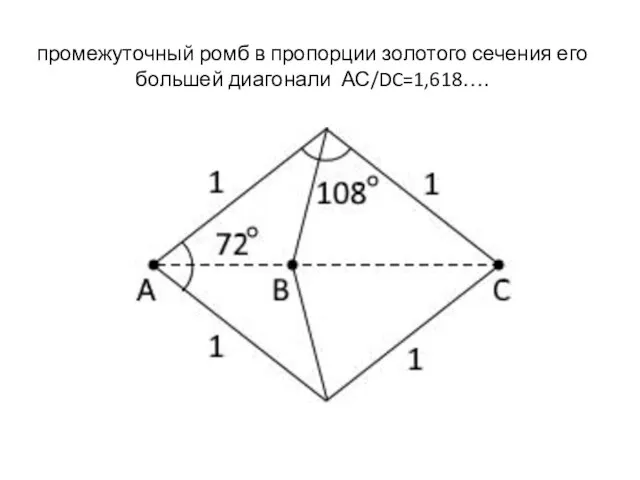
промежуточный ромб в пропорции золотого сечения его большей диагонали АС/DC=1,618….

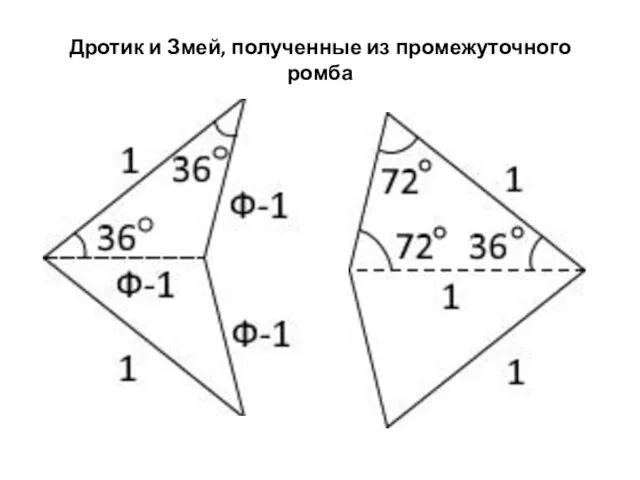
Дротик и Змей, полученные из промежуточного ромба

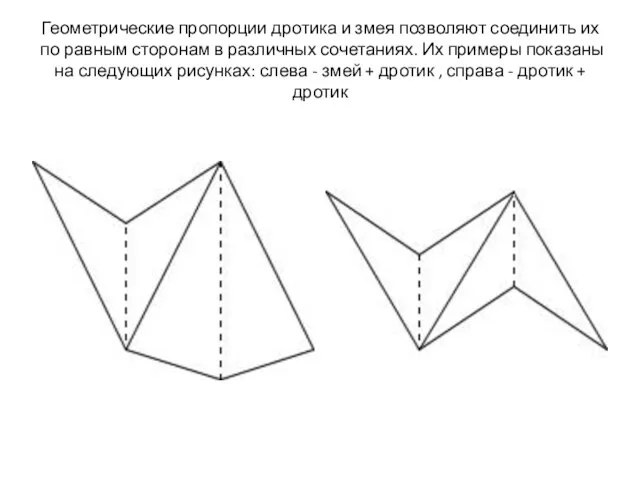
Геометрические пропорции дротика и змея позволяют соединить их по равным сторонам в различных сочетаниях. Их примеры показаны на следующих рисунках: слева - змей + дротик , справа - дротик + дротик

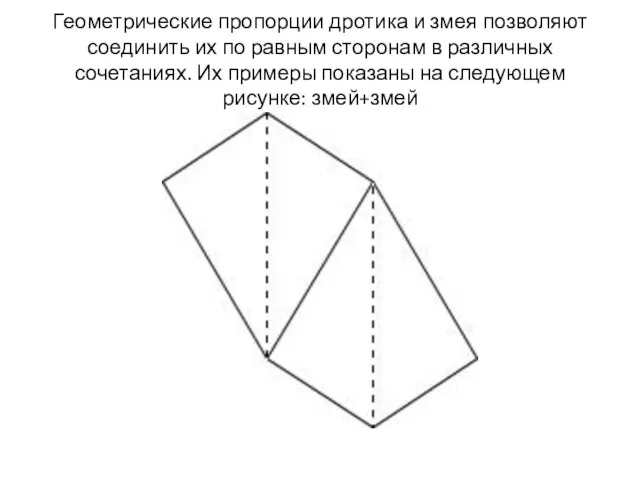
Геометрические пропорции дротика и змея позволяют соединить их по равным сторонам в различных сочетаниях. Их примеры показаны на следующем рисунке: змей+змей

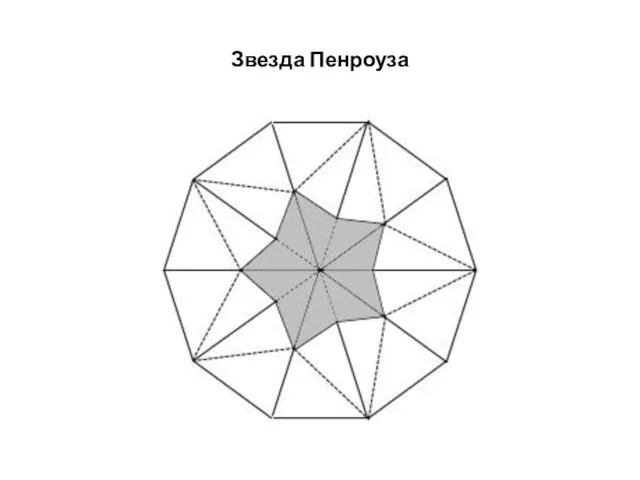
Звезда Пенроуза
На следующем рисунке показана концентрическая мозаика звезда из конгруэнтных дротиков и змеев.
Можно считать, что внутреннюю звезду составляют дротики. Ее внешнее обрамление образуют пары змеев, которые примыкают к дротикам.

Звезда Пенроуза

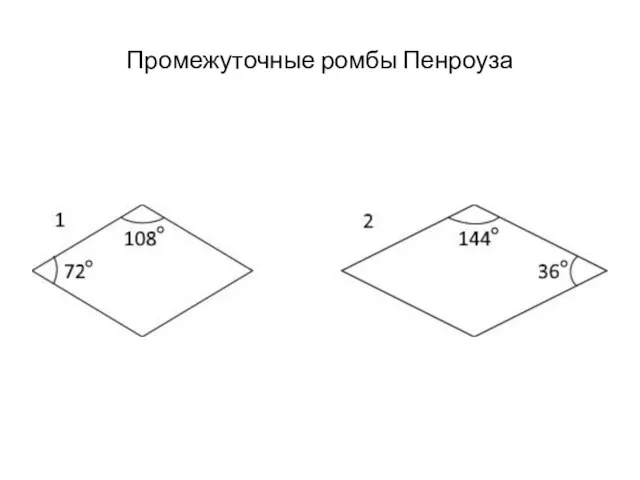
Промежуточные ромбы Пенроуза
Промежуточные ромбы Пенроуза имеют общие стороны со сторонами правильных 5-угольников (см. вводную мозаику Пенроуза), но различаются по углам.
В одном ромбе внутренние углы: 72 и 108 градусов.
В другом ромбе внутренние углы: 36 и 144 градуса.

Промежуточные ромбы Пенроуза

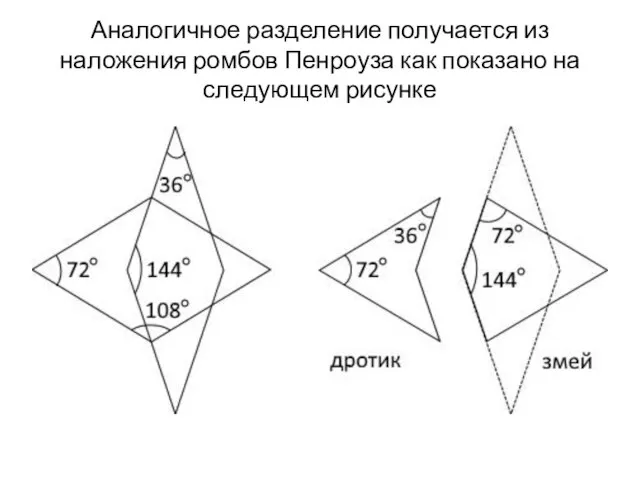
Аналогичное разделение получается из наложения ромбов Пенроуза как показано на следующем рисунке

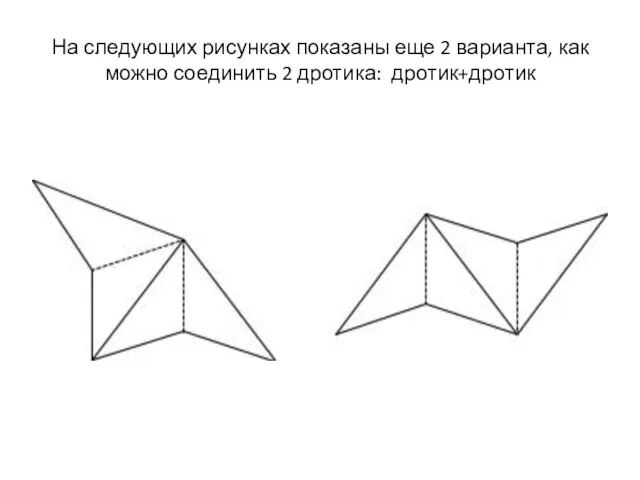
На следующих рисунках показаны еще 2 варианта, как можно соединить 2 дротика: дротик+дротик

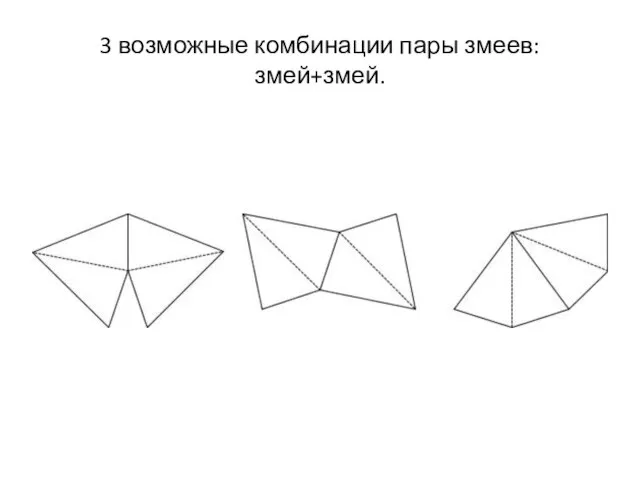
3 возможные комбинации пары змеев: змей+змей.

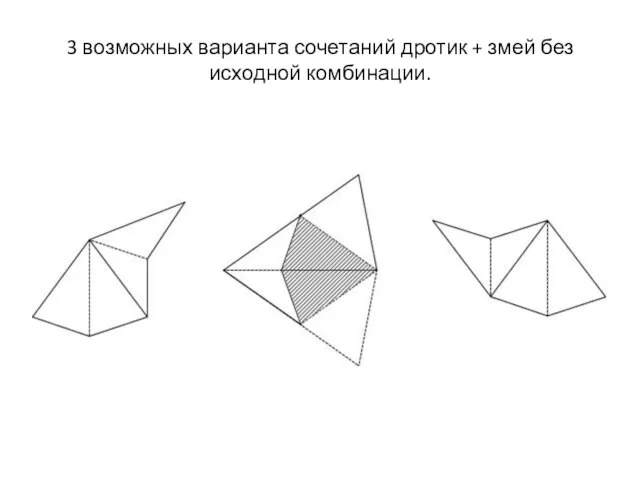
3 возможных варианта сочетаний дротик + змей без исходной комбинации.

КРИВОЛИНЕЙНЫЕ ЗАМОЩЕНИЯ
Это замощения, где грани являются криволинейными многоугольниками или геометрическими фигурами с криволинейными контурами.
Типичным примером криволинейных замощений являются геометрические узоры японских кимоно.
Одна из их разновидностей называется сашико (маленький стежок).
Ее образуют различные сочетания дуг 1/4 окружности на квадратной сетке, сторона любой клетки которой равна радиусу дуги. Когда контур грани образуют 4 дуги 90°, можно составить 24 = 16 выпукло – вогнутых фигур.

6 фигур являются изометрически различными и не могут быть получены друг из друга поворотами и отражениями

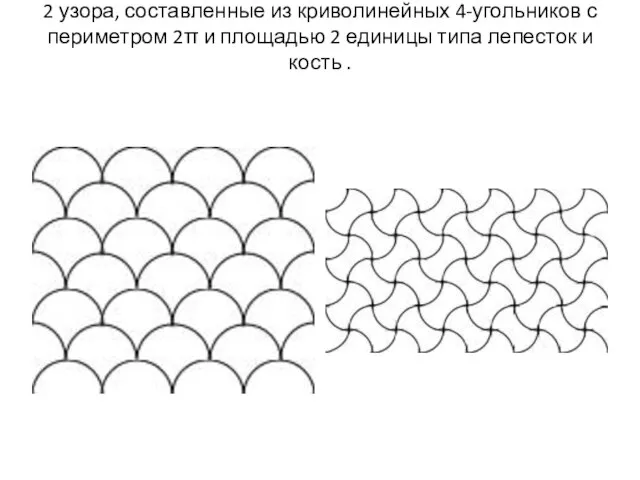
2 узора, составленные из криволинейных 4-угольников с периметром 2π и площадью 2 единицы типа лепесток и кость .

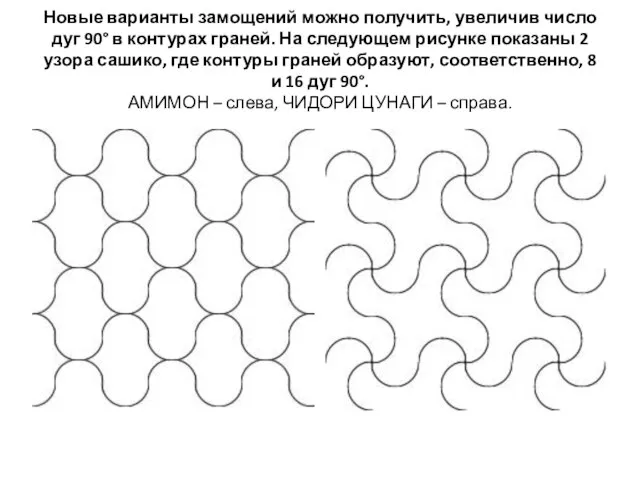
Новые варианты замощений можно получить, увеличив число дуг 90° в контурах граней. На следующем рисунке показаны 2 узора сашико, где контуры граней образуют, соответственно, 8 и 16 дуг 90°.
АМИМОН – слева, ЧИДОРИ ЦУНАГИ – справа.

ЗАМОЩЕНИЕ ПЛОСКИХ ФИГУР
Бесконечное замощение неограниченной плоскости образует конечное число типов граней, которые могут повторяться произвольно много раз. Замощение плоских фигур с конечным размером может быть построено из бесконечного набора однотипных граней, габариты которых образуют монотонно убывающий ряд. Ниже рассмотрено построение бесконечных замощений для прямоугольника и квадрата.
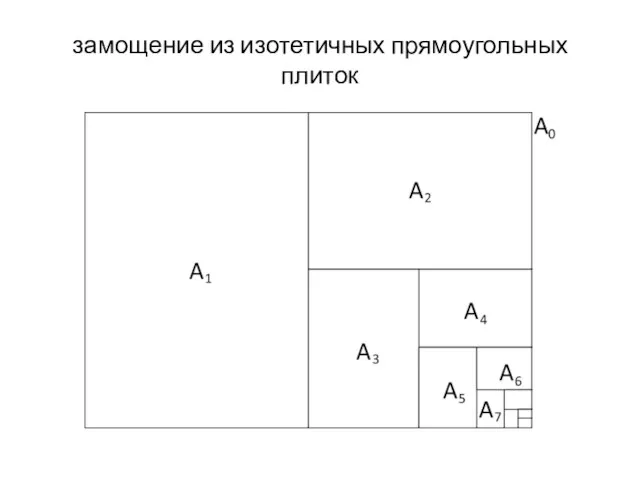
Бесконечное замощение прямоугольника образует следующая последовательность его рекурсивных делений. Сначала исходный прямоугольник нужно разделить по большей стороне на 2 прямоугольника, которые подобны исходному и имеют площадь в 2 раза меньше, чем у него. Аналогичная процедура рекурсивно повторяется с любой (или с каждой) из полученных половин бесконечное число раз. Ограничив глубину рекурсии произвольным можно получить замощение из изотетичных (одинаково расположенных) прямоугольных плиток, стороны которых параллельны сторонам исходного прямоугольника.

замощение из изотетичных прямоугольных плиток

Половинное деление плиток
В технической практике такой принцип половинного деления плиток прямоугольного замощения применен для стандартизации форматов листов чертежей по ГОСТ 2.301-68. для справки размеры и обозначения их основных форматов представлены в следующей таблице.

Половинное деление плиток
Из сравнения размеров и обозначений видно, что основные форматы образуют нормативный ряд, где каждый следующий формат получается делением предыдущего на 2 равные части параллельно меньшей стороне. Цифры обозначения формата показывают кратность его сторон сторонам А4, а их произведения дают число форматов А4, которое нужно для замощения его площади.
Без потери общности можно считать, что площадь исходного прямоугольника (А0) равна 1 (м2). Тогда формальным обоснование конвергенции замощения является равенство 1 суммы площадей его плиток.

Половинное деление плиток
Они образуют бесконечно убывающую геометрическую прогрессию со знаменателем и начальным членом равными 1/2. как видно из следующей формулы ее сумма равна 1:
2- 1+2-2+…+2-n+…= (1/2)/[1-(1/2)]=1.
Для бесконечного замощения квадрата используется следующая техника срединных перпендикуляров сторон. Сначала исходный квадрат делится на 4 равных квадрата перпендикулярами его сторон. Каждый из них также делится на 4 квадрата. Далее аналогичным образом на 4 квадрата делится каждый квадрат текущего внешнего слоя, этот процесс может быть продолжен до бесконечности.

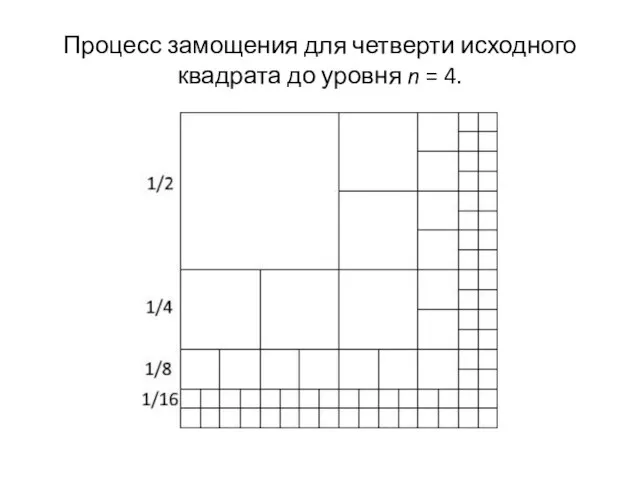
Процесс замощения для четверти исходного квадрата до уровня n = 4.

Метод бесконечного замощения квадратаа
Если считать длину стороны исходного квадрата равной 1, то стороны квадратов замощения образуют бесконечно убывающую последовательность степеней 2, предел которой равен 0, а сумма равна 1 (как для прямоугольного замощения выше), гарантируя сходимость замощения. Его количественными параметрами являются число квадратов по контуру и внутри каждого уровня n. Четверть числа квадратов замощения an по границе каждого уровня n определяют следующие рекуррентные соотношения:
a1 = 1; an+1 = 2·an + 3.

Метод бесконечного замощения квадрата
Чтобы получить итерационную формулу нужно найти сумму разностей соседних элементов рекурсивной последовательности:
a2 – a1 = a1 + 3
+
a3 – a2 = 2(a1 + 3)
+
a4 – a3 = 22(a1 + 3)
+
………………….
+
an – an-1 = 2n-2·(a1 + 3)
_______________________________
an – a1 = (1 + 2 + 22 + … + 2n-2)(a1 +3)

Метод бесконечного замощения квадрата
С учетом значения суммы (n – 2) последовательных степеней 2 и а1 = 1 получается следующая формула числа квадратов канта n каждой четверти этого квадратного замощения:
an = (2n-1 – 1)(1 + 3) +1 = 2n+1 – 3.
Например, в каждой четверти на уровне n = 4 по этой формуле получается 29 квадратов.
a4 = 24+1 – 3 = 29.
Общее число квадратов в каждой четверти до уровня n дает сумма Sn этих значений от 1 до n. В результате опять получается сумма последовательных степеней 2, но со смещением 3 и начиная с 22, как видно из следующего соотношения:
Sn = a1 + … + an = (2n+2 – 1) – 3n – (20 + 21) = 2n+2 – 3n – 4.