Содержание
- 3. Цель – исследовать влияние пятого постулата Евклида на развитие математики 19 и 20 века. Задачи: раскрыть
- 4. «Геометрия Лобачевского (гиперболическая геометрия) — очень хитрое математическое колдунство по типу всем известной геометрии Евклида, но
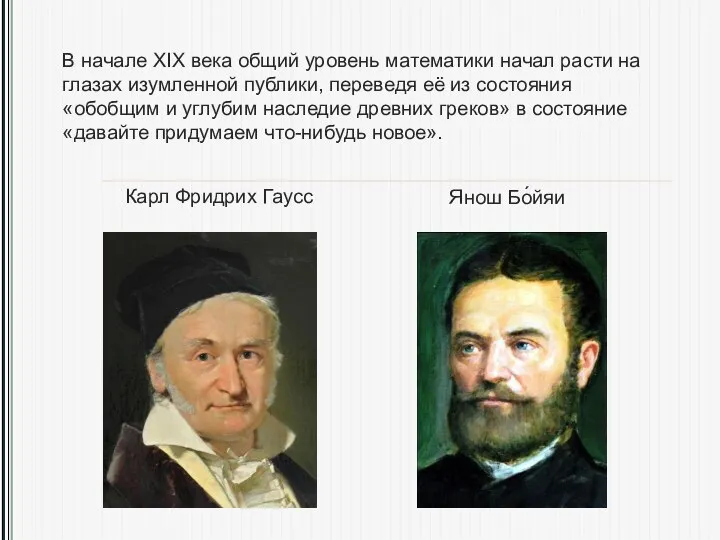
- 5. В начале XIX века общий уровень математики начал расти на глазах изумленной публики, переведя её из
- 6. Карл Фридрих Гаусс - «Король математиков» не оставил без внимания «пятый постулат» евклидовой геометрии. Он пришел
- 7. Янош Бо́йяи уже в колледже настолько увлёкся исследованием пятого постулата Евклида, что отец – математик с
- 8. Классический постулат Евклида (5-я аксиома геометрии): В плоскости через точку, не лежащую на данной прямой, можно
- 9. Геометрия Лобачевского вполне доступна для понимания. Идея отказаться от одной аксиомы в пользу другой не кажется
- 10. В 1829 году вышла первая работа Лобачевского по неевклидовой геометрии. Основная проблема была в том, что
- 11. Признание к Лобачевскому пришло только после смерти, когда другие математики придумали наглядные модели для его геометрии.
- 12. Работы Николая Ивановича и прочих борцов за неевклидовость во многом перевернули математику как науку. Родились новые
- 14. Скачать презентацию









 Домашнее задание. Решение задач
Домашнее задание. Решение задач Векторы на плоскости
Векторы на плоскости Случаи вычитания 11-
Случаи вычитания 11- Знакомство с основными понятиями в математике. Задачи с несколькими вопросами
Знакомство с основными понятиями в математике. Задачи с несколькими вопросами Древнекитайское доказательство
Древнекитайское доказательство Пределы
Пределы История теоремы Пифагора
История теоремы Пифагора Построение сечений многогранников
Построение сечений многогранников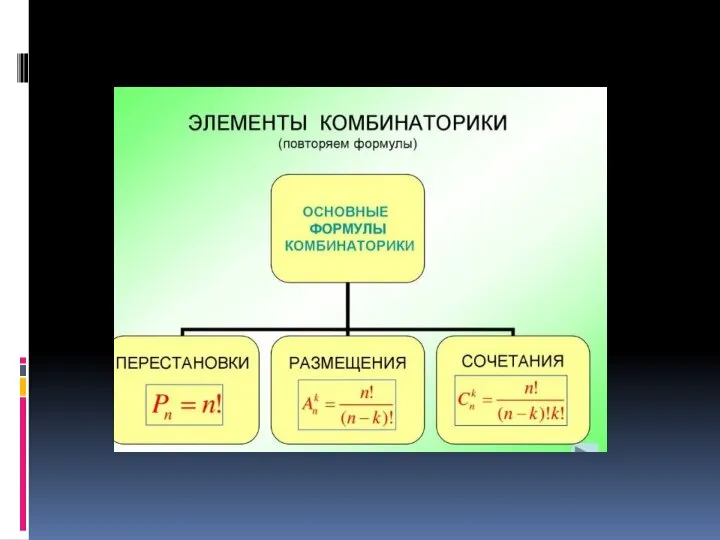 Основные понятия комбинаторики
Основные понятия комбинаторики предел_числ_посл
предел_числ_посл Стереометрия. Многогранники
Стереометрия. Многогранники Отношения и пропорции. Золотое сечение
Отношения и пропорции. Золотое сечение Площади и объемы
Площади и объемы Частные производные. Полный дифференциал функции
Частные производные. Полный дифференциал функции Многоугольники
Многоугольники Многочлены с несколькими переменными и их стандартный вид
Многочлены с несколькими переменными и их стандартный вид Кусочная функция
Кусочная функция Символика и терминология. Системы координат. Лекция 1
Символика и терминология. Системы координат. Лекция 1 Презентация на тему Слагаемое сумма
Презентация на тему Слагаемое сумма  Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Презентация на тему Нумерация в пределах 1000
Презентация на тему Нумерация в пределах 1000  Призма. Понятие и чертёж
Призма. Понятие и чертёж 1_2_opredeliteli (1)
1_2_opredeliteli (1) Центральная симметрия
Центральная симметрия Домашнее задание . Подготовка к контрольной работе
Домашнее задание . Подготовка к контрольной работе Решение задач на кратное сравнение чисел
Решение задач на кратное сравнение чисел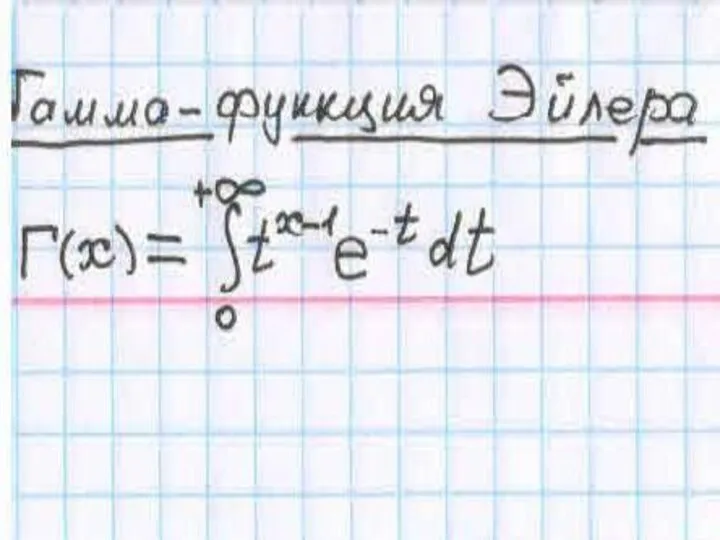 Гамма-функция Эйлера
Гамма-функция Эйлера