Содержание
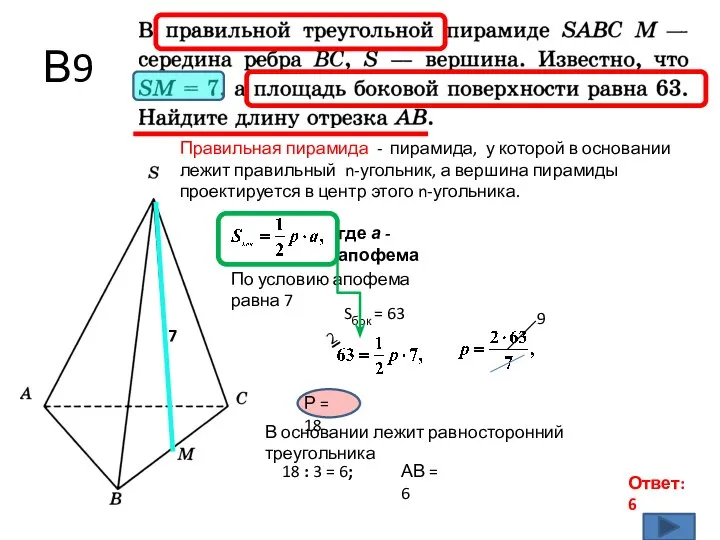
- 2. В9 Ответ: 6 Правильная пирамида - пирамида, у которой в основании лежит правильный n-угольник, а вершина
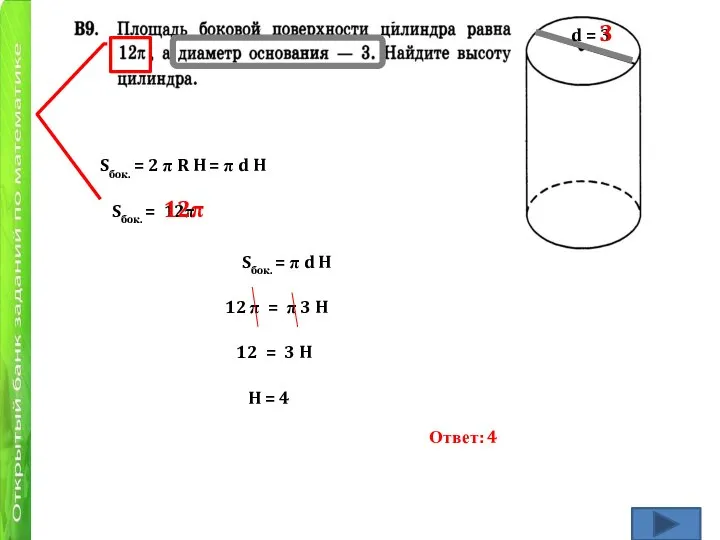
- 3. Sбок. = 2 π R H = π d H d = 3 Sбок. = 12π
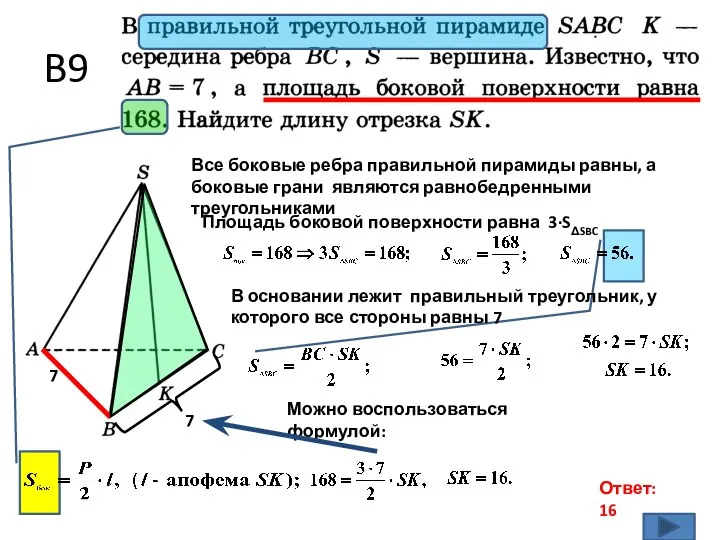
- 4. B9 Ответ: 16 7 Все боковые ребра правильной пирамиды равны, а боковые грани являются равнобедренными треугольниками
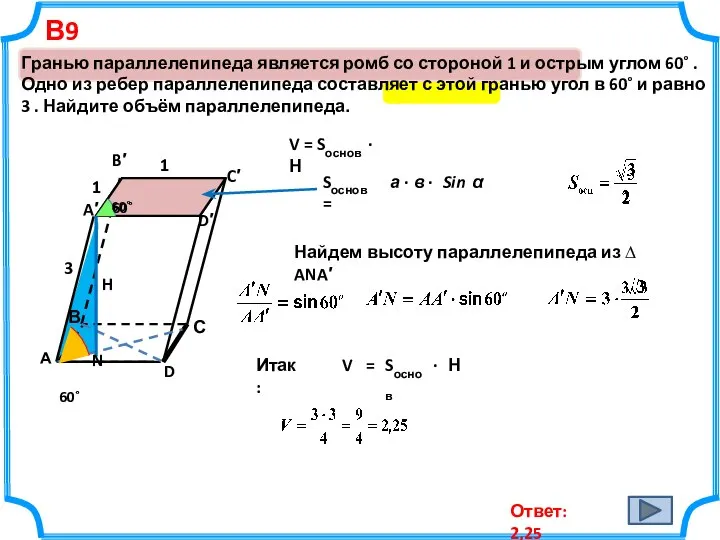
- 5. В9 Гранью параллелепипеда является ромб со стороной 1 и острым углом 60˚ . Одно из ребер
- 6. В10 Ответ: 0,1 Число благоприятных исходов – это N(A) = 1 (по вызову придет желтое такси).
- 7. Всего 150 возможных исходов. Благоприятен исход, когда купленный фонарик окажется исправным. Таких благоприятных исходов 150 –
- 8. B10 Ответ: 0,4 При двукратном бросания игрального кубика может выпасть: (5,1); (1,5); (2,4); (4,2); (3,3) Итак
- 9. а а а а Н 3а 3а 3а 3а 3Н От перестановки мест сомножителей произведение не
- 10. B11 Ответ: 6 d 384см 8d Тогда площадь основания увеличилась в 64 раз. Объем цилиндра равен
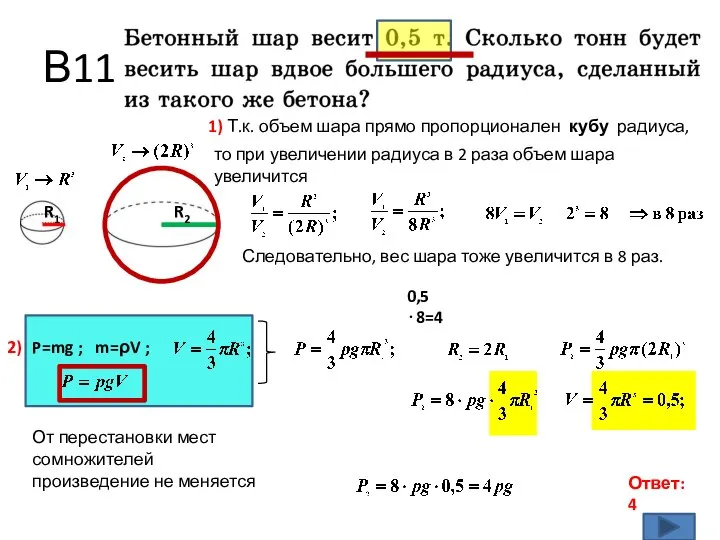
- 11. В11 Ответ: 4 1) Т.к. объем шара прямо пропорционален кубу радиуса, P=mg ; m=ρV ; то
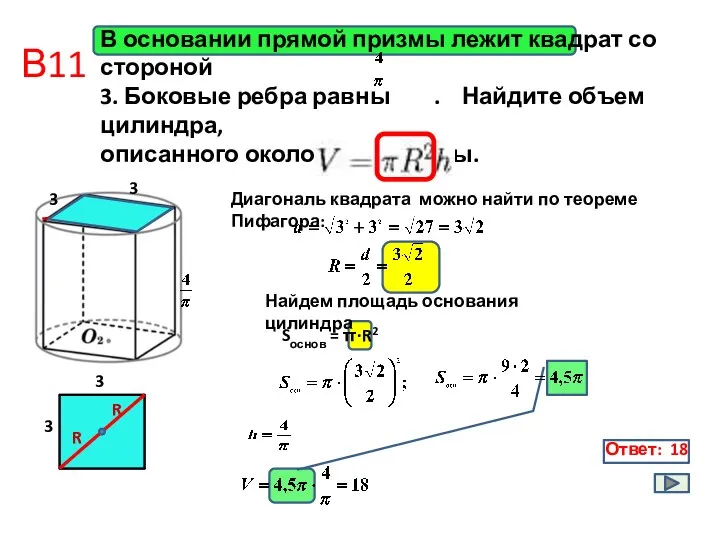
- 12. В11 Ответ: 18 В основании прямой призмы лежит квадрат со стороной 3. Боковые ребра равны .
- 14. Скачать презентацию





 Прибавить и вычесть число 3. Решение текстовых задач
Прибавить и вычесть число 3. Решение текстовых задач Презентация на тему Золотое сечение - гармония математики
Презентация на тему Золотое сечение - гармония математики  Свойства числовых функций
Свойства числовых функций Логарифм числа и его свойства
Логарифм числа и его свойства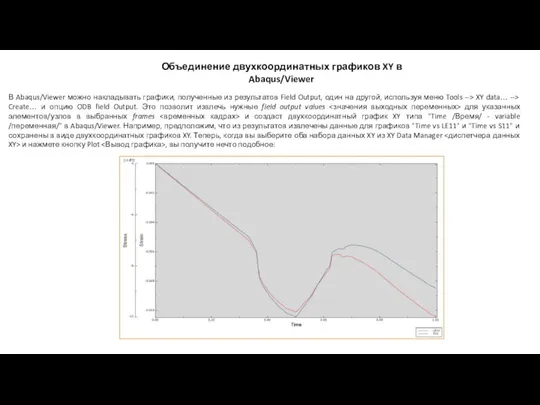 Объединение двухкоординатных графиков XY в Abaqus/Viewer
Объединение двухкоординатных графиков XY в Abaqus/Viewer Повторюємо арифметичні дії множення і ділення
Повторюємо арифметичні дії множення і ділення Устный счёт
Устный счёт Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց)
Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց) Уравнения с параметром
Уравнения с параметром Действия со смешанными числами
Действия со смешанными числами Разбор типового расчета по статистике
Разбор типового расчета по статистике Путешествие в страну дроби
Путешествие в страну дроби Геометрический калейдоскоп
Геометрический калейдоскоп Математическая игра Счастливое число 7!
Математическая игра Счастливое число 7! Интегральное исчисление
Интегральное исчисление Методика обучения математике и ее предмет
Методика обучения математике и ее предмет Окружность. Элементы окружности
Окружность. Элементы окружности Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Логические задачи. 1 класс
Логические задачи. 1 класс Движение. Виды движения
Движение. Виды движения Дидактическая игра. Веселый ёжик
Дидактическая игра. Веселый ёжик Násobíme a delíme s Mimoňmi
Násobíme a delíme s Mimoňmi Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Пересечение поверхностей
Пересечение поверхностей Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Дискретная математика с элементами математической логики. Основы теории множеств
Дискретная математика с элементами математической логики. Основы теории множеств Викторина по математике, 1 класс
Викторина по математике, 1 класс