Содержание
- 2. Цели урока: Повторение, обобщение и проверка знаний по теме «Треугольники», выработка основных навыков.
- 3. Хочешь научиться плавать,- смело входи в воду! Хочешь научиться решать задачи,- решай их!
- 4. Задача №1. Используя данные, указанные на рисунке, найдите катет ST. 1) 5 3) 4) Ответ: 3.
- 5. Задача №2. Используя данные, указанные на рисунке, найдите катет ST. 9 2) 3) 4) Ответ: 3.
- 6. Задача №3. Используя данные, указанные на рисунке, найдите площадь прямоугольного треугольника. 156 78 60 30 Ответ:
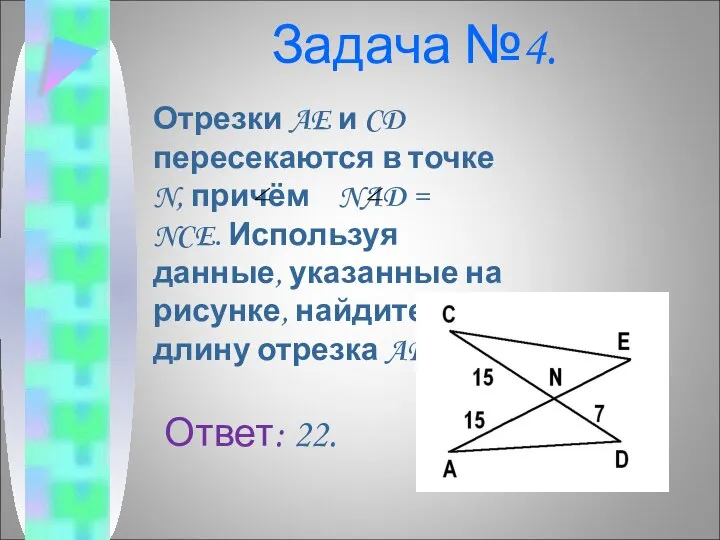
- 7. Задача №4. Отрезки AE и CD пересекаются в точке N, причём NAD = NCE. Используя данные,
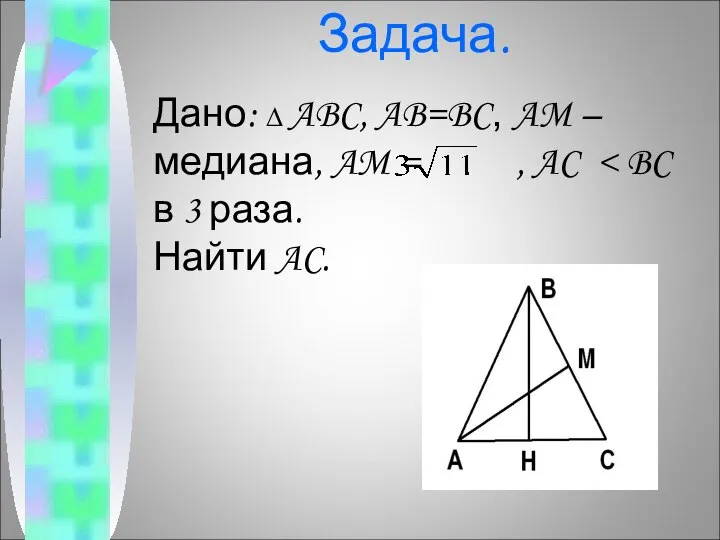
- 8. Задача. Дано: ∆ ABC, AB=BC, AM – медиана, AM = , AC Найти AC.
- 9. Способ 1. Пусть AC = x , AB = BC = 3x . Отложим на луче
- 10. Способ 2. Обозначим AC = 2x , тогда AH = CH = x , BC =
- 11. 1) Биссектриса всегда делит пополам один из углов треугольника. 2) Биссектрисы произвольного треугольника точкой пересечения делятся
- 12. Три пути ведут к знанию: путь размышления- самый благодарный, путь подражания- самый лёгкий и путь опыта-
- 14. Скачать презентацию









 Куб. Длина, ширина, высота
Куб. Длина, ширина, высота Теория вероятностей, подготовка к ЕГЭ - 2019
Теория вероятностей, подготовка к ЕГЭ - 2019 Параллельность прямых
Параллельность прямых Презентация на тему Первый признак равенства треугольников
Презентация на тему Первый признак равенства треугольников  Системы уравнений
Системы уравнений ЕГЭ. Производная в заданиях уровня В. 2 часть
ЕГЭ. Производная в заданиях уровня В. 2 часть Гласные звуки и буквы. Слова с буквой Э
Гласные звуки и буквы. Слова с буквой Э Тригонометрические уравнения
Тригонометрические уравнения Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Геометрическая прогрессия
Геометрическая прогрессия Площадь прямоугольника
Площадь прямоугольника Неравенства с двумя переменными и их системы
Неравенства с двумя переменными и их системы Алгебра. 7 класс
Алгебра. 7 класс Статистика. Обработка данных
Статистика. Обработка данных Неопределенный интеграл. Способы вычисления
Неопределенный интеграл. Способы вычисления Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат
Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат Сравнение натуральных чисел
Сравнение натуральных чисел Понятие множества и подмножества
Понятие множества и подмножества Принципы статистического оценивания. Анализ данных
Принципы статистического оценивания. Анализ данных Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна.
Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна. Презентация на тему Параллельные прямые, треугольники
Презентация на тему Параллельные прямые, треугольники  概率论与数理统计
概率论与数理统计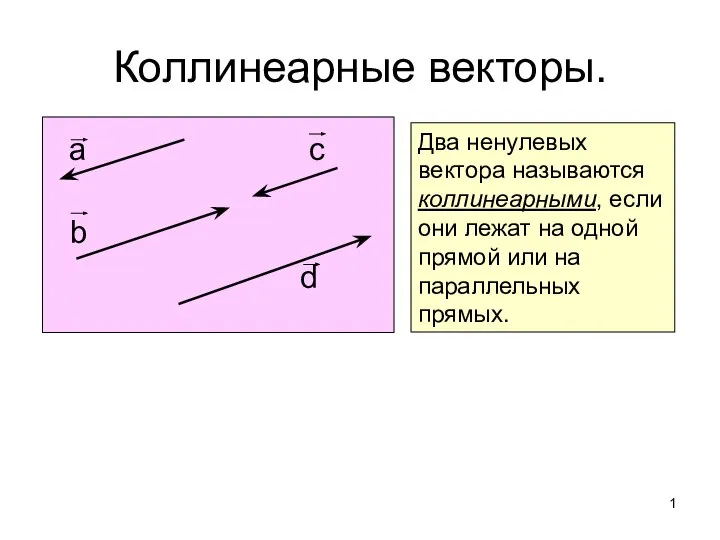 Коллинеарные векторы
Коллинеарные векторы Методы решения типовых задач по специальной теории относительности
Методы решения типовых задач по специальной теории относительности Расстояния и углы
Расстояния и углы Перпендикулярность плоскостей
Перпендикулярность плоскостей Основы дисперсионного анализа
Основы дисперсионного анализа Экономическая статистика. Демография предприятий
Экономическая статистика. Демография предприятий