Содержание
- 2. ТРИГОНОМЕТРИЯ – (от греч. trigwnon – треугольник и metrew – измеряю) – математическая дисциплина, изучающая зависимости
- 3. Дополнил и систематизировал различные случаи решения плоских и сферических треугольников Открыл «плоскую» теорему косинусов и формулы
- 4. Ввел понятие функции и принятую в наши дни символику Разъяснил вопрос о знаках всех тригонометрических функций
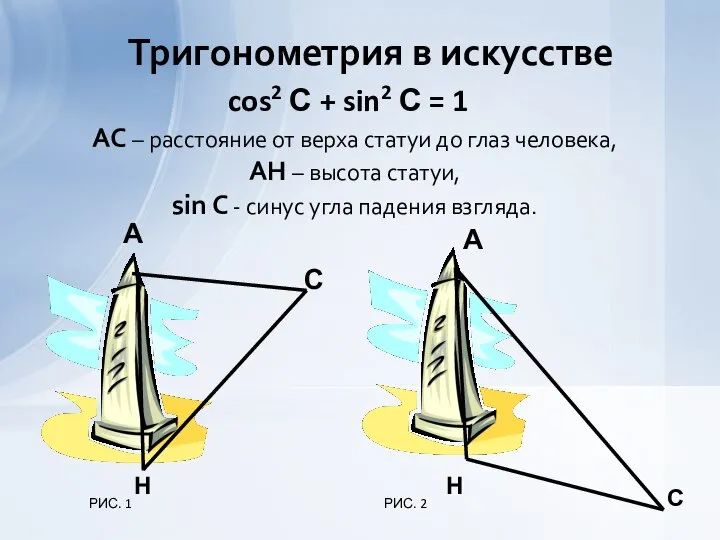
- 5. С А Н РИС. 1 С РИС. 2 Н cos2 С + sin2 С = 1
- 6. Разработал метод проектирования сложных форм в 1920 году; Выразил тригонометрические функции как отношение координат x, y,
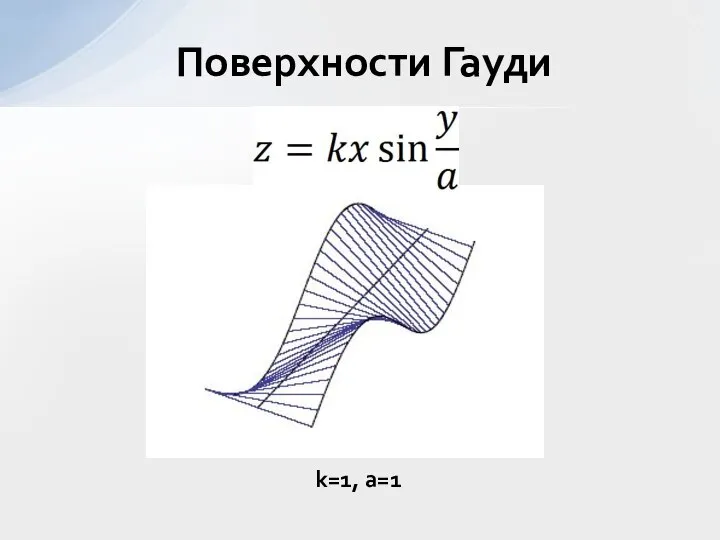
- 7. Поверхности Гауди k=1, a=1
- 8. Детская школа Гауди в Барселоне
- 9. Страховая корпорация Swiss Re в Лондоне x = λ y = f(λ)cos θ z = f(λ)sin
- 10. Сантьяго Калатрава Винодельня «Бодегас Исиос»
- 11. Феликс Кандела Ресторан в Лос-Манантиалесе [adcos(t) + ddt , bdsin(t), cdt + edt2]
- 12. Готическая архитектура Собор Парижской Богоматери 1163г. – середина XIV века.
- 13. Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), называются гармоническими
- 14. n1 - показатель преломления первой среды n2 - показатель преломления второй среды α-угол падения, β-угол преломления
- 15. Ка́устика — геометрическое место всех фокусов негомоцентрических пучков
- 16. 1. Сферическая капля 2. Внутреннее отражение 3. Первичная радуга 4. Преломление 5. Вторичная радуга 6. Входящий
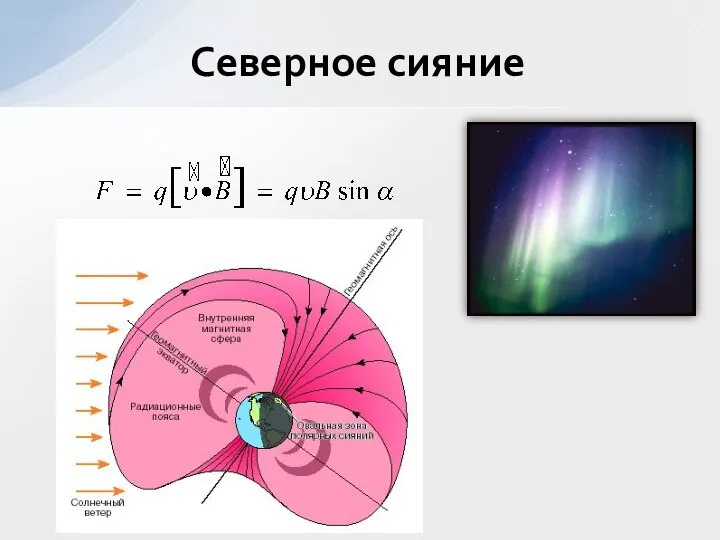
- 17. Северное сияние
- 18. Тригонометрия в биологии
- 19. Бета-ритм - 14-30 Гц, активная умственная деятельность Альфа-ритм – 8-13 Гц, монотонная, рутинная деятельность Тета-ритм –
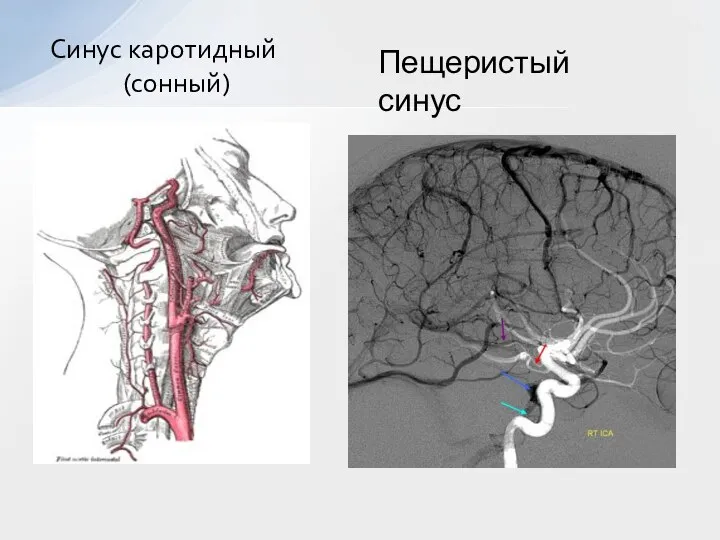
- 20. Синус каротидный (сонный) Пещеристый синус
- 22. Скачать презентацию







![Феликс Кандела Ресторан в Лос-Манантиалесе [adcos(t) + ddt , bdsin(t), cdt + edt2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1121470/slide-10.jpg)







 Состав чисел первого десятка
Состав чисел первого десятка Отрезок. Сравнение отрезков
Отрезок. Сравнение отрезков Занимательная математика
Занимательная математика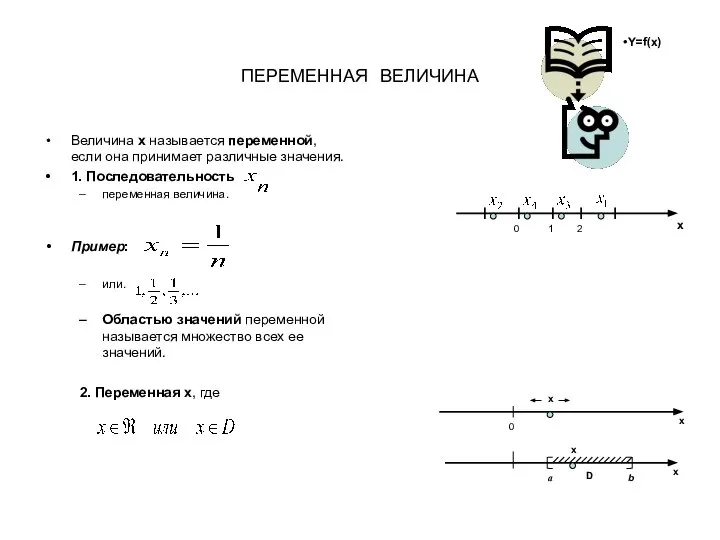 Переменная величина
Переменная величина Интересное о математике
Интересное о математике Понятие логарифма
Понятие логарифма Устный счёт. Закрепление изученного
Устный счёт. Закрепление изученного Определители
Определители Таблица умножения трёх
Таблица умножения трёх Множество. Элемент множества
Множество. Элемент множества Логические схемы
Логические схемы Игры. Памятка
Игры. Памятка Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Цилиндр. Конус
Цилиндр. Конус Випадкова подія. Відносна частота події. Імовірність події
Випадкова подія. Відносна частота події. Імовірність події Решение тригонометрических уравнений
Решение тригонометрических уравнений Презентация по математике "Логарифмическая функция. Преобразования графиков." -
Презентация по математике "Логарифмическая функция. Преобразования графиков." -  Интервальные оценки
Интервальные оценки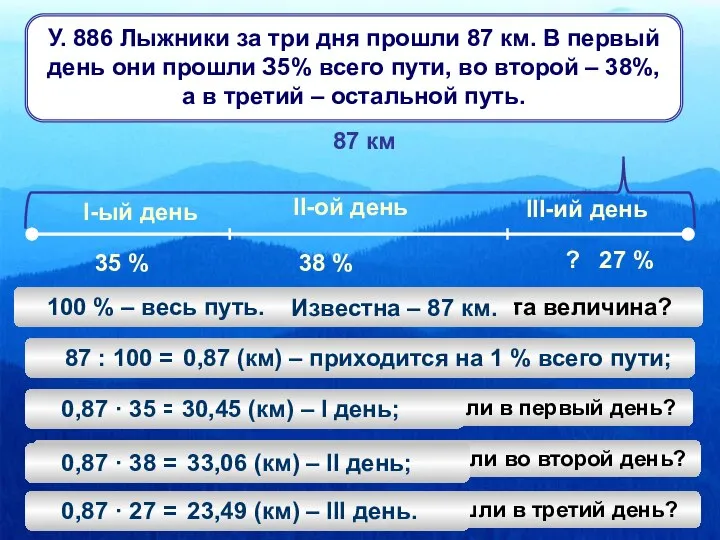 Задачи о лыжниках
Задачи о лыжниках Окружность. Проверочная работа
Окружность. Проверочная работа ГИА - 2016. Задачи №9,10,11,12
ГИА - 2016. Задачи №9,10,11,12 Решение уравнений и неравенств. Линейные уравнения и неравенства
Решение уравнений и неравенств. Линейные уравнения и неравенства Уравнение окружности
Уравнение окружности Тригонометрические уравнения
Тригонометрические уравнения Решение задач с помощью чертежа
Решение задач с помощью чертежа Арифметические действия с дробями
Арифметические действия с дробями Вписанная окружность
Вписанная окружность Задачи на концентрацию, сплавы. Подготовка к ЕГЭ
Задачи на концентрацию, сплавы. Подготовка к ЕГЭ