Трикутники

Мета :
1. Домогтися засвоєння учнями змісту понять “трикутник”; ”сторони, кути , вершини”, “кут, протилежний стороні”, “кут, прилеглий до сторони”, “рівні трикутники” та ознак рівності трикутників.
2. Формувати уміння учнів розпізнавати та називати елементи трикутників, зображених на рисунку .
3. Розвивати логічне мислення, уяву, математичну мову учнів.
4. Розв'язувати задачі на обчислення сторін трикутника за відомим периметром і навпаки, та задачі на доведення, використовуючи ознаки рівності трикутників.

Зміст
Історична довідка
Трикутник і його елементи
Класифікація трикутників за сторонами і кутами.
Рівність трикутників (ознаки рівності трикутників)
Співвідношення між сторонами і кутами трикутника. Нерівність трикутників
Рівнобедрений трикутник ( ознаки та властивості рівнобедреного трикутника)
Прямокутний трикутник
Сума кутів трикутника

Трикутник – найпростіша фігура: три вершини й три сторони. Але під час вивчення трикутника утворилася окрема наука - тригонометрія, у якій метричні властивості трикутника виражаються через функції його кутів. Ця наука виникла на основі практичної необхідності у вимірюванні ділянок, складанні карт місцевості, конструюванні машин і механізмів.
Перші відомості про трикутник та його властивості ми знаходимо в єгипетських папірусах, яким більше 4000 років. У них зокрема, згадується спосіб знаходження площі рівнобедреного трикутника.
Через 2000 років у Стародавній Греції вивчення властивостей трикутника досягає високого рівня.
У XV—XVI ст. з'явилася величезна кількість досліджень властивостей трикутника, які ввійшли в розділ планіметрії, що одержав назву «Нова геометрія трикутника».
Великий внесок у розвиток геометрії трикутника внесли мате­матики XIX—XX ст.: Лемуан, Брокар, Тебо й ін.
Історична довідка

Трикутник і його елементи
Нехай А, В, С - три довільні точки, які не лежать на одній прямій.
Фігура, яка складається із трьох відрізків АВ, ВС, АС (рис. 1), називається трикутником ABC (позначається: Δ ABC).
Трикутником також називають частину площини, обмежену відрізками АВ, ВС, АС (плоский трикутник).
Точки А, В, С - вершини, відрізки АВ, ВС, АС - сторони трикутника.
Сума довжин усіх сторін трикутника називається його периметром.
Рис. 1

Кутом (або внутрішнім кутом) трикутника ABC при вершині А називається кут, утворений променями АВ і АС. Аналогічно визначаються кути трикутника при вершинах В і С.
Кути CAB, ABC, ВСА трикутника ABC часто позначають однією буквою (А, В, С відповідно) або грецькими буквами α, β, γ (при цьому всередині кутів зображують дуги, див. рис. 1). Говорять, що кут А протилежний стороні ВС або сторона ВС протилежна куту А; аналогічно кут В і сторона АС, кут С і сторона ВА протилежні.
Кут, суміжний з будь-яким кутом трикутника, називається зовнішнім кутом цього трикутника. Наприклад, кут BCD (рис. 2) - зовнішній. При кожному куті трикутника можна побудувати по два зовнішніх кути (продовживши одну чи другу сторону кута). Ці два кути рівні як вертикальні.
Рис. 2

Бісектрисою трикутника називається відрізок, який зєднує вершину трикутника з точкою на протилежній стороні і ділить внутрішній кут навпіл. (рис. 3).
Позначають l.
Бисектриса ділить протилежну сторону на частини , пропорційні прилеглим сторонам: ab : ac = b : c
Бисектриса ділить площу трикутника, пропорційно прилеглим сторонам.
Довільний трикутник має три бісектриси.
Рис. 3

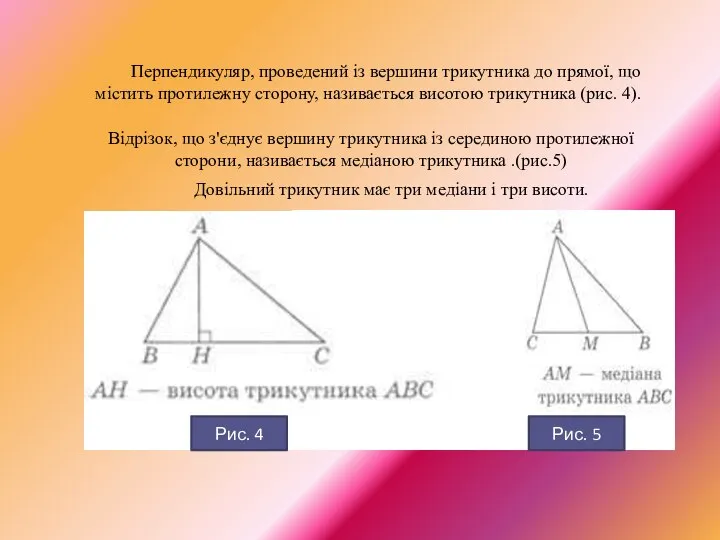
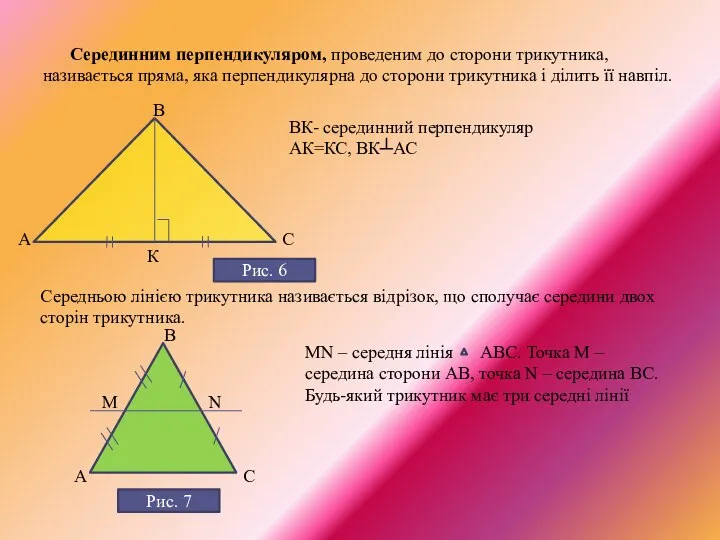
Відрізок, що з'єднує вершину трикутника із серединою протилежної сторони, називається медіаною трикутника .(рис.5)
Перпендикуляр, проведений із вершини трикутника до прямої, що містить протилежну сторону, називається висотою трикутника (рис. 4).
Довільний трикутник має три медіани і три висоти.
Рис. 4
Рис. 5

Серединним перпендикуляром, проведеним до сторони трикутника, називається пряма, яка перпендикулярна до сторони трикутника і ділить її навпіл.
А
Середньою лінією трикутника називається відрізок, що сполучає середини двох сторін трикутника.
В
С
К
ВК- серединний перпендикуляр
АК=КС, ВК┴АС
А
В
С
N
M
MN – середня лінія АВС. Точка M – середина сторони АВ, точка N – середина ВС.
Будь-який трикутник має три середні лінії
Рис. 6
Рис. 7

Класифікація трикутників за сторонами і кутами.
Залежно від кількості рівних сторін розрізняють рівносторонні, рівнобедрені і різносторонні трикутники.
Трикутник, дві сторони якого рівні, називається рівнобедреним (АС = ВС на рисунку 8, а). Третя сторона - основа, рівні сторони – бічні сторони.
Трикутник, три сторони якого рівні (АС = ВС = АВ на рис. 8, б), називається рівностороннім трикутником.
Трикутник в якого всі сторони мають різну довжину, називається різностороннім трикутником. (рис. 9)
Рис. 8
Рис. 9

Залежно від величини кутів розрізняють гострокутні, тупокутні і прямокутні трикутники.
Прямокутним називається трикутник в якого один кут прямий, тобто дорівнює 900 , а два інші кути гострі. У прямокутному трикутнику сторона, яка лежить проти прямого кута, називається гіпотенузою, дві інші сторони – катетами (рис.10, а).
Тупокутним називається трикутник, в якого один кут тупий, тобто більший від 900 і менший від 1800 , а два інші кути є гострі (рис. 10, б).
Гострокутним називається трикутник, у якого всі три кути гострі, тобто менші за 900 (рис. 10, в).
Рис. 10

Два трикутники називаються рівними, якщо вони суміщаються при накладанні.
На рисунку 11 зображено рівні трикутники ABC і А1В1С1.
Кожен із цих трикутників можна накласти на інший так, що вони повністю сумістяться, тобто попарно сумістяться їх вершини і сторони. Ясно, що при цьому сумістяться попарно і кути цих трикутників.
Рівність трикутників
(ознаки рівності трикутників)
Рис. 11

Таким чином, якщо два трикутники рівні, то елементи (тобто сторони і кути) одного трикутника відповідно дорівнюють елементам другого трикутника.
Відмітимо, що в рівних трикутниках проти відповідно рівних сторін (тобто тих, що суміщаються при накладанні) лежать рівні кути, і, навпаки, проти відповідно рівних кутів лежать рівні сторони.
Так, наприклад, у рівних трикутниках ABC і А1В1С1, зображених на рисунку 11, проти відповідно рівних сторін АВ і A1B1 лежать рівні кути С і С1. Рівність трикутників ABC і А1В1С1 позначають: Δ АВС = Δ А1В1С1.
Рівність двох трикутників можна встановити, порівнюючи деякі їх елементи.
Перша ознака рівності трикутників
ТЕОРЕМА. Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.
Рис. 12

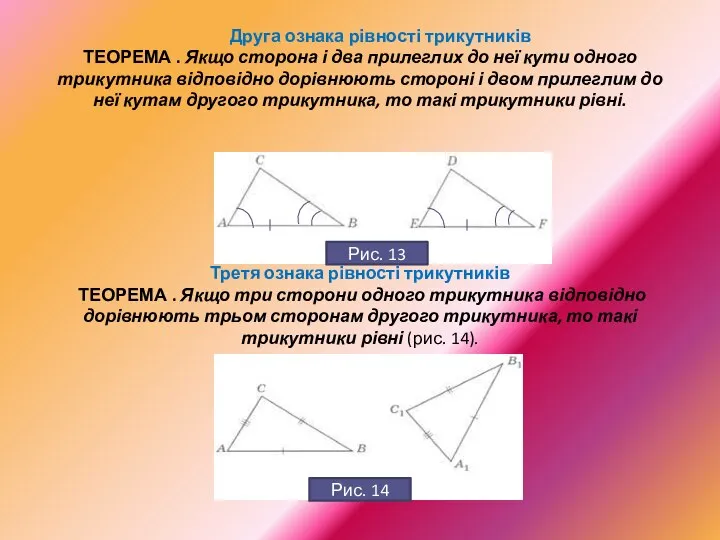
Друга ознака рівності трикутників
ТЕОРЕМА . Якщо сторона і два прилеглих до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам другого трикутника, то такі трикутники рівні.
Третя ознака рівності трикутників
ТЕОРЕМА . Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам другого трикутника, то такі трикутники рівні (рис. 14).
Рис. 13
Рис. 14

ТЕОРЕМА . У трикутнику проти більшої сторони лежить більший кут
Із теореми випливає
Наслідок . Якщо два кути трикутника рівні, то трикутник рівнобедрений (ознака рівнобедреного трикутника).
З наслідку випливає: якщо три кути трикутника рівні, то трикутник рівносторонній.
ТЕОРЕМА . У трикутнику проти більшого кута лежить більша сторона.
З теореми одержуємо
Наслідок . У прямокутному трикутнику гіпотенуза більша, ніж катет.
ТЕОРЕМА . Кожна сторона трикутника менша від суми двох інших сторін.
Наслідок . Для довільних трьох точок, А, В і С, що не лежать на одній прямій, справедливі нерівності:
АВ < АС + СВ, АС < АВ + ВС, ВС < ВА + АС.
Кожна з цих нерівностей називається нерівністю трикутника.
Співвідношення між сторонами і кутами трикутника.
Нерівність трикутників

Рівнобедрений трикутник (влвстивості та ознаки трикутника)
Трикутник, дві сторони якого рівні, називається рівнобедреним. Третя сторона - основа, рівні сторони – бічні сторони.
Властивості рівнобедреного трикутника
У рівнобедреному трикутнику кути при основі рівні.
У рівнобедреному трикутнику бісектриса, проведена до основи, є його медіаною і висотою.
У рівнобедреному трикутнику висоти проведені до бічних сторін , рівні.
У рівнобедреному трикутнику медіани проведені до бічних сторін , рівні.
У рівнобедреному трикутнику бісектриси кутів при основі рівні.
Рінобедрений трикутник має одну вісь симетрії.
Ознаки рівнобедреного трикутника
Якщо в трикутнику два кути рівні, то він рівнобедрений.
Якщо в трикутнику медіана є бісектрисою і висотою, то він рівнобедрений.
Якщо трикутник має одну вісь симетрії, то він рівнобедрений.

Прямокутним називається трикутник в якого один кут прямий, тобто дорівнює 900 , а два інші кути гострі. У прямокутному трикутнику сторона, яка лежить проти прямого кута, називається гіпотенузою, дві інші сторони – катетами.
Ознаки рівності прямокутних трикутників
Якщо катети одного прямокутного трикутника відповідно дорівнюють катетам другого прямокутного трикутника, то такі трикутники рівні.
Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету і прилеглому до нього гострому куту другого прямокутного трикутника, то такі трикутники рівні.
Якщо гіпотенуза і гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі і гострому куту другого прямокутного трикутника, то такі трикутники рівні.
Якщо гіпотенуза і катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі і катету другого прямокутного трикутника, то такі трикутники рівні.
Прямокутний трикутник
Рис. 15

Якщо катет і прилежний йому гострий кут одного прямокутного трикутника відповідно дорівнюють катету і протилежному йому гострому куту другого прямокутного трикутника, то такі трикутники рівні.
Властивості прямокутних трикутників
Сума гострих кутів прямокутного трикутника дорівнює 900.
Гіпотенуза прямокутного трикутника більша за кожного з катетів.
Катет прямокутного трикутника, що лежить проти кута 300, дорівнює половині гіпотенузи.
Властивості катетів , медіан і висот прямокутного трикутника
Катет прямокутного трикутника є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу.
Висота прямокутного трикутника, проведена з вершини прямого кута, є середнім пропорційним між проекціями катетів на гіпотенузу.
Висота прямокутного трикутника, проведена з вершини прямого кута, виражається через сторони і проекції катетів.
Медіана прямокутного трикутника, проведена з вершини прямого кута, дорівнює половині гіпотенузи.

ТЕОРЕМА
Сума кутів трикутника дорівнює 180°.
Доведення.
Розглянемо довільний трикутник ABC і покажемо, що ∠A + ∠B + ∠C = 180°.
Проведемо через вершину В пряму а, паралельну стороні АС (рис. 16). Кути 1 і 4 є різносторонніми кутами при перетині паралельних прямих а і АС січною АВ, а кути 3 і 5 - різносторонніми кутами при перетині тих же паралельних прямих січною ВС. Тому
∠ 4 = ∠ 1, ∠ 5 = ∠ 3. (1)
Сума кутів трикутника.
Рис. 16

Очевидно, сума кутів 4, 2 і 5 дорівнює розгорнутому куту з вершиною В, тобто
∠ 4 + ∠ 2 + ∠ 5 = 180°.
Звідси, враховуючи рівності (1), одержимо: ∠ 1 + ∠ 2 + ∠ 3 = 180°, або ∠A + ∠B + ∠C = 180°.
Теорему доведено.
Наслідки.
1) Сума гострих кутів прямокутного трикутника дорівнює 90°.
2) У рівнобедреному прямокутному трикутнику кожен гострий кут дорівнює 45°.
3) У рівносторонньому трикутнику кожен кут дорівнює 60°.
4) У довільному трикутнику або всі кути гострі, або два кути гострі, а третій тупий або прямий.
5) Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним.
Доведення. З рівності ∠ 4 + ∠ 3 = 180° і ∠ 1 + ∠ 2 + ∠ 3 = 180° (рис. 17) одержуємо, що ∠ 4 = ∠ 1 + ∠ 2.
Рис. 17

Дана презентація створена до теми “ТРИКУТНИКИ”, яка вивчається у 7 класі на уроках геометрії в ІІ семестрі. Кожен слайд презентації можна використовувати на уроках геометрії, щоб учні краще засвоювали програмний матеріал.
На дану тему відводиться 18 годин.
Презентацію підготовила:
вчитель математики Матусець Т.М.